(单词翻译:单击)
选择题部分(共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设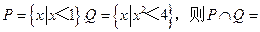
(A)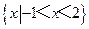 (B)
(B)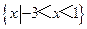
(C)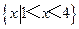 (D)
(D)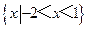
答案D
【命题意图】本题考查集合运算,需先求出集合Q的具体的范围,然后求交集.
【解析】由题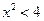 ,所以
,所以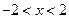 ,所以
,所以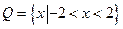 ,所以
,所以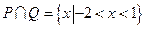 ,故选D.
,故选D.
(2)已知函数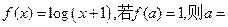
(A)0(B)1(C)2(D)3
答案B
【命题意图】本题主要考查对数的基本运算,直接利用已知条件中的等量关系求解.
【解析】由题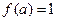 ,得到
,得到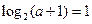 ,解得
,解得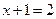 ,所以
,所以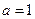 ,故选B.
,故选B.
(3)设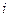 为虚数单位,则
为虚数单位,则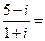
(A)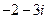 (B)
(B)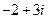 (C)
(C)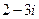 (D)
(D)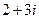
答案C
【命题意图】本题主要考查复数的基本运算,属于容易题.
【解析】由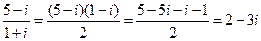 ,故选C.
,故选C.
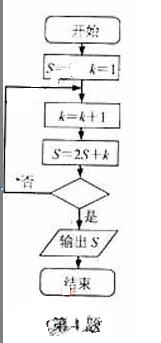
(4)某程度框图如图所示,若输出的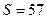 ,则判断框内为
,则判断框内为
(A)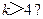 (B)
(B)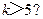
(C)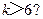 (D)
(D)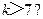
答案A
【命题意图】本题考查程序框图的有关知识,同时考查识图、用图能力.
【解析】由题开始k=k+1=1+1=2,s=2×1+2=4,不满足条件需继续循环,则k=k+1=2+1=3,s=2×4+3=11,k=k+1=3+1=4,s=2×11+4=26,k=k+1=4+1=5,s=2×26+5=57,此时满足条件,应输出S,所以判断框内应为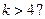 ,故选A.
,故选A.
(5) 设
设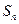 为等比数列
为等比数列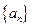 的前n项和,
的前n项和,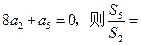
(A)-11(B)-8(C)5(D)11
(A)-11(B)-8(C)5(D)11
答案A
【命题意图】本题考查等比数列的基本运算.
【解析】由题数列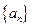 为等比数列,
为等比数列,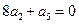 ,即
,即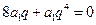 ,因为
,因为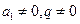 ,所以有
,所以有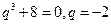 ,
,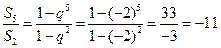 ,故选A.
,故选A.
(6)设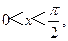 则“xsin2 x<1”是“xsin x<1”的
则“xsin2 x<1”是“xsin x<1”的
(A)充分而不必要条件(B)必要而不充分条件
(C)充分必要条件(D)既不充分也不必要条件
答案B
【命题意图】本题主要考查充要条件的判断.
【解析】因为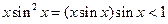 ,
,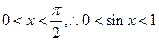 ,不一定能推出
,不一定能推出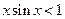 成立,但当
成立,但当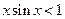 成立时,因为
成立时,因为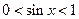 ,所以有
,所以有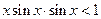 ,即
,即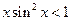 ,一定成立.故选
,一定成立.故选 B.
B.
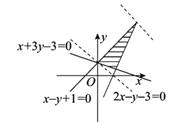
(7)若实数x、y满足不等式组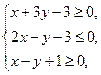 则x+y的最大值为
则x+y的最大值为
(A)9(B)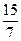
(C)1 (D)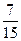
答案A
【命题意图】本题考查线性规划的有关最值问题,利用已知条件画出可行域求解.
【解析】已知约束条件形成的可行域如图所示当目标函数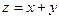 过
过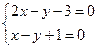 的交点
的交点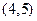 点时取得最大值为9,故选A.
点时取得最大值为9,故选A.
(8)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是
(A)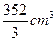 (B)
(B)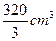
(C)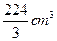 (D)
(D)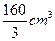
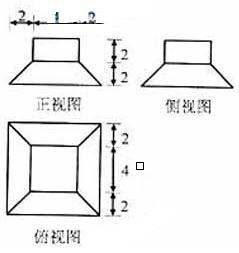
答案B
【命题意图】本题主要考查空间几何体的三视图及利用三视图求解几何体的体积等知 识.
识.
【解析】由三视图可知,该几何体是由一个正四棱柱和一个正四棱台组合形成的,由图中数据可知四棱柱的体积为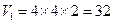 ,
,
底层正四棱台的体积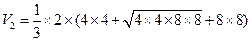
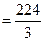 ,所以该组合体的体积为
,所以该组合体的体积为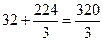 ,故选B.
,故选B.
(9)已知x0是函数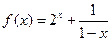 的一个零点,若
的一个零点,若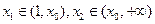 ,则
,则
(A)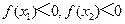 (B)
(B)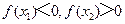
(C)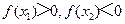 (D)
(D)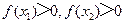
9.答案B
【命题意图】本题主要考查函数的零点问题及函数的单调性的判断.
【解析】由题可知已知函数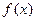 是由函数
是由函数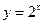 与
与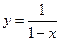 组合而成的,因为两个函数在
组合而成的,因为两个函数在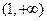 上均为增函数,所以
上均为增函数,所以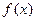 也是
也是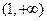 上的增函数,又因为
上的增函数,又因为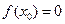 ,
,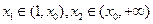 ,所以有函数的草图可知,
,所以有函数的草图可知,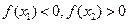 ,故选B.
,故选B.
(10)设O为坐标原点,F1,F2是双曲线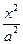 -
-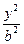 =1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1P F2=60°,
=1(a>0,b>0)的焦点,若在双曲线上存在点P,满足∠F1P F2=60°,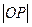 =
=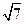 a,
a, 则该双曲线的渐近线方程为
则该双曲线的渐近线方程为
(A)x±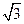 y=0(B)
y=0(B)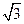 x±y=0
x±y=0
(C) x±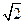 y=0(D)
y=0(D) 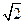 x±y=0
x±y=0
10.答案D
【命题意图】本题主要考查双曲线定义,余弦定理的应用,属于难题.
【解析】由题设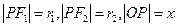 ,则由双曲线的定义可知
,则由双曲线的定义可知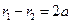 ①,在
①,在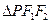 中由余弦定理可得
中由余弦定理可得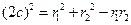 ,②
,②
在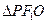 中,
中,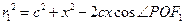 ,③
,③
在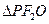 中,
中,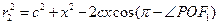 ④
④
由以上四式消掉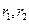 即可求出
即可求出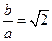 ,可知选D.
,可知选D.
非选择题部分(共100 分)
分)
二、填空题:本大题共7小题,每小题4分,共28分。
(11)在如图所示的茎叶图中,甲、乙两组数据的中位数分别是 , .

11.答案45,46
【命题意图】本题主要考查茎叶图的有关知识.
【解析】由题甲的数据分别为28、31、39、42、45、55、57、58、66,其中位 数为45,乙的数据为29、34、35、42、46、48、53、55、67,其中位数为46.
数为45,乙的数据为29、34、35、42、46、48、53、55、67,其中位数为46.
(12)函数f(x)=sin2 (2x-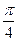 )的最小正周期是 .
)的最小正周期是 .
答案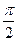
【命题意图】本题主要考查三角恒等变换及三角函数的最小正周期.
【解析】由题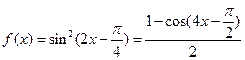
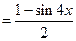 ,所以最小正周期为
,所以最小正周期为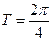
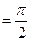 .
.
(13)已知平面向量α,β,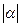 =1,
=1, 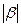 =2,α⊥(α-2β),则
=2,α⊥(α-2β),则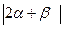 的值是 .
的值是 .
13.答案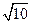
【命题意图】本题主要考查平面向量的基本运算.
【解析】由题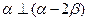 ,所以有
,所以有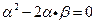 ,因为
,因为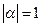 ,
,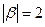 所以
所以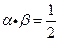 ,由
,由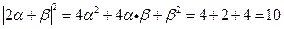
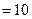 ,所以
,所以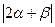 的值为
的值为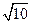 .
.
(14)在如下数表中,已知每行、每列中的数都成等差数列,

那么位于表中的第n行第n+1列的数是 .
14.答案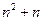
【命题意图】本题主要考查等差数列的有关知识.
【解析】由题,第一列是首项为1,公差为1的等差数列,所以第n行的第一个数为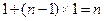 ,由表可得数列的第n行的公差为n,所以第n行的第n+1个数为
,由表可得数列的第n行的公差为n,所以第n行的第n+1个数为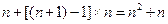 .
.
(15)若正实数x ,y满足2x+y+6=xy,则xy的最小值是 .15.答案18
,y满足2x+y+6=xy,则xy的最小值是 .15.答案18
【命题意图】本题主要考查利用基本不等式求解范围问题.
【解析】由题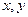 均为正数,
均为正数,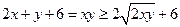 ,令
,令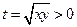 ,则有
,则有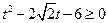 ,解得
,解得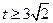 ,即
,即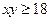 ,所以
,所以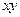 的最小值为18.
的最小值为18.
(16)某商家一月份至五月份累计销售额达3860万元,预测六月份销售额为500万元,七月份销售额比六份递增x%,八月份销售额比七月份递增x%,九、十月份销售总额与七、八月份销售总额相等.若一月至十月份销售总额至少达7000万元,则x的最小值是 .
16.答案20
【命题意图】本题考查二次不等式的实际应用问题,考查学生利用所学知识分析问题解决问题的能力.
【解析】由题知7月份的销售额为500(1+x%),8月份的销售额为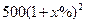 ,所以9月10月份的销售总额为500(1+x%)+
,所以9月10月份的销售总额为500(1+x%)+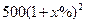 .所以由题可得
.所以由题可得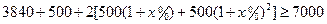 ,令
,令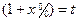 整理可得
整理可得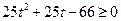 ,解得t的最小值为
,解得t的最小值为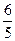 ,所以x的最小值为
,所以x的最小值为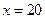 .
.
(17)在平行四边形ABCD中,O是AC与BD的交点,P,Q,M,N分别是线段OA、OB、OC、OD的中点.在A,P,M,C中任取一点记为E,在B,Q,N,D中任取一点记为F.设G为满足向量 的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 .
的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 .
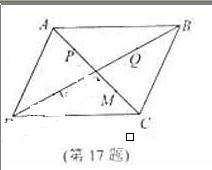
17.答案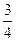
【命题意图】本题主要考查古典概率的有关知识.
【解析】由题可知E总共存在四种可能的位置,F有四种可能的位置,以O为起点,所有的终点 组成的
组成的 基本事件总数为
基本事件总数为
(AD),(AN),(AQ),(AB),(PD),(PN),(PQ),(PB),(MD),(MN),(MQ),(MB),(CD),(CN),(CQ),(CB)共16种,而由平行四边形法则可知满足条件的事件有(AD),(AN), (AQ),(AB) (PB),(PD),(MD),(MB),(CD),(CN),(CQ),(CB)共12种,因此对应的点G构成的集合中点落在平行四边形ABCD的外部的概率为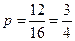 .
.
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤
(18)(本题满分14分)在△ABC中,角A,B,C所对的边分别为a,b,c,设S为△ABC的面积,满足S=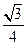 (a2+b2-c2).
(a2+b2-c2).
(Ⅰ)求角C的大小;
(Ⅱ)求sinA+sinB的最大值.
【命题意图】本题主要考查余弦定理、三角形面积公式、三角变换等基础知识同时考查三角运算求解能力.
【答案】(Ⅰ)解:由题意可知
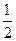 absinC=
absinC=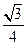 ,2abcosC.
,2abcosC.
所以tanC=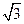 .
.
因为0<C<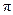 ,
,
所以C=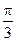 .
.
(Ⅱ)解:由已知sinA+sinB=sinA+sin(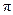 -C-A)=sinA+sin(
-C-A)=sinA+sin(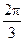 -A)
-A)
=sinA+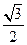 cosA+
cosA+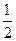 sinA=
sinA=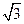 sin(A+
sin(A+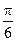 )≤
)≤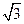 .
.
当△ABC为正三角形时取等号,
所以sinA+sinB的最大值是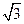 .
.
【点评】在解三角形时,常常将正弦定理、余弦定理结合在一起用,要注意恰当的选取定理,简化运算过程,提高解题速度,痛恨死要注意与平面几何中的有关性质,定理结合起来挖掘题目中的隐含条件.
(19 )(本题满分14分)设a1,d为实数,首项为a1,公差为d的等差数{an}的前n项和为Sn,满足S5S6+
)(本题满分14分)设a1,d为实数,首项为a1,公差为d的等差数{an}的前n项和为Sn,满足S5S6+ 15=0.
15=0.
(Ⅰ)若S5=S.求S6及a1;
(Ⅱ)求d的取值范围.
【命题意图】本题主要考查等差数列的概念、求和公式等基础知识,同时考查运算求解能力及分析问题解决问题的能力.
【答案】
(Ⅰ)解:由题意知S6=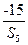 =-3,
=-3,
A6=S6-S5=-8
所以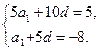
解得a1=7
所以S6= -3,a1=7
(Ⅱ)解:因为S5S6+15=0,
所以(5a1+10d)(6a1+15d)+15=0,
即2a12+9da1+10d2+1=0.
故(4a1+9d)2=d2-8.
所以d2≥8.
故d的取值范围为d≤-2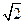 或d≥2
或d≥2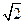 .
.
【点评】等差数列中,通项公式与前n项和公式联系着五个基本量,这五个基本量中,知道其中的三个可以求得另外的两个,往往要解方程或方程组,除掌握这个基本运算关系,还要注意运算中利用等差数列的性质进行整体代换,这样可以简化运算过程.
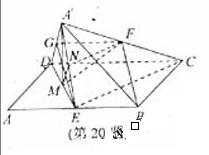
(20)(本题满分14分)如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°,E为线段AB的中线,将△ADE沿直线DE翻折成△A′DE,使平面A′DE⊥平面BCD,F为线段A′C的中点.
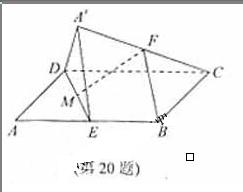
(Ⅰ)求证:BF∥平面A′DE;
(Ⅱ)设M为线段DE的中点,求直线FM与平面
A′DE所成角的余弦值.
【命题意图】本题主要考查空间线线、线面、面面位置关系,线面角等基础知识,同时考查空间想象能力和推理论证能力.
【答案】
(Ⅰ)证明:取A′D的中点G,连结GF,CE,由条件易知
FG∥CD,FG=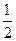 CD.
CD.
BE∥CD,BE=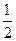 CD.
CD.
所以FG∥BE,FG=BE.
故四边形BEGF为平行四边形,
所以BF∥EG
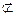 因为
因为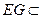 平面A′DE,BF
平面A′DE,BF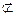 平面A′DE.
平面A′DE.
所以BF//平面A′DE.
(Ⅱ)解:在平行四边形ABCD中,设BC =a,
=a,
则AB=CD=2a,AD=AE=EB=a,
连CE.
因为∠ABC=120°,
在△BCE中,可得CE=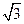 a,
a,
在△ADE中,可得DE=a,
在△CDE中,因为CD2=CE2+DE2,所以CE⊥DE,
在正三角形A′DE中,M为DE中点,所以A′M⊥DE.
由平面A′DE⊥平面BCD,
可知A′M⊥平面BCD,A′M⊥CE.
取A′E的中点N,连线NM、NF,
所以NF⊥DE,NF⊥A′M.
因为DE交A′M于M,
所 以NF⊥平面A′DE,
以NF⊥平面A′DE,
则∠FMN为直线FM与平面A′DE新成角.
在Rt△FMN中,NF=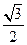 a, MN=
a, MN=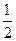 a, FM=a,
a, FM=a,
则cos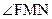 =
=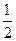 .
.
所以直线FM与平面A′DE所成角的余弦值为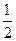 .
.
【点评】空间角的计算方法都是转化为平面角来计算的,直线与平面所成的角是平面的一条斜线和它在平面上的射影所成的锐角(直线与平面垂直或平行包括直线在平面内事,成直角或0°角,我们往往在斜线上取一点向平面引垂线,以形成由平面的斜线、垂线及斜线在平面上的射影组成的直角三角形,这里的关键是引平面的垂线.
(21)(本题满分15分)已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).
(Ⅰ)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.
证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
【命题意图】本题主要考查函数的极值的概念、导数的运算法则、切线方程、导数应用、等差数列等基础知识,同时考查抽象概括、推理论证能力和创新意识.
【答案】
(Ⅰ)解:当a=1,b=2时,
因为f′(x)=(x-1)(3x-5).
故f′(2)=1.
又f(2)=0,
所以f(x)在点(2,0)处的切线方程为y=x-2.
(Ⅱ)证明:因为f′(x)=3(x-a)(x-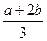 ),
),
由于a<b.
故a<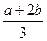 .
.
所以f(x)的两个极值点为x=a,x=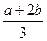 .
.
不妨设x1=a,x2=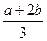 ,
,
因为x3≠x1,x3≠x2,且x3是f(x)的零点,
故x3=b.
又因为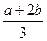 -a=2(b-
-a=2(b-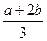 ),
),
x4=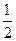 (a+
(a+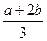 )=
)=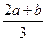 ,
,
所以a,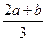 ,
,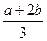 ,b依次成等差数列,
,b依次成等差数列,
所以存在实数x4满足题意,且x4=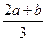 .
.
【点评】本题是一道创新性很强的一道问题,解决此类问题需要灵活的运用所学的知识准确的进行条件之间的转换.另外在解决曲线的切线问题时,要注意曲线“在点p处的切线”是以点P为切点,而“过点P的切线”,点P可能是切点,也可能不是切点,点P可能不在已知的曲线上,切线可能不止一条
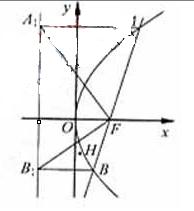
(22)(本题满分15分)已知m是非零实数,抛物线C:y2=2px(p>0)的焦点F在直线l:x-my-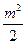 =0上.
=0上.
(Ⅰ)若m=2,求抛物线C的方程;
(Ⅱ)设直线l与抛物线C交于A,B两点,过A,B分别作抛物线C的准线的垂直,垂足为A1,B1,△AA1F,△BB1F的重心分别为G,H.求证:对任意非零实数m,抛物线C的准线与x轴的交点在以线段GH为直径的圆外.
【命题意图】本题主要考查抛物线的几何性质,直线与抛物线、点与圆的位置关系等基础知识,同时考查解析几何的基本思想方法和运算求解能力.
【答案】(Ⅰ)解:因为焦点F(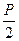 ,0)在直线l上,得
,0)在直线l上,得
p=m2,
又m=2,故p=4.
所以抛物线C的方程为y2=8x.
(Ⅱ)证明:因为抛物线C的焦点F在直线l上,
所以p=m2,
所以抛物线C的方程为y2=2m2x.
设A(x1,y1),B(x2,y2),
由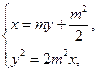 消去x得
消去x得
y2-2m3y-m4=0,
由于m≠0,故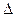 =4m6+4m4>0,
=4m6+4m4>0,
且有y1+y2=2m3,y1y2=-m4,
设M1,M2分别为线段AA1,BB1的中点,
由于2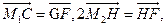
可知G(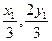 ),H
),H (
(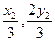 ),
),
所以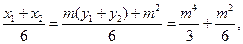
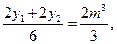
所以GH的中点M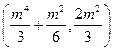 .
.
设R是以线段GH为直径的圆的半径,
则R2=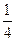
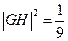 (m2+4)(m2+1)m2.
(m2+4)(m2+1)m2.
设抛物线的准线与x轴交点N(-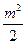 ,0),
,0),
则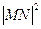 =
=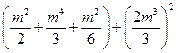
=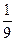 m4(m4+8 m2+4)
m4(m4+8 m2+4)
=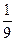 m4[(m2+1)( m2+4)+3m2]
m4[(m2+1)( m2+4)+3m2]
>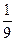 m2 (m2+1)( m2+4)=R2.
m2 (m2+1)( m2+4)=R2.
故N在以线段GH为直径的圆外.
【点评】直线与圆锥曲线相交时解析几何中的一类重要问题,解题时注意应用根与系数的关系及“设而不求”的技巧来解决直线与圆锥曲线的综合性问题.


