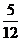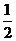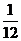(单词翻译:单击)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设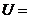
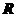 ,
,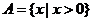 ,
,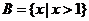 ,则
,则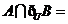 ( )
( )
A.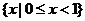 B.
B.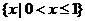 C.
C.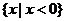 D.
D.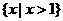
答案:B
【解析】 对于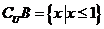 ,因此
,因此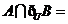
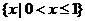 .
.
2.已知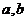 是实数,则“
是实数,则“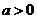 且
且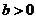 ”是“
”是“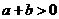 且
且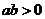 ”的 ( )
”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
答案:C
【解析】对于“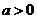 且
且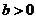 ”可以推出“
”可以推出“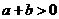 且
且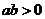 ”,反之也是成立的
”,反之也是成立的
3.设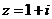 (
(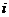 是虚数单位),则
是虚数单位),则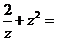 ( )
( )
A.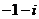 B.
B.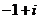 C.
C.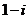 D.
D.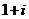
答案:D
【解析】对于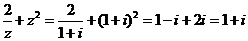
4.在二项式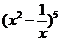 的展开式中,含
的展开式中,含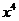 的项的系数是( )
的项的系数是( )

A.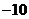 B.
B.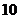
C.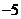 D.
D.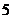
答案:B
【解析】对于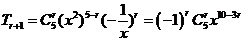 ,对于
,对于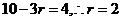 ,则
,则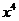 的项的系数是
的项的系数是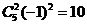
5.在三棱柱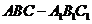 中,各棱长相等,侧掕垂直于底面,点
中,各棱长相等,侧掕垂直于底面,点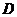 是侧面
是侧面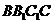 的中心,则
的中心,则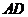 与平面
与平面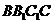 所成角的大小是 ( )
所成角的大小是 ( )
A.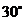 B.
B.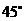 C.
C.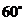 D.
D.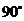
答案:C
【解析】取BC的中点E,则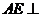 面
面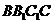 ,
,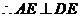 ,因此
,因此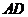 与平面
与平面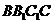 所成角即为
所成角即为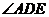 ,设
,设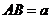 ,则
,则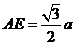 ,
,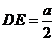 ,即有
,即有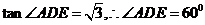 .
.
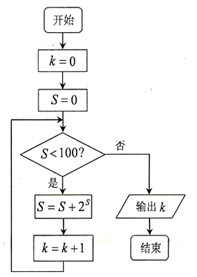
6.某程序框图如图所示,该程序运行后输出的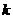 的值是 ( )
的值是 ( )
A.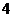 B.
B.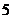 C.
C.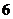 D.
D.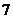
答案:A
【解析】对于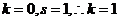 ,而对于
,而对于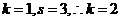 ,则
,则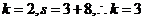 ,后面是
,后面是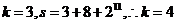 ,不符合条件时输出的
,不符合条件时输出的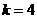 .
.
7.设向量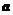 ,
,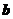 满足:
满足: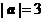 ,
,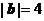 ,
,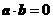 .以
.以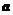 ,
,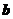 ,
,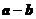 的模为边长构成三角形,则它的边与半径为
的模为边长构成三角形,则它的边与半径为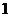 的圆的公共点个数最多为 ( )
的圆的公共点个数最多为 ( )

A.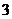 B.
B.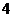 C.
C.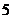 D.
D.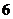
答案:C
【解析】对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有三个交点,对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现.
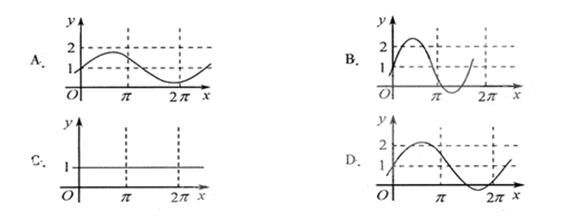
8.已知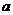 是实数,则函数
是实数,则函数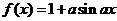 的图象不可能是 ( )
的图象不可能是 ( )
答案:D
【解析】对于振幅大于1时,三角函数的周期为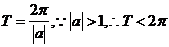 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了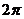 .
.
9.过双曲线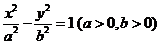 的右顶点
的右顶点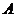 作斜率为
作斜率为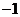 的直线,该直线与双曲线的两条渐近线的交点分别为
的直线,该直线与双曲线的两条渐近线的交点分别为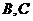 .若
.若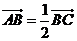 ,则双曲线的离心率是 ( )
,则双曲线的离心率是 ( )

A.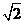 B.
B.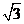 C.
C.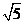 D.
D.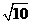
答案:C
【解析】对于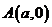 ,则直线方程为
,则直线方程为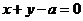 ,直线与两渐近线的交点为B,C,
,直线与两渐近线的交点为B,C,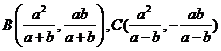 ,则有
,则有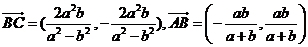 ,因
,因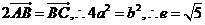 .
.
10.对于正实数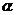 ,记
,记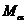 为满足下述条件的函数
为满足下述条件的函数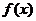 构成的集合:
构成的集合: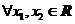 且
且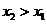 ,有
,有
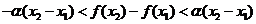 .下列结论中正确的是 ( )
.下列结论中正确的是 ( )
A.若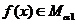 ,
,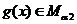 ,则
,则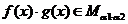
B.若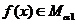 ,
,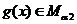 ,且
,且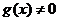 ,则
,则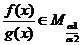
C.若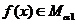 ,
,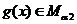 ,则
,则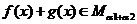


D.若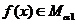 ,
,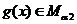 ,且
,且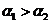 ,则
,则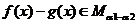
答案:C
【解析】对于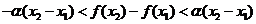 ,即有
,即有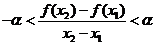 ,令
,令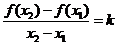 ,有
,有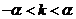 ,不妨设
,不妨设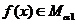 ,
,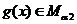 ,即有
,即有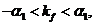
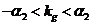 ,因此有
,因此有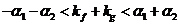 ,因此有
,因此有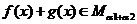 .
.
非选择题部分(共100分)
二、填空题:本大题共7小题,每小题4分,共28分。
11.设等比数列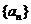 的公比
的公比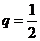 ,前
,前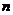 项和为
项和为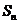 ,则
,则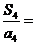 __________.
__________.
答案:15
【解析】对于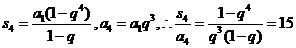
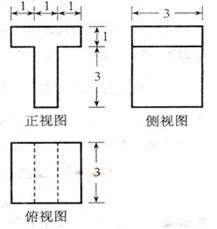
12.若某几何体的三视图(单位: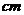 )如图所示,则此几何体的体积是________
)如图所示,则此几何体的体积是________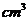 .
.
答案:18
【解析】该几何体是由二个长方体组成,下面体积为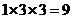 ,上面的长方体体积为
,上面的长方体体积为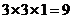 ,因此其几何体的体积为18
,因此其几何体的体积为18
13.若实数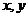 满足不等式组
满足不等式组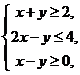 则
则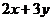 的最小值是_________.
的最小值是_________.

答案:4
【解析】通过画出其线性规划,可知直线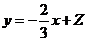 过点
过点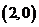 时,
时,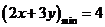
14.某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如
下:
高峰时间段用电价格表 | 低谷时间段用电价格表 | ||
高峰月用电量 (单位:千瓦时) | 高峰电价 (单位:元/千瓦时) | 低谷月用电量 (单位:千瓦时) | 低谷电价 (单位:元/千瓦时) |
50及以下的部分 | 0.568 | 50及以下的部分 | 0.288 |
超过50至200的部分 | 0.598 | 超过50至200的部分 | 0.318 |
超过200的部分 | 0.668 | 超过200的部分 | 0.388 |
若某家庭5月份的高峰时间段用电量为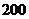 千瓦时,低谷时间段用电量为
千瓦时,低谷时间段用电量为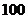 千瓦时,则按这种计费方式该家庭本月应付的电费为 ___________元(用数字作答).
千瓦时,则按这种计费方式该家庭本月应付的电费为 ___________元(用数字作答).

答案: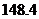
【解析】对于应付的电费应分二部分构成,高峰部分为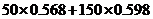 ;对于低峰部分为
;对于低峰部分为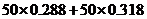 ,二部分之和为
,二部分之和为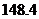
15.观察下列等式:
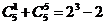 ,
,
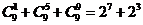 ,
,
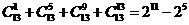 ,
,
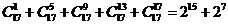 ,
,
………
由以上等式推测到一个一般的结论:
对于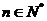 ,
,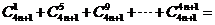 ___________.
___________.

答案: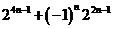
【解析】这是一种需类比推理方法破解的问题,结论由二项构成,第二项前有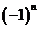 ,二项指数分别为
,二项指数分别为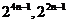 ,因此对于
,因此对于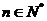 ,
,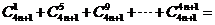
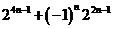
16.甲、乙、丙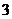 人站到共有
人站到共有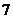 级的台阶上,若每级台阶最多站
级的台阶上,若每级台阶最多站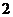 人,同一级台阶上的人不区分站的位置,则不同的站法种数是_____________(用数字作答).
人,同一级台阶上的人不区分站的位置,则不同的站法种数是_____________(用数字作答).
答案:336
【解析】对于7个台阶上每一个只站一人,则有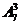 种;若有一个台阶有2人,另一个是1人,则共有
种;若有一个台阶有2人,另一个是1人,则共有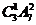 种,因此共有不同的站法种数是336种.
种,因此共有不同的站法种数是336种.

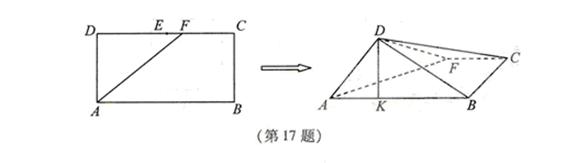
17.如图,在长方形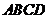 中,
中,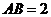 ,
,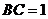 ,
,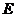 为
为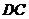 的中点,
的中点,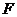 为线段
为线段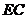 (端点除外)上一动点.现将
(端点除外)上一动点.现将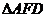 沿
沿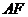 折起,使平面
折起,使平面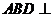 平面
平面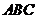 .在平面
.在平面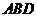 内过点
内过点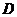
作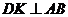 ,
,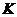 为垂足.设
为垂足.设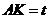 ,则
,则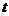 的取值范围是___________.
的取值范围是___________.
答案: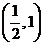
【解析】此题的破解可采用二个极端位置法,即对于F位于DC的中点时,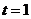 ,随着F点到C点时,因
,随着F点到C点时,因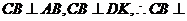 平面
平面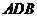 ,即有
,即有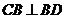 ,对于
,对于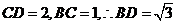 ,又
,又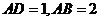 ,因此有
,因此有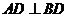 ,则有
,则有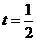 ,因此
,因此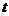 的取值范围是
的取值范围是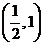


三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.(本题满分14分)在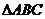 中,角
中,角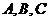 所对的边分别为
所对的边分别为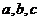 ,且满足
,且满足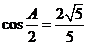 ,
,
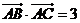 . (I)求
. (I)求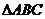 的面积; (II)若
的面积; (II)若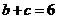 ,求
,求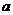 的值.
的值.
解析:(I)因为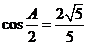 ,
,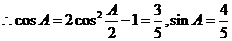 ,又由
,又由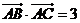 ,得
,得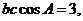
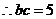 ,
,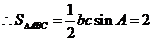


(II)对于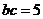 ,又
,又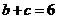 ,
,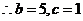 或
或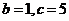 ,由余弦定理得
,由余弦定理得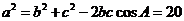 ,
,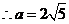


19.(本题满分14分)在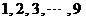 这
这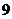 个自然数中,任取
个自然数中,任取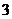 个数.
个数.
(I)求这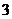 个数中恰有
个数中恰有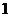 个是偶数的概率;
个是偶数的概率;
(II)设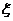 为这
为这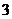 个数中两数相邻的组数(例如:若取出的数为
个数中两数相邻的组数(例如:若取出的数为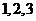 ,则有两组相邻的数
,则有两组相邻的数
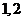 和
和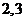 ,此时
,此时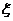 的值是
的值是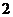 ).求随机变量
).求随机变量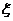 的分布列及其数学期望
的分布列及其数学期望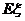 .
.
解析:
(I)记“这3个数恰有一个是偶数”为事件A,则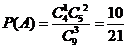 ;
;

(II)随机变量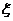 的取值为
的取值为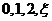 的分布列为
的分布列为
| 0 | 1 | 2 |
P |
|
|
|
所以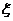 的数学期望为
的数学期望为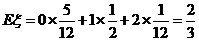


20.(本题满分15分)如图,平面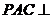 平面
平面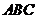 ,
,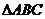 是以
是以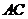 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,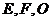 分别为
分别为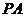 ,
,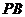 ,
,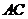 的中点,
的中点,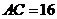 ,
,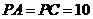 .
.
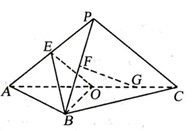
(I)设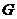 是
是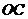 的中点,证明:
的中点,证明: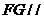 平面
平面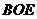 ;
;
(II)证明:在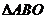 内存在一点
内存在一点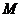 ,使
,使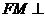 平面
平面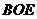 ,并求点
,并求点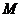 到
到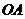 ,
,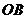 的距离.
的距离.
证明:(I)如图,连结OP,以O为坐标原点,分别以OB、OC、OP所在直线为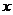 轴,
轴,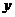 轴,
轴,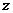 轴,建立空间直角坐标系O
轴,建立空间直角坐标系O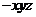 ,
,

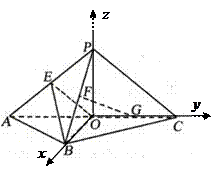
则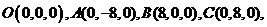
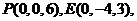
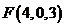 ,由题意得,
,由题意得,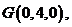 因
因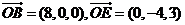 ,因此平面BOE的法向量为
,因此平面BOE的法向量为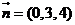 ,
,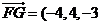 得
得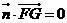 ,又直线
,又直线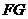 不在平面
不在平面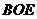 内,因此有
内,因此有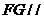 平面
平面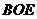
(II)设点M的坐标为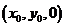 ,则
,则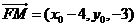 ,因为
,因为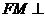 平面BOE,所以有
平面BOE,所以有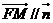 ,因此有
,因此有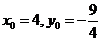 ,即点M的坐标为
,即点M的坐标为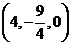 ,在平面直角坐标系
,在平面直角坐标系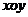 中,
中,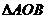 的内部区域满足不等式组
的内部区域满足不等式组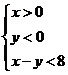 ,经检验,点M的坐标满足上述不等式组,所以在
,经检验,点M的坐标满足上述不等式组,所以在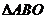 内存在一点
内存在一点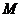 ,使
,使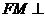 平面
平面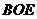 ,由点M的坐标得点
,由点M的坐标得点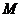 到
到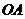 ,
,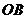 的距离为
的距离为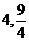 .
.

21.(本题满分15分)已知椭圆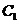 :
: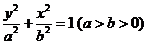 的右顶点为
的右顶点为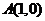 ,过
,过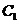 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为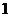 .
.
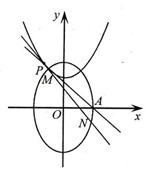
(I)求椭圆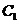 的方程;
的方程;
(II)设点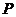 在抛物线
在抛物线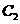 :
: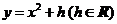 上,
上,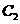 在点
在点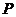 处的切线与
处的切线与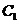 交于点
交于点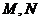 .当线段
.当线段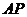 的中点与
的中点与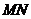 的中点的横坐标相等时,求
的中点的横坐标相等时,求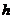 的最小值.
的最小值.
解析:
(I)由题意得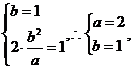 所求的椭圆方程为
所求的椭圆方程为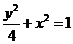 ,
,

(II)不妨设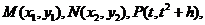 则抛物线
则抛物线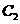 在点P处的切线斜率为
在点P处的切线斜率为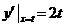 ,直线MN的方程为
,直线MN的方程为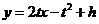 ,将上式代入椭圆
,将上式代入椭圆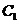 的方程中,得
的方程中,得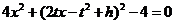 ,即
,即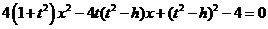 ,因为直线MN与椭圆
,因为直线MN与椭圆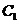 有两个不同的交点,所以有
有两个不同的交点,所以有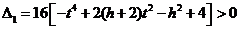 ,
,
设线段MN的中点的横坐标是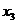 ,则
,则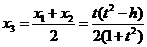 ,
,

设线段PA的中点的横坐标是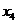 ,则
,则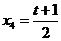 ,由题意得
,由题意得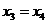 ,即有
,即有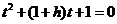 ,其中的
,其中的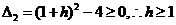 或
或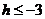 ;
;
当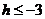 时有
时有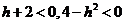 ,因此不等式
,因此不等式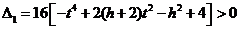 不成立;因此
不成立;因此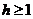 ,当
,当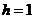 时代入方程
时代入方程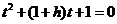 得
得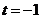 ,将
,将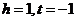 代入不等式
代入不等式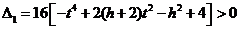 成立,因此
成立,因此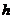 的最小值为1.
的最小值为1.
22.(本题满分14分)已知函数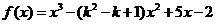 ,
,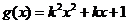 ,
,
其中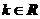 .
.

(I)设函数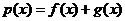 .若
.若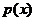 在区间
在区间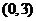 上不单调,求
上不单调,求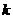 的取值范围;
的取值范围;
(II)设函数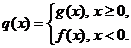 是否存在
是否存在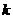 ,对任意给定的非零实数
,对任意给定的非零实数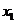 ,存在惟一的非零实数
,存在惟一的非零实数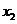 (
(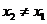 ),使得
),使得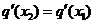 成立?若存在,求
成立?若存在,求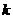 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
解析:(I)因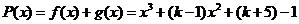 ,
,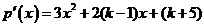 ,因
,因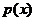 在区间
在区间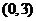 上不单调,所以
上不单调,所以 在
在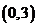 上有实数解,且无重根,由
上有实数解,且无重根,由 得
得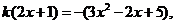


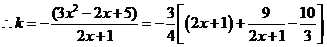 ,令
,令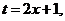 有
有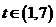 ,记
,记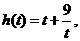 则
则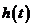 在
在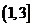 上单调递减,在
上单调递减,在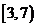 上单调递增,所以有
上单调递增,所以有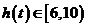 ,于是
,于是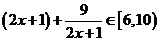 ,得
,得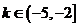 ,而当
,而当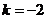 时有
时有 在
在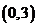 上有两个相等的实根
上有两个相等的实根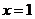 ,故舍去,所以
,故舍去,所以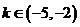 ;
;

(II)当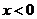 时有
时有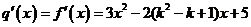 ;
;
当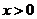 时有
时有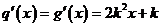 ,因为当
,因为当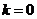 时不合题意,因此
时不合题意,因此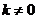 ,
,
下面讨论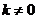 的情形,记A
的情形,记A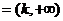 ,B=
,B=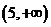 (ⅰ)当
(ⅰ)当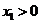 时,
时,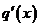 在
在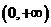 上单调递增,所以要使
上单调递增,所以要使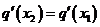 成立,只能
成立,只能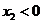 且
且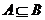 ,因此有
,因此有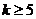 ,(ⅱ)当
,(ⅱ)当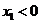 时,
时,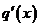 在
在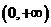 上单调递减,所以要使
上单调递减,所以要使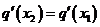 成立,只能
成立,只能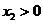 且
且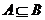 ,因此
,因此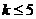 ,综合(ⅰ)(ⅱ)
,综合(ⅰ)(ⅱ)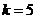 ;
;
当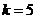 时A=B,则
时A=B,则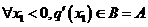 ,即
,即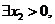 使得
使得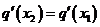 成立,因为
成立,因为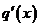 在
在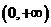 上单调递增,所以
上单调递增,所以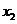 的值是唯一的;
的值是唯一的;
同理,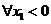 ,即存在唯一的非零实数
,即存在唯一的非零实数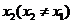 ,要使
,要使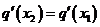 成立,所以
成立,所以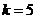 满足题意.
满足题意.