(单词翻译:单击)
第Ⅰ卷(共60分)
一、选择题:本大题共l0小题.每小题5分,共50分在每小题给出的四个选项中,只有一项是满足题目要求的.

【解析】因为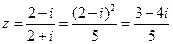 ,故复数z对应点在第四象限,选D.
,故复数z对应点在第四象限,选D.
3.若点(a,9)在函数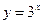 的图象上,则tan=
的图象上,则tan=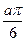 的值为
的值为
(A)0 (B) 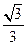 (C) 1 (D)
(C) 1 (D) 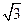
【答案】D
【解析】由题意知:9=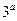 ,解得
,解得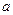 =2,所以
=2,所以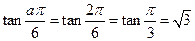 ,故选D.
,故选D.

5. 对于函数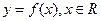 ,“
,“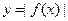 的图象关于y轴对称”是“
的图象关于y轴对称”是“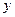 =
=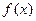 是奇函数”的
是奇函数”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充要条件 (D)既不充分也不必要
【答案】B
【解析】由奇函数定义,容易得选项B正确.
6.若函数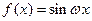 (ω>0)在区间
(ω>0)在区间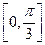 上单调递增,在区间
上单调递增,在区间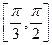 上单调递减,则ω=
上单调递减,则ω=
(A)3 (B)2 (C)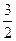 (D)
(D)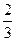
【答案】C
【解析】由题意知,函数在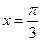 处取得最大值1,所以1=sin
处取得最大值1,所以1=sin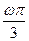 ,故选C.
,故选C.
7. 某产品的广告费用x与销售额y的统计数据如下表

根据上表可得回归方程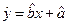 中的
中的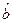 为9.4,据此模型预报广告费用为6万元时销售额为
为9.4,据此模型预报广告费用为6万元时销售额为
(A)63.6万元 (B)65.5万元 (C)67.7万元 (D)72.0万元
【答案】B
【解析】由表可计算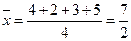 ,
,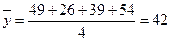 ,因为点
,因为点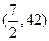 在回归直线
在回归直线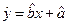 上,且
上,且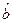 为9.4,所以
为9.4,所以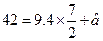 , 解得
, 解得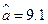 ,故回归方程为
,故回归方程为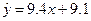 , 令x=6得
, 令x=6得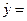 65.5,选B.
65.5,选B.
8.已知双曲线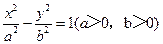 的两条渐近线均和圆C:
的两条渐近线均和圆C: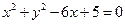 相切,且双曲线的右焦点为圆C的圆心,则该双曲
相切,且双曲线的右焦点为圆C的圆心,则该双曲 线的方程为
线的方程为
(A)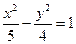 (B)
(B) 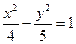 (C)
(C) 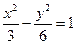 (D)
(D) 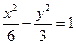
【答案】A
【解析】由圆C: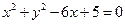 得:
得: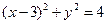 ,因为双曲线的右焦点为圆C的圆心(3,0),所以c=3,又双曲线的两条渐近线
,因为双曲线的右焦点为圆C的圆心(3,0),所以c=3,又双曲线的两条渐近线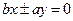 均和圆C相切,所以
均和圆C相切,所以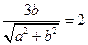 ,即
,即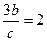 ,又因为c=3,所以b=2,即
,又因为c=3,所以b=2,即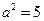 ,所以该双曲线的方程为
,所以该双曲线的方程为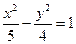 ,故选A.
,故选A.
9. 函数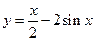 的图象大致是
的图象大致是
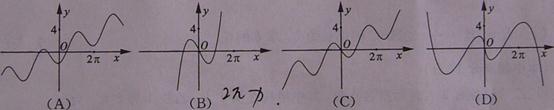
【答案】C
【解析】因为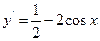 ,所以令
,所以令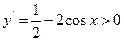 ,得
,得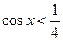 ,此时原函数是增函数;令
,此时原函数是增函数;令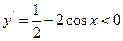 ,得
,得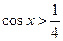 ,此时原函数是减函数,结合余弦函数图象,可得选C正确.
,此时原函数是减函数,结合余弦函数图象,可得选C正确.
10. 已知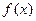 是
是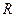 上最小正周期为2的周期函数,且当
上最小正周期为2的周期函数,且当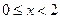 时,
时,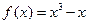 ,则函数
,则函数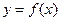 的图象在区间[0,6]上与
的图象在区间[0,6]上与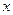 轴的交点的个数为
轴的交点的个数为
(A)6 (B)7 (C)8 (D)9
【答案】A
【解析】因为当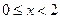 时,
时, 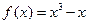 ,又因
,又因 为
为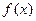 是
是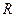 上最小正周期为2的周期函数,且
上最小正周期为2的周期函数,且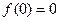 ,所以
,所以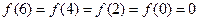 ,又因为
,又因为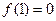 ,所以
,所以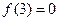 ,
,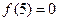 ,故函数
,故函数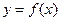 的图象在区间[0,6]上与
的图象在区间[0,6]上与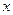 轴的交点的个数为6个,选A.
轴的交点的个数为6个,选A.
11.下图是长和宽分别相等的两个矩形.给定下列三个命题:①存在三棱 柱,其正(主)视图、俯视图如下图;②存在四棱柱,其正(主)视图、俯视图如下图;③存在圆柱,其正(主)视图、俯视图如下图.其中真命题的个数是
柱,其正(主)视图、俯视图如下图;②存在四棱柱,其正(主)视图、俯视图如下图;③存在圆柱,其正(主)视图、俯视图如下图.其中真命题的个数是
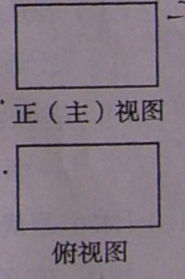
(A)3 (B)2 (C)1 (D)0
【答案】A
【解析】对于①,可以是放倒的三棱柱;容易判断②③可以.
12.设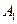 ,
,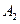 ,
,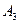 ,
,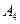 是平面直角坐标系中两两不同的四点,若
是平面直角坐标系中两两不同的四点,若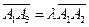 (λ∈R),
(λ∈R),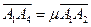 (μ∈R),且
(μ∈R),且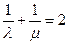 ,则称
,则称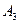 ,
,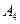 调和分割
调和分割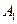 ,
,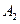 ,已知点C(c,o),D(d,O
,已知点C(c,o),D(d,O )
) (c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是
(c,d∈R)调和分割点A(0,0),B(1,0),则下面说法正确的是
(A)C可能是线段AB的中点
(B)D可能是线段AB的中点
(C)C,D可能同时在线段AB上
(D) C,D不可 能同时在线段AB的延长线上
能同时在线段AB的延长线上
【答案】D
【解析】由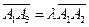 (λ∈R),
(λ∈R),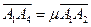 (μ∈R)知:四点
(μ∈R)知:四点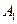 ,
,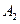 ,
,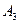 ,
,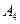 在同一条直线上,
在同一条直线上,
因为C,D调和分割点A,B,所以A,B,C,D四点在同一直线上,且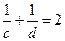 , 故选D.
, 故选D.
二、填空题:本大题共4小题,每小题4分,共16分.
13.执行右图所示的程序框图,输入l=2,m=3,n=5,则输出的y的值是 .
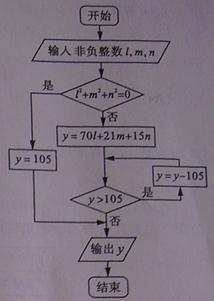
【答案】68
【解析】由输入l=2,m=3,n=5,计算得出y=278,第一次得新的y=173;第二次得新的y=68<105,输出y.
14. 若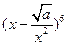 展开式的常数项为60,则常数
展开式的常数项为60,则常数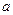 的值为 .
的值为 .
【答案】4
【解析】因为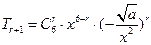 ,所以r=2, 常数项为
,所以r=2, 常数项为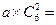 60,解得
60,解得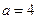 .
.
15. 设函数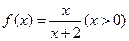 ,观察:
,观察:
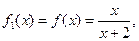
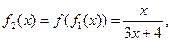
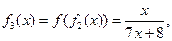
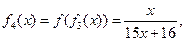
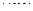
根据以上事实,由归纳推理可得:
当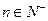 且
且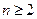 时,
时,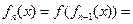 .
.
【答案】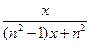
【解析】观察知:四个等式等号右边的分母为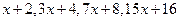 ,即
,即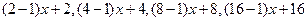 ,所以归纳出分母为
,所以归纳出分母为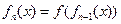 的分母为
的分母为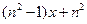 ,故当
,故当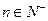 且
且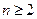 时,
时,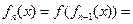
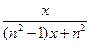 .
.
16.已知函数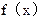 =
=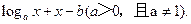 当2<a<3<b<4时,函数
当2<a<3<b<4时,函数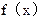
 的零点
的零点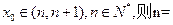 .
.
【答案】5
【解析】方程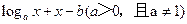 =0的根为
=0的根为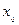 ,即函数
,即函数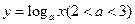 的图象与函数
的图象与函数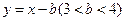 的交点横坐标为
的交点横坐标为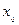 ,且
,且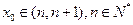 ,结合图象,因为当
,结合图象,因为当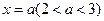 时,
时,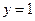 ,此时对应直线上
,此时对应直线上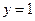 的点的横坐标
的点的横坐标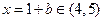 ;当
;当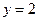 时, 对数函数
时, 对数函数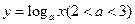 的图象上点的横坐标
的图象上点的横坐标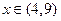 ,直线
,直线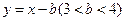 的图象上点的横坐标
的图象上点的横坐标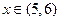 ,故所求的
,故所求的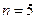 .
.
三、解答题:本大题共6小题,共74分.
17.(本小题满分12分)
在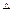 ABC中
ABC中 ,内角A,B,C的对边分别为a,b,c.已知
,内角A,B,C的对边分别为a,b,c.已知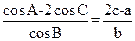 .
.
(I)求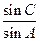 的值;
的值;
(II)若cosB=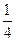 ,
,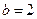 ,求
,求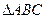 的面积.
的面积.
【解析】(Ⅰ)由正弦定理得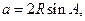
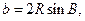
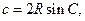 所以
所以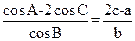 =
=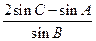 ,即
,即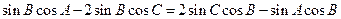 ,即有
,即有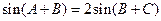 ,即
,即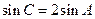 ,所以
,所以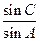 =2.
=2.
(Ⅱ)由(Ⅰ)知: 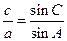 =2,即c=2a,又因为
=2,即c=2a,又因为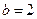 ,所以由余弦定理得:
,所以由余弦定理得:
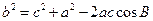 ,即
,即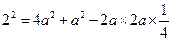 ,解得
,解得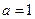 ,所以c=2,又因为cosB=
,所以c=2,又因为cosB=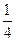 ,所以sinB=
,所以sinB=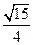 ,故
,故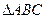 的面积为
的面积为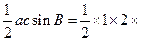
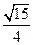 =
=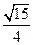 .
.
18.(本小题满分12分)
红队队员甲、乙、丙与蓝队队员A、B、C进行围棋比赛,甲对A,乙对B,丙对C各一盘,已知甲胜A,乙胜B,丙胜C的概率分别为0.6,0.5,0.5,假设各盘比赛结果相互独立。
(Ⅰ)求红队至少两名队员获胜的概率;
(Ⅱ)用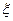 表示红队队员获胜的总盘数,求
表示红队队员获胜的总盘数,求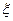 的分布列和数学期望
的分布列和数学期望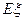 .
.
【解析】(Ⅰ)红队至少两名队员获胜的概率为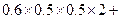
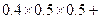
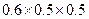 =0.55.
=0.55.
(Ⅱ)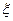 取的可能结果为0,1,2,3,则
取的可能结果为0,1,2,3,则
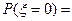
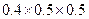 =0.1;
=0.1;
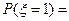
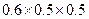 +
+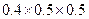 +
+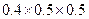 =0.35;
=0.35;
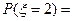
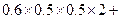
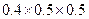 =0.4;
=0.4;
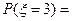
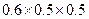 =0.15.
=0.15.
所以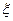 的分布列为
的分布列为
| 0 | 1 | 2 | 3 |
P | 0.1 | 0.35 | 0.4 | 0.15 |
数学期望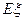 =0×0.1+1×0.35+2×0.4+3×0.
=0×0.1+1×0.35+2×0.4+3×0. 15=1.6.
15=1.6.
19.(本小题满分12分)
在如图所示的几何体中,四边形ABCD为平行四边形,∠ ACB=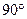 ,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC.AB=2EF.
,EA⊥平面ABCD,EF∥AB,FG∥BC,EG∥AC.AB=2EF.
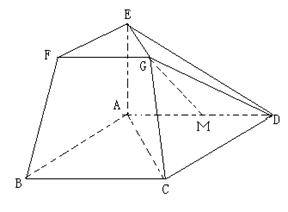
(Ⅰ)若M是线段AD的中点,求证:GM∥平面ABFE;
(Ⅱ)若AC=BC=2AE,求二面角A-BF-C的大小.
【解析】(Ⅰ)连结AF,因为EF∥AB,FG∥BC,
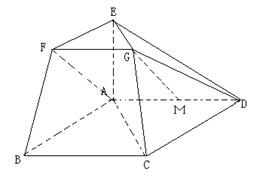
EF∩FG=F,所以平面EFG∥平面ABCD,又易证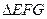 ∽
∽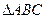 ,
,
所以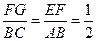 ,即
,即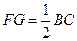 ,即
,即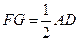 ,又M为AD
,又M为AD
的中点,所以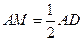 ,
, 又因为FG∥BC∥AD,所以FG∥AM,所以四边形AMGF是平行四边形,故GM∥FA,又因为GM
又因为FG∥BC∥AD,所以FG∥AM,所以四边形AMGF是平行四边形,故GM∥FA,又因为GM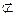 平面ABFE,FA
平面ABFE,FA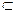 平面ABFE,所以GM∥平面ABFE.
平面ABFE,所以GM∥平面ABFE.
(Ⅱ)取AB的中点O,连结CO,因为AC=BC,所以CO⊥AB,
又因为EA⊥平面AB CD,CO
CD,CO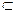 平面ABCD,所以EA⊥CO,
平面ABCD,所以EA⊥CO,
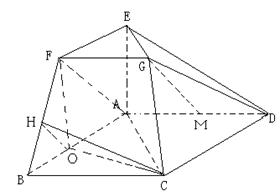
又EA∩AB=A,所以CO⊥平面ABFE,在平面ABEF内,过点O作OH⊥BF于H,连结CH,由三垂线定理知: CH⊥BF,所以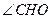 为二
为二 面角A-BF-C的平面角.
面角A-BF-C的平面角.
设AB=2EF=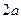 ,因为∠ ACB=
,因为∠ ACB=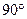 ,AC=BC=
,AC=BC=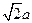 ,CO=
,CO=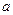 ,
,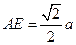 ,连结FO,容易证得FO∥EA且
,连结FO,容易证得FO∥EA且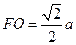 ,所以
,所以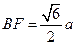 ,所以OH=
,所以OH=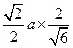 =
=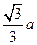 ,所以在
,所以在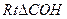 中,tan∠ CHO=
中,tan∠ CHO=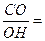
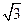 ,故∠ CHO=
,故∠ CHO=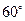 ,所以二面角A-BF-C的大小为
,所以二面角A-BF-C的大小为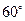 .
.
20.(本小题满分12分)
等比数列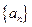 中,
中,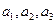 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且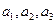 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
第一列 | 第二列 | 第三列 | |
第一行 | 3 | 2 | 10 |
第二行 | 6 | 4 | 14 |
第三行 | 9 | 8 | 18 |
(Ⅰ) 求数列
求数列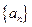 的通项公式;
的通项公式;
(Ⅱ)若数列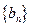 满足:
满足: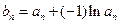 ,求数列
,求数列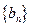 的前
的前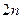 项和
项和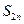 .
.
【解析】(Ⅰ)由题意知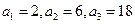 ,因为
,因为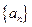 是等比数列,所以公比为3,所以数列
是等比数列,所以公比为3,所以数列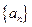 的通项公式
的通项公式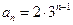 .
.
(Ⅱ)因为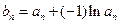 =
=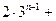
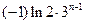 , 所以
, 所以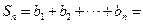
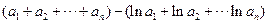 =
=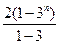 -
-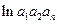 =
=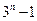 -
-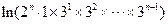 =
=
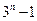 -
-
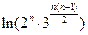 ,所以
,所以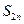 =
=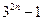 -
-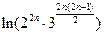 =
=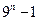 -
-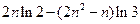 .
.
21.(本小题满分 12分)
12分)
某 企
企 业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为
业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端均为半球形,按照设计要求容器的体积为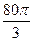 立方米,且
立方米,且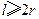 .假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为
.假设该容器的建造费用仅与其表面积有关.已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米建造费用为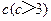 .设该容器的建造费用为
.设该容器的建造费用为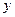 千元.
千元.

(Ⅰ)写出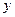 关于
关于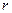 的函数表达式,并求该函
的函数表达式,并求该函 数的定义域;
数的定义域;
(Ⅱ)求该容器的建造费用最小时的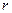 .
.
【解析】(Ⅰ)因为容器的体积为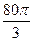 立方米,所以
立方米,所以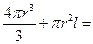
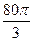 ,解得
,解得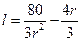 ,所以圆柱的侧面积为
,所以圆柱的侧面积为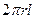 =
=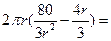
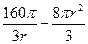 ,两端两个半球的表面积之和为
,两端两个半球的表面积之和为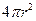 ,所以
,所以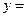
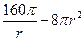 +
+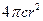 ,定义域为(0,
,定义域为(0,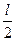 ).
).
(Ⅱ)因为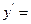
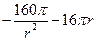 +
+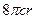 =
=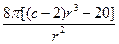 ,所以令
,所以令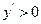 得:
得: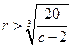 ; 令
; 令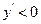 得:
得: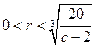 ,所以
,所以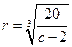 米时, 该容器的建造费用最小.
米时, 该容器的建造费用最小.
22.(本小题满分14分)
已知动直线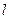 与椭圆C:
与椭圆C: 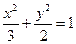 交于P
交于P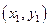 、Q
、Q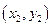 两不同点,且△OPQ的面积
两不同点,且△OPQ的面积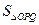 =
=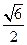 ,其中O为坐标原点.
,其中O为坐标原点.
(Ⅰ)证明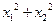 和
和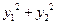 均为定值;
均为定值;
(Ⅱ)设线段PQ的中点为M,求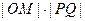 的最大值;
的最大值;
(Ⅲ)椭圆C上是否存在点D,E,G,使得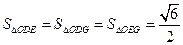 ?若存在,判断△DEG的形状;若不存在,请说明理由.
?若存在,判断△DEG的形状;若不存在,请说明理由.
【解析】(参考标准答案)


