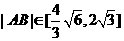(单词翻译:单击)
一、选择题:本大题共12小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合题目要求的。
(1)集合A={0,2,a},B={1,a2}.若A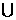 B={0,1,2,4,16},则a的值为
B={0,1,2,4,16},则a的值为
(A)0 (B)1 (C)2 (D)4
(2)复数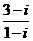 等于
等于
(A)1+2i (B)1-2i (C)2 +i (D)2 – i
(3) 将函数y=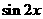 的图像向左平移
的图像向左平移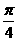 个单位,再向上平移1个单位,所得图像的函数解析式是
个单位,再向上平移1个单位,所得图像的函数解析式是
(A)y=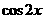 (B)y=
(B)y=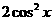
(C)y=1+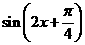 (D)y=
(D)y=
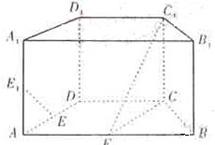
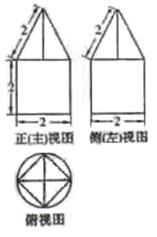
(4)一空间几何体的三视图如图所示,则该几何体的体积为
(A)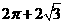 (B)
(B)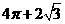
(C)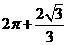 (D)
(D)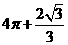
(5)已知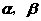 表示两个不同的平面,m为平面
表示两个不同的平面,m为平面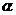 内的一条直线,则“
内的一条直线,则“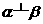 ”是“
”是“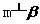 ”的
”的
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
(6)函数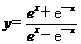 的图象大致为
的图象大致为
(7)设p是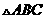 所在平面内的一点,
所在平面内的一点,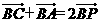 ,则
,则
(A)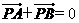
 (B)
(B)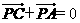
(C)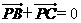 (D)
(D)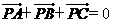
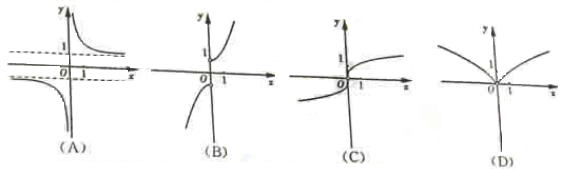
(8)某工厂对一批产品进行了抽样检测。右图是根据抽样检测后的产品净重(单位:克)数据绘制的频率分布直方图,其中产品净重的范围是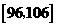 ,样本数据分组为
,样本数据分组为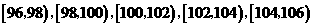
已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是
(A)90 (B)75
(C)60 (D)45
(9)设双曲线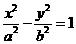 的一条渐近线与抛物线
的一条渐近线与抛物线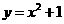 只有一个公共点,则双曲线的离心率为
只有一个公共点,则双曲线的离心率为
(A)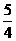 (B)
(B) 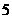 (C)
(C) 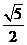 (D)
(D) 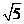
(10) 定义在R上的函数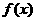 满足
满足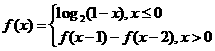 ,则
,则 的值为
的值为
(A)-1 (B) 0 (C) 1 (D) 2
(11)在区间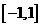 上随机取一个数
上随机取一个数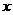 ,
,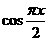 的值介于0到
的值介于0到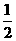 之间的概率为
之间的概率为
(A)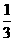 (B)
(B) 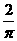 (C)
(C) 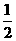 (D)
(D) 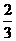
(12)设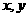 满足约束条件
满足约束条件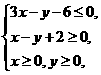 若目标函数
若目标函数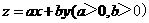 的最大值为12,则
的最大值为12,则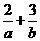 的最小值为
的最小值为
(A)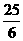 (B)
(B) 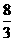 (C)
(C) 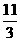 (D) 4
(D) 4
二、填空题:本大题共4小题,每小题4分,共16分. (注意:在试题卷上作答无效)
(13)不等式 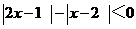 的解集为__________.
的解集为__________.
(14)若函数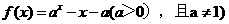 有两个零点,则实数
有两个零点,则实数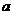 的取值范围是_________.
的取值范围是_________.
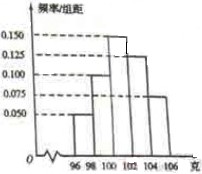
(15)执行右边的程序框图,输出的T=_________.
(16)已知定义在R上的奇函数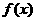 满足
满足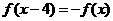 ,且在区间[0,2]上是增函数.若方程
,且在区间[0,2]上是增函数.若方程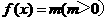 在区间[-8,8]上有四个不同的根
在区间[-8,8]上有四个不同的根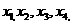 则
则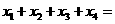 _________.
_________.
三、解答题:本大题共6小题,共74分。
(17)(本小题满分12分)(注意:在试题卷上作答无效)
设函数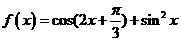 。
。
(Ⅰ)求函数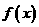 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅱ)设A,B,C为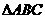 的三个内角,若
的三个内角,若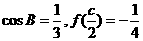 ,且C为锐角,求
,且C为锐角,求
 。
。
(18)(本小题满分12分)(注意:在试题卷上作答无效)
如图,在直四棱柱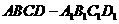 中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,
中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,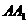 ,AB的中点。
,AB的中点。
(Ⅰ)证明:直线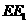 ∥平面
∥平面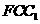 ;
;
(Ⅱ)求二面角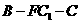 的弦值。
的弦值。
(19)(本小题满分12分) (注意:在试题卷上作答无效)
在某学校组织的一次蓝球定点投蓝训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分;如果前两次得分之和超过3分即停止投篮,否则投三次。某同学在A处的命中率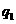 为0.25,在B处的命中率为
为0.25,在B处的命中率为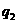 .该同学选择先在A处投一球,以后都在B处投,用
.该同学选择先在A处投一球,以后都在B处投,用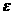 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为

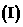 求
求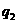 的值;
的值;
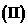 求随机变量
求随机变量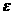 的数学期量
的数学期量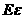 ;
;
 试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
试比较该同学选择都在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小。
20.(本小题满分12分)(注意:在试题卷上作答无效)
等比数列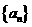 的前n项和为,已知对任意的
的前n项和为,已知对任意的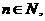 ,点
,点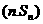 均在函数
均在函数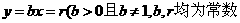 的图象上。
的图象上。
(Ⅰ)求r的值。
(Ⅱ)当b=2时,记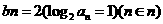 证明:对任意的,不等式成立
证明:对任意的,不等式成立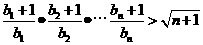
(21)(本小题满分12分)(注意:在试题卷上作答无效)
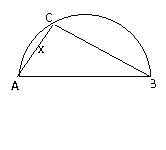
两县城A和B相距20Km,现计划在两县城外以AB为直径的半圆弧
 上选择一点C建造垃圾理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与对城B的影响度之和。记C点到城A的距离xKm,建在C处的垃圾处理厂对城B的影响度为Y,统计调查表明;垃圾处理厂对城A的影响度与所选地点到城B的平方成反比,比例系数为4;城B的影响度与所选地点到城B的距离的平方成反比,比例系数为K,当垃圾处理厂建在弧
上选择一点C建造垃圾理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与对城B的影响度之和。记C点到城A的距离xKm,建在C处的垃圾处理厂对城B的影响度为Y,统计调查表明;垃圾处理厂对城A的影响度与所选地点到城B的平方成反比,比例系数为4;城B的影响度与所选地点到城B的距离的平方成反比,比例系数为K,当垃圾处理厂建在弧 的中点时,对城A和城B)总影响度为0.065
的中点时,对城A和城B)总影响度为0.065
(Ⅰ)将Y表示成X的函数;
(Ⅱ)讨论(Ⅰ)中函数的单调性,并判断弧 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点城A的距离;若不存在,说明理由。
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点城A的距离;若不存在,说明理由。
(22)(本小题满分14分)(注意:在试题卷上作答无效)
设椭圆E: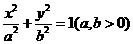
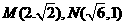 ,O为坐标原点
,O为坐标原点
(Ⅰ)求椭圆E的方程;
(Ⅱ)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒在两个交点A,B且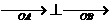 ?若存在,写出该圆的方程,关求
?若存在,写出该圆的方程,关求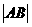 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
2009年普通高等学校招生全国统一考试(山东卷)
理科数学(参考答案)
一、选择题
1-12 D C B C B A B A D C A A
1. 【解析】:∵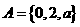 ,
,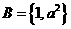 ,
,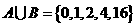 ∴
∴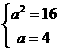 ∴
∴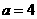 ,故选D.
,故选D.
答案:D
2. 【解析】: 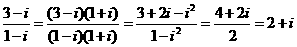 ,故选C.答案:C
,故选C.答案:C
3. 【解析】:将函数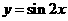 的图象向左平移
的图象向左平移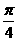 个单位,得到函数
个单位,得到函数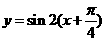 即
即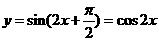 的图象,再向上平移1个单位,所得图象的函数解析式为
的图象,再向上平移1个单位,所得图象的函数解析式为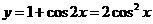 ,故选B.
,故选B.
答案:B
【命题立意】:本题考查三角函数的图象的平移和利用诱导公式及二倍角公式进行化简解析式的基本知识和基本技能,学会公式的变形.
4.【解析】:该空间几何体为一圆柱和一四棱锥组成的,圆柱的底面半径为1,高为2,体积为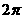 ,四棱锥的底面边长为
,四棱锥的底面边长为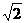 ,高为
,高为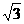 ,所以体积为
,所以体积为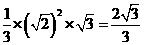 所以该几何体的体积为
所以该几何体的体积为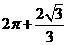 .答案:C
.答案:C
【命题立意】:本题考查了立体几何中的空间想象能力,
由三视图能够想象得到空间的立体图,并能准确地
计算出.几何体的体积.
5.【解析】:由平面与平面垂直的判定定理知如果m为平面α内的
一条直线, ,则
,则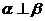 ,反过来则不一定.所以“
,反过来则不一定.所以“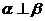 ”是“
”是“ ”的必要不充分条件.
”的必要不充分条件.
答案:B.
6.【解析】:函数有意义,需使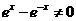 ,其定义域为
,其定义域为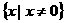 ,排除C,D,又因为
,排除C,D,又因为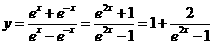 ,所以当
,所以当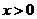 时函数为减函数,故选A.
时函数为减函数,故选A. 
答案:A.
【命题立意】:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.
7.【解析】:因为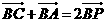 ,所以点P为线段AC的中点,所以应该选B。
,所以点P为线段AC的中点,所以应该选B。
答案:B。
【命题立意】:本题考查了向量的加法运算和平行四边形法则,可以借助图形解答。
8. 【解析】:产品净重小于100克的概率为(0.050+0.100)×2=0.300, 已知样本中产品净重小于100克的个数是36,设样本容量为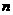 ,则
,则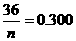 ,所以
,所以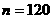 ,净重大于或等于98克并且小于104克的产品的概率为(0.100+0.150+0.125)×2=0.75,所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.75=90.故选A.
,净重大于或等于98克并且小于104克的产品的概率为(0.100+0.150+0.125)×2=0.75,所以样本中净重大于或等于98克并且小于104克的产品的个数是120×0.75=90.故选A.
答案:A
9. 【解析】:双曲线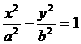 的一条渐近线为
的一条渐近线为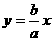 ,由方程组
,由方程组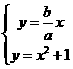 ,消去y,得
,消去y,得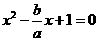 有唯一解,所以△=
有唯一解,所以△=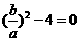 ,
,
所以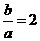 ,
,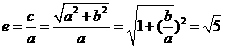 ,故选D.
,故选D.
答案:D.
10. 【解析】:由已知得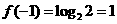 ,
,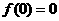 ,
,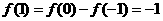 ,
,
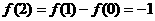 ,
,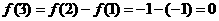 ,
,
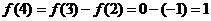 ,
,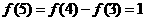 ,
,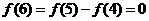 ,
,
所以函数f(x)的值以6为周期重复性出现.,所以f(2009)= f(5)=1,故选C.
答案:C.
11. 【解析】:在区间[-1,1]上随机取一个数x,即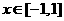 时,要使
时,要使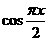 的值介于0到
的值介于0到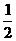 之间,需使
之间,需使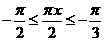 或
或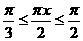 ∴
∴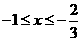 或
或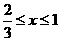 ,区间长度为
,区间长度为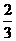 ,由几何概型知
,由几何概型知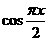 的值介于0到
的值介于0到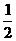 之间的概率为
之间的概率为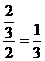 .故选A.
.故选A.
12. 【解析】:不等式表示的平面区域如图所示阴影部分,当直线ax+by= z(a>0,b>0)
过直线x-y+2=0与直线3x-y-6=0的交点(4,6)时,
目标函数z=ax+by(a>0,b>0)取得最大12,
即4a+6b=12,即2a+3b=6, 而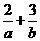 =
=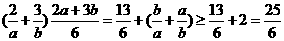 ,故选A.
,故选A.
答案:A
二、填空题
13. 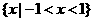 14.
14. 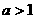 15.30 16. -8
15.30 16. -8
三、解答题
17. 解: (1)f(x)=cos(2x+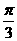 )+sin
)+sin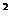 x.=
x.=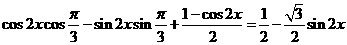
所以函数f(x)的最大值为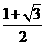 ,最小正周期
,最小正周期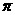 .
.
(2)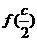 =
=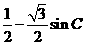 =-
=-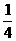 , 所以
, 所以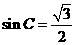 , 因为C为锐角, 所以
, 因为C为锐角, 所以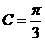 ,
,
又因为在 ABC 中, cosB=
ABC 中, cosB=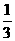 , 所以
, 所以 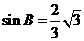 , 所以
, 所以
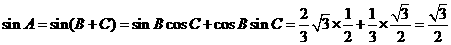 .
.
18. 解法一:(1)在直四棱柱ABCD-A B
B C
C D
D 中,取A1B1的中点F1,
中,取A1B1的中点F1,
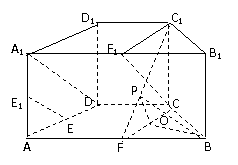
连接A1D,C1F1,CF1,因为AB=4, CD=2,且AB//CD,
所以CDA1F1,A1F1CD为平行四边形,所以CF1//A1D,
又因为E、E 分别是棱AD、AA
分别是棱AD、AA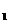 的中点,所以EE1//A1D,
的中点,所以EE1//A1D,
所以CF1//EE1,又因为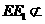 平面FCC
平面FCC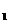 ,
,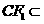 平面FCC
平面FCC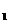 ,
,
所以直线EE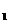 //平面FCC
//平面FCC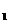 .
.
(2)因为AB=4, BC=CD=2, 、F是棱AB的中点,所以BF=BC=CF,△BCF为正三角形,取CF的中点O,则OB⊥CF,又因为直四棱柱ABCD-A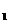 B
B C
C D
D 中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC
中,CC1⊥平面ABCD,所以CC1⊥BO,所以OB⊥平面CC1F,过O在平面CC1F内作OP⊥C1F,垂足为P,连接BP,则∠OPB为二面角B-FC -C的一个平面角, 在△BCF为正三角形中,
-C的一个平面角, 在△BCF为正三角形中,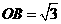 ,在Rt△CC1F中, △OPF∽△CC1F,∵
,在Rt△CC1F中, △OPF∽△CC1F,∵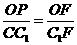 ∴
∴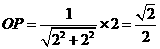 ,
,
在Rt△OPF中,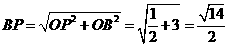 ,
,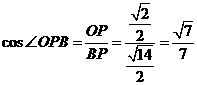 ,
,
所以二面角B-FC -C的余弦值为
-C的余弦值为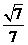 .
.
解法二:(1)因为AB=4, BC=CD=2, F是棱AB的中点,
所以BF=BC=CF,△BCF为正三角形, 因为ABCD为
等腰梯形,所以∠BAC=∠ABC=60°,取AF的中点M,
连接DM,则DM⊥AB,所以DM⊥CD,
以DM为x轴,DC为y轴,DD1为z轴建立空间直角坐标系,
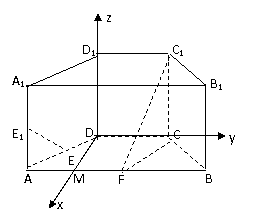
,则D(0,0,0),A(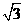 ,-1,0),F(
,-1,0),F(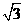 ,1,0),C(0,2,0),
,1,0),C(0,2,0),
C1(0,2,2),E(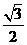 ,
,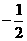 ,0),E1(
,0),E1(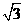 ,-1,1),所以
,-1,1),所以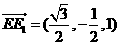 ,
,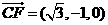 ,
,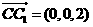
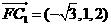 设平面CC1F的法向量为
设平面CC1F的法向量为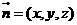 则
则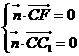 所以
所以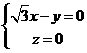 取
取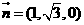 ,则
,则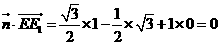 ,所以
,所以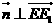 ,所以直线EE
,所以直线EE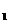 //平面FCC
//平面FCC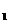 .
.
(2)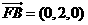 ,设平面BFC1的法向量为
,设平面BFC1的法向量为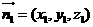 ,则
,则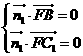 所以
所以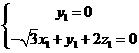 ,取
,取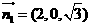 ,则
,则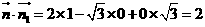 ,
,
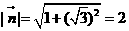 ,
,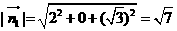 ,
,
所以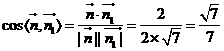 ,由图可知二面角B-FC
,由图可知二面角B-FC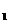 -C为锐角,所以二面角B-FC
-C为锐角,所以二面角B-FC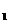 -C的余弦值为
-C的余弦值为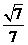 .
. 
19. 解:(1)设该同学在A处投中为事件A,在B处投中为事件B,则事件A,B相互独立,且P(A)=0.25,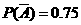 , P(B)= q
, P(B)= q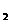 ,
,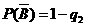 .
.
根据分布列知: 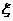 =0时
=0时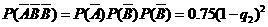 =0.03,所以
=0.03,所以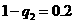 ,q
,q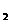 =0.8.
=0.8.
(2)当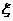 =2时, P1=
=2时, P1=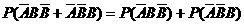
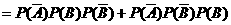 =0.75 q
=0.75 q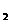 (
( 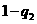 )×2=1.5 q
)×2=1.5 q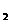 (
( 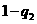 )=0.24
)=0.24
当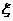 =3时, P2 =
=3时, P2 =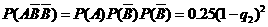 =0.01,
=0.01,
当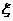 =4时, P3=
=4时, P3=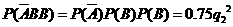 =0.48,
=0.48,
当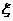 =5时, P4=
=5时, P4=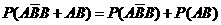
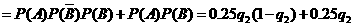 =0.24
=0.24
所以随机变量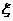 的分布列为
的分布列为
| 0 | 2 | 3 | 4 | 5 |
p | 0.03 | 0.24 | 0.01 | 0.48 | 0.24 |
随机变量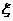 的数学期望
的数学期望
(3)该同学选择都在B处投篮得分超过3分的概率为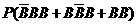
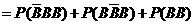
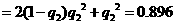 ;
;
该同学选择(1)中方式投篮得分超过3分的概率为0.48+0.24=0.72.
由此看来该同学选择都在B处投篮得分超过3分的概率大.
20. 解:因为对任意的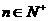 ,点
,点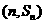 ,均在函数
,均在函数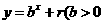 且
且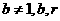 均为常数的图像上.所以得
均为常数的图像上.所以得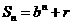 ,当
,当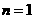 时,
时,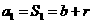 ,当
,当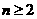 时,
时,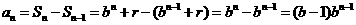 ,又因为{
,又因为{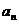 }为等比数列,所以
}为等比数列,所以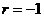 ,公比为
,公比为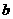 ,
,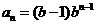
(2)当b=2时,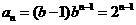 ,
, 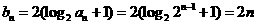
则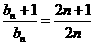 ,所以
,所以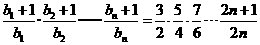
下面用数学归纳法证明不等式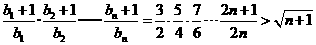 成立.
成立.
① 当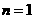 时,左边=
时,左边=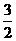 ,右边=
,右边=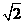 ,因为
,因为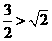 ,所以不等式成立.
,所以不等式成立.
② 假设当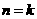 时不等式成立,即
时不等式成立,即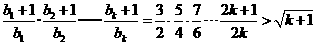 成立.则当
成立.则当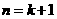 时,左边=
时,左边=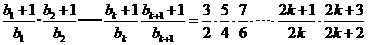
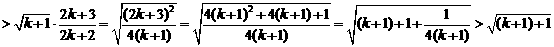
所以当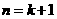 时,不等式也成立.
时,不等式也成立.
由①、②可得不等式恒成立.
21. 解法一:
(1)如图,由题意知AC⊥BC,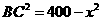 ,
,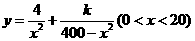
其中当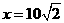 时,y=0.065,所以k=9
时,y=0.065,所以k=9
所以y表示成x的函数为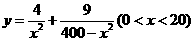
(2)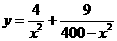 ,
,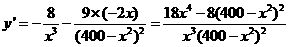 ,令
,令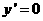 得
得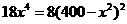 ,所以
,所以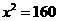 ,即
,即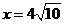 ,当
,当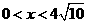 时,
时, 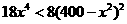 ,即
,即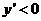 所以函数为单调减函数,当
所以函数为单调减函数,当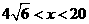 时,
时, 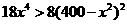 ,即
,即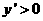 所以函数为单调增函数.所以当
所以函数为单调增函数.所以当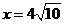 时, 即当C点到城A的距离为
时, 即当C点到城A的距离为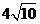 时, 函数
时, 函数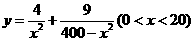 有最小值.
有最小值.
解法二: (1)同上.
(2)设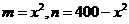 ,
,
则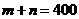 ,
,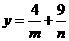 ,所以
,所以
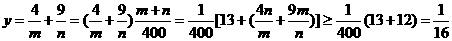 当且仅当
当且仅当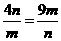 即
即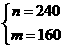 时取”=”.
时取”=”.
下面证明函数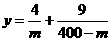 在(0,160)上为减函数, 在(160,400)上为增函数.
在(0,160)上为减函数, 在(160,400)上为增函数.
设0<m1<m2<160,则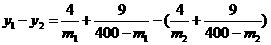
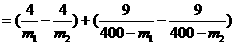
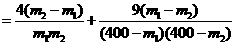
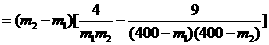
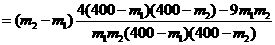 ,
,
因为0<m1<m2<160,所以4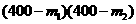 >4×240×240
>4×240×240
9 m1m2<9×160×160所以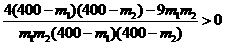 ,
,
所以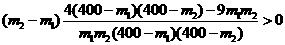 即
即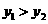 函数
函数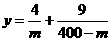 在(0,160)上为减函数.
在(0,160)上为减函数.
同理,函数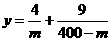 在(160,400)上为增函数,设160<m1<m2<400,则
在(160,400)上为增函数,设160<m1<m2<400,则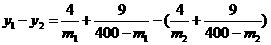
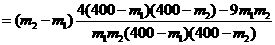
因为1600<m1<m2<400,所以4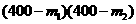 <4×240×240, 9 m1m2>9×160×160
<4×240×240, 9 m1m2>9×160×160
所以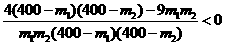 ,
,
所以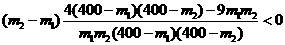 即
即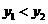 函数
函数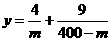 在(160,400)上为增函数.
在(160,400)上为增函数.
所以当m=160即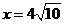 时取”=”,函数y有最小值,
时取”=”,函数y有最小值,
所以弧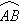 上存在一点,当
上存在一点,当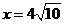 时使建在此处的垃圾处理厂对城A和城B的总影响度最小.
时使建在此处的垃圾处理厂对城A和城B的总影响度最小.
22. 解:(1)因为椭圆E: 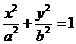 (a,b>0)过M(2,
(a,b>0)过M(2,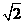 ) ,N(
) ,N(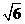 ,1)两点,
,1)两点,
所以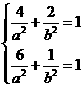 解得
解得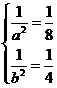 所以
所以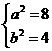 椭圆E的方程为
椭圆E的方程为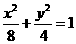
(2)假设存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且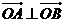 ,设该圆的切线方程为
,设该圆的切线方程为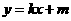 解方程组
解方程组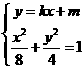 得
得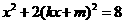 ,即
,即 ,
,
则△=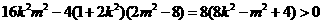 ,即
,即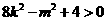
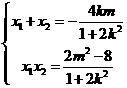 ,
,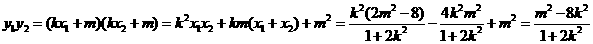 要使
要使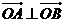 ,需使
,需使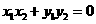 ,即
,即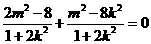 ,所以
,所以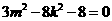 ,所以
,所以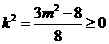 又
又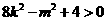 ,所以
,所以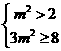 ,所以
,所以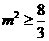 ,即
,即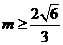 或
或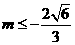 ,因为直线
,因为直线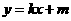 为圆心在原点的圆的一条切线,所以圆的半径为
为圆心在原点的圆的一条切线,所以圆的半径为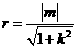 ,
,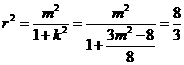 ,
,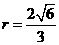 ,所求的圆为
,所求的圆为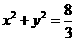 ,此时圆的切线
,此时圆的切线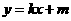 都满足
都满足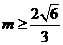 或
或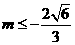 ,而当切线的斜率不存在时切线为
,而当切线的斜率不存在时切线为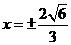 与椭圆
与椭圆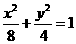 的两个交点为
的两个交点为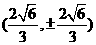 或
或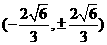 满足
满足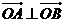 ,综上, 存在圆心在原点的圆
,综上, 存在圆心在原点的圆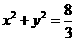 ,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且
,使得该圆的任意一条切线与椭圆E恒有两个交点A,B,且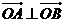 .
.
因为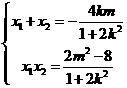 ,
,
所以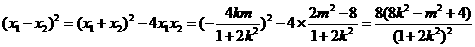 ,
,
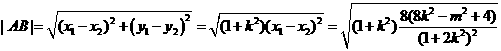
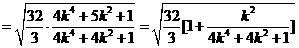 ,
,
①当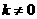 时
时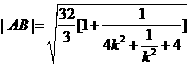
因为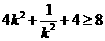 所以
所以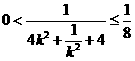 ,
,
所以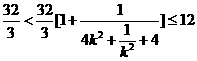 ,
,
所以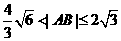 当且仅当
当且仅当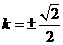 时取”=”.
时取”=”.
② 当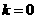 时,
时,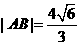 .
.
③ 当AB的斜率不存在时, 两个交点为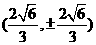 或
或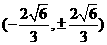 ,所以此时
,所以此时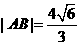 ,
,
综上, |AB |的取值范围为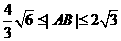 即:
即: