(单词翻译:单击)
第Ⅰ卷(共60分)
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)若复数z满足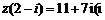 为虚数单位),则
为虚数单位),则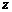 为
为
(A)3+5i (B)3-5i(C)-3+5i (D)-3-5i
【解析】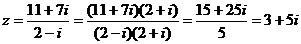 .故选A.
.故选A.
【答案】A
(2)已知全集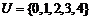 ,集合
,集合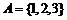 ,
,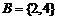 ,则
,则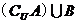 为
为
(A){1,2,4}(B){2,3,4}(C){0,2,4}(D){0,2,3,4}
【解析】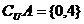 ,所以
,所以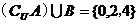 ,选C.
,选C.
【答案】C
(3)函数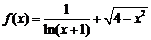 的定义域为
的定义域为
(A)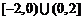 (B)
(B)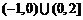 (C)
(C)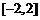 (D)
(D)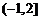
【解析】要使函数有意义则有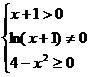 ,即
,即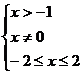 ,即
,即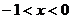 或
或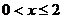 ,选B.
,选B.
【答案】B
(4)在某次测量中得到的A样本数据如下:82,84,84,86,86,86,88,88,88,88.若B样本数据恰好是A样本数据都加2后所得数据,则A,B两样本的下列数字特征对应相同的是
(A)众数 (B)平均数 (C)中位数 (D)标准差
【解析】设A样本的数据为变量为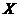 ,B样本的数据为变量为
,B样本的数据为变量为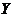 ,则满足
,则满足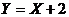 ,根据方差公式可得
,根据方差公式可得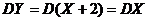 ,所以方差相同,标准差也相同,选D.
,所以方差相同,标准差也相同,选D.
【答案】D
(5)设命题p:函数 的最小正周期为
的最小正周期为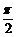 ;命题q:函数
;命题q:函数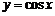 的图象关于直线
的图象关于直线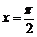 对称.则下列判断正确的是
对称.则下列判断正确的是
(A)p为真 (B)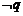 为假 (C)
为假 (C)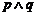 为假 (D)
为假 (D)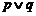 为真
为真
【解析】函数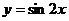 的周期为
的周期为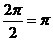 ,所以命题
,所以命题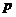 为假;函数
为假;函数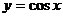 的对称轴为
的对称轴为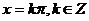 ,所以命题
,所以命题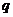 为假,所以
为假,所以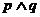 为假,选C.
为假,选C.
【答案】C
(6)设变量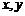 满足约束条件
满足约束条件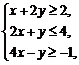 则目标函数
则目标函数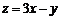 的取值范围是
的取值范围是
(A)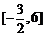 (B)
(B)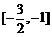 (C)
(C)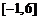 (D)
(D)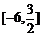
【解析】做出不等式所表示的区域如图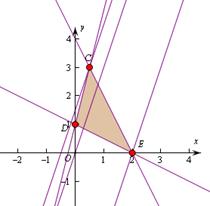 ,由
,由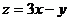 得
得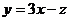 ,平移直线
,平移直线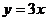 ,由图象可知当直线经过点
,由图象可知当直线经过点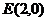 时,直线
时,直线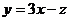 的截距最小,此时
的截距最小,此时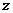 最大为
最大为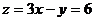 ,当直线经过
,当直线经过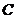 点时,直线截距最大,此时
点时,直线截距最大,此时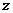 最小,由
最小,由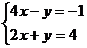 ,解得
,解得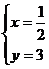 ,此时
,此时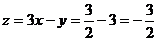 ,所以
,所以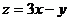 的取值范围是
的取值范围是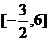 ,选A.
,选A.
【答案】A
(7)执行右面的程序框图,如果输入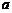 =4,那么输出的n的值为
=4,那么输出的n的值为
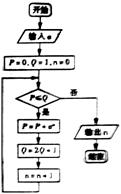
(A)2 (B)3 (C)4 (D)5
【解析】当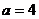 时,第一次
时,第一次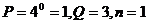 ,第二次
,第二次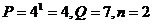 ,第三次
,第三次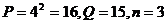 ,此时
,此时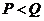 不满足,输出
不满足,输出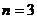 ,选B.
,选B.
【答案】B
(8)函数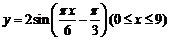 的最大值与最小值之和为
的最大值与最小值之和为
(A)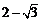 (B)0 (C)-1 (D)
(B)0 (C)-1 (D)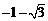
【解析】因为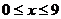 ,所以
,所以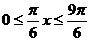 ,
,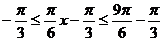 ,即
,即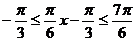 ,所以当
,所以当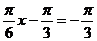 时,最小值为
时,最小值为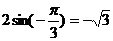 ,当
,当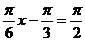 时,最大值为
时,最大值为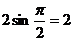 ,所以最大值与最小值之和为
,所以最大值与最小值之和为 ,选A.
,选A.
【答案】A
(9)圆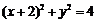 与圆
与圆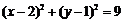 的位置关系为
的位置关系为
(A)内切 (B)相交 (C)外切 (D)相离
【解析】两圆的圆心分别为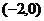 ,
,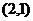 ,半径分别为
,半径分别为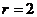 ,
,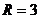 两圆的圆心距离为
两圆的圆心距离为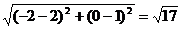 ,则
,则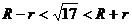 ,所以两圆相交,选B.
,所以两圆相交,选B.
【答案】B
(10)函数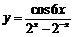 的图象大致为
的图象大致为

【解析】函数为奇函数,所以图象关于原点对称,排除A,令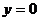 得
得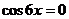 ,所以
,所以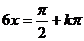 ,
,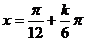 ,函数零点有无穷多个,排除C,且
,函数零点有无穷多个,排除C,且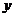 轴右侧第一个零点为
轴右侧第一个零点为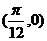 ,又函数
,又函数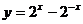 为增函数,当
为增函数,当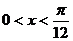 时,
时,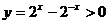 ,
,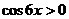 ,所以函数
,所以函数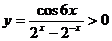 ,排除B,选D.
,排除B,选D.
【答案】D
(11)已知双曲线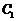 :
: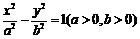 的离心率为2.若抛物线
的离心率为2.若抛物线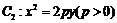 的焦点到双曲线
的焦点到双曲线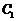 的渐近线的距离为2,则抛物线
的渐近线的距离为2,则抛物线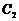 的方程为
的方程为
(A) 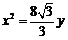 (B)
(B) 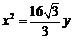 (C)
(C)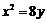 (D)
(D)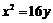
【解析】抛物线的焦点 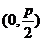 ,双曲线的渐近线为
,双曲线的渐近线为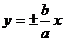 ,不妨取
,不妨取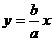 ,即
,即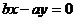 ,焦点到渐近线的距离为
,焦点到渐近线的距离为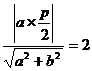 ,即
,即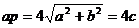 ,所以
,所以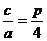 双曲线的离心率为
双曲线的离心率为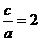 ,所以
,所以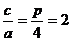 ,所以
,所以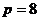 ,所以抛物线方程为
,所以抛物线方程为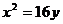 ,选D.
,选D.
【答案】D
(12)设函数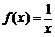 ,
,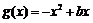 .若
.若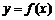 的图象与
的图象与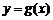 的图象有且仅有两个不同的公共点
的图象有且仅有两个不同的公共点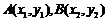 ,则下列判断正确的是
,则下列判断正确的是
(A)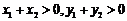 (B)
(B)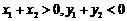
(C)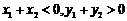 (D)
(D)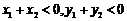
【解析】方法一:在同一坐标系中分别画出两个函数的图象,要想满足条件,则有如图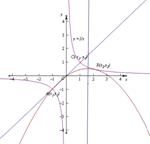 ,做出点A关于原点的对称点C,则C点坐标为
,做出点A关于原点的对称点C,则C点坐标为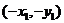 ,由图象知
,由图象知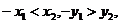 即
即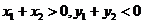 ,故答案选B.
,故答案选B.
方法二:设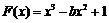 ,则方程
,则方程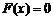 与
与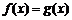 同解,故其有且仅有两个不同零点
同解,故其有且仅有两个不同零点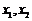 .由
.由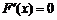 得
得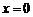 或
或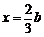 .这样,必须且只须
.这样,必须且只须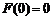 或
或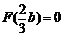 ,因为
,因为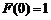 ,故必有
,故必有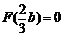 由此得
由此得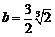 .不妨设
.不妨设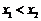 ,则
,则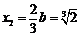 .所以
.所以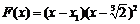 ,比较系数得
,比较系数得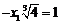 ,故
,故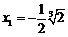 .
.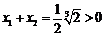 ,由此知
,由此知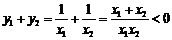 ,故答案为B.
,故答案为B.
【答案】B
第Ⅱ卷(共90分)
二、填空题:本大题共4小题,每小题4分,共16分.
(13)如图,正方体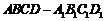 的棱长为1,E为线段
的棱长为1,E为线段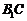 上的一点,则三棱锥
上的一点,则三棱锥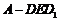 的体积为_____.
的体积为_____.
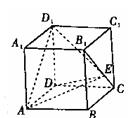
【解析】以△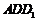 为底面,则易知三棱锥的高为1,故
为底面,则易知三棱锥的高为1,故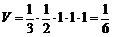 .
.
【答案】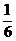
(14)右图是根据部分城市某年6月份的平均气温(单位:℃)数据得到的样本频率分布直方图,其中平均气温的范围是[20.5,26.5],样本数据的分组为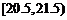 ,
,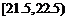 ,
,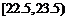 ,
,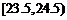 ,
,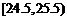 ,
, .已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为____.
.已知样本中平均气温低于22.5℃的城市个数为11,则样本中平均气温不低于25.5℃的城市个数为____.
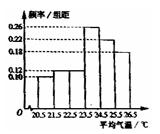
【解析】最左边两个矩形面积之和为0.10×1+0.12×1=0.22,总城市数为11÷0.22=50,最右面矩形面积为0.18×1=0.18,50×0.18=9.
【答案】9
(15)若函数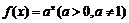 在[-1,2]上的最大值为4,最小值为m,且函数
在[-1,2]上的最大值为4,最小值为m,且函数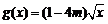 在
在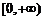 上是增函数,则a=____.
上是增函数,则a=____.
【解析】当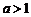 时,有
时,有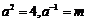 ,此时
,此时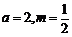 ,此时
,此时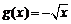 为减函数,不合题意.若
为减函数,不合题意.若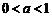 ,则
,则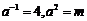 ,故
,故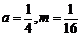 ,检验知符合题意.
,检验知符合题意.
【答案】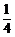
(16)如图,在平面直角坐标系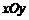 中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,
中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P的位置在(0,0),圆在x轴上沿正向滚动.当圆滚动到圆心位于(2,1)时,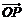 的坐标为____.
的坐标为____. 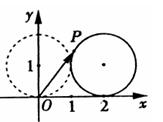
【解析】因为圆心移动的距离为2,所以劣弧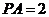 ,即圆心角
,即圆心角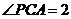 ,
,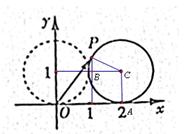 ,则
,则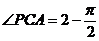 ,所以
,所以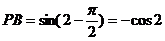 ,
,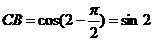 ,所以
,所以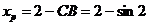 ,
,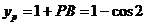 ,所以
,所以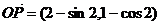 .
.
另解:根据题意可知滚动制圆心为(2,1)时的圆的参数方程为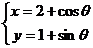 ,且
,且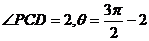 ,则点P的坐标为
,则点P的坐标为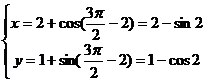 ,即
,即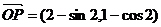 .
.
【答案】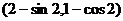
三、解答题:本大题共6小题,共74分.
(17)(本小题满分12分)
在△ABC中,内角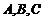 所对的边分别为
所对的边分别为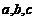 ,已知
,已知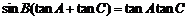 .
.
(Ⅰ)求证: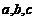 成等比数列;
成等比数列;
(Ⅱ)若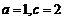 ,求△
,求△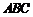 的面积S.
的面积S.
【答案】(17)(I)由已知得:
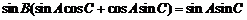 ,
,
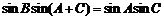 ,
,
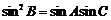 ,
,
再由正弦定理可得: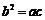 ,
,
所以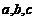 成等比数列.
成等比数列.
(II)若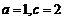 ,则
,则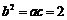 ,
,
∴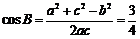 ,
,
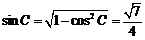 ,
,
∴△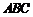 的面积
的面积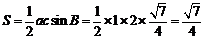 .
.
(18)(本小题满分12分)
袋中有五张卡片,其中红色卡片三张,标号分别为1,2,3;蓝色卡片两张,标号分别为1,2.
(Ⅰ)从以上五张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率;
(Ⅱ)现袋中再放入一张标号为0的绿色卡片,从这六张卡片中任取两张,求这两张卡片颜色不同且标号之和小于4的概率.
【答案】(18)(I)从五张卡片中任取两张的所有可能情况有如下10种:红1红2,红1红3,红1蓝1,红1蓝2,红2红3,红2蓝1,红2蓝2,红3蓝1,红3蓝2,蓝1蓝2.其中两张卡片的颜色不同且标号之和小于4的有3种情况,故所求的概率为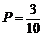 .
.
(II)加入一张标号为0的绿色卡片后,从六张卡片中任取两张,除上面的10种情况外,多出5种情况:红1绿0,红2绿0,红3绿0,蓝1绿0,蓝2绿0,即共有15种情况,其中颜色不同且标号之和小于4的有8种情况,所以概率为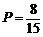 .
.
(19) (本小题满分12分)
如图,几何体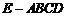 是四棱锥,△
是四棱锥,△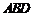 为正三角形,
为正三角形,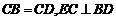 .
.
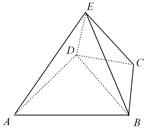
(Ⅰ)求证: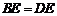 ;
;
(Ⅱ)若∠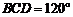 ,M为线段AE的中点,求证:
,M为线段AE的中点,求证: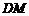 ∥平面
∥平面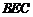 .
.
【答案】(19)(I)设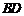 中点为O,连接OC,OE,则由
中点为O,连接OC,OE,则由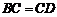 知
知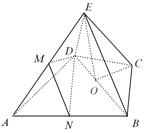 ,
,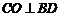 ,
,
又已知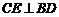 ,所以
,所以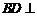 平面OCE.
平面OCE.
所以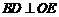 ,即OE是BD的垂直平分线,
,即OE是BD的垂直平分线,
所以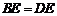 .
.
(II)取AB中点N,连接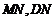 ,
,
∵M是AE的中点,∴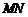 ∥
∥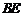 ,
,
∵△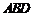 是等边三角形,∴
是等边三角形,∴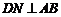 .
.
由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即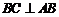 ,
,
所以ND∥BC,
所以平面MND∥平面BEC,故DM∥平面BEC.
(20) (本小题满分12分)
已知等差数列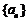 的前5项和为105,且
的前5项和为105,且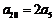 .
.
(Ⅰ)求数列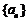 的通项公式;
的通项公式;
(Ⅱ)对任意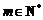 ,将数列
,将数列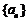 中不大于
中不大于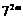 的项的个数记为
的项的个数记为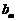 .求数列
.求数列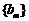 的前m项和
的前m项和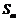 .
.
【答案】 (I)由已知得: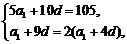
解得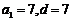 ,
,
所以通项公式为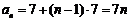 .
.
(II)由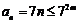 ,得
,得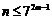 ,
,
即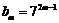 .
.
∵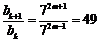 ,
,
∴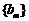 是公比为49的等比数列,
是公比为49的等比数列,
∴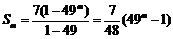 .
.
(21) (本小题满分13分)
如图,椭圆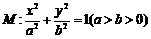 的离心率为
的离心率为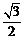 ,直线
,直线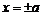 和
和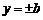 所围成的矩形ABCD的面积为8.
所围成的矩形ABCD的面积为8.
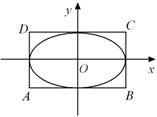
(Ⅰ)求椭圆M的标准方程;
(Ⅱ) 设直线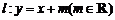 与椭圆M有两个不同的交点
与椭圆M有两个不同的交点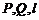 与矩形ABCD有两个不同的交点
与矩形ABCD有两个不同的交点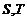 .求
.求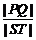 的最大值及取得最大值时m的值.
的最大值及取得最大值时m的值.
【答案】(21)(I)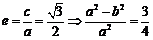 ……①
……①
矩形ABCD面积为8,即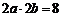 ……②
……②
由①②解得: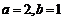 ,
,
∴椭圆M的标准方程是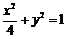 .
.
(II)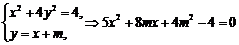 ,
,
设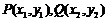 ,则
,则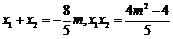 ,
,
由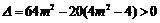 得
得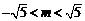 .
.
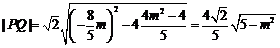 .
.
当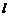 过
过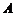 点时,
点时,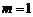 ,当
,当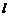 过
过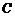 点时,
点时,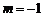 .
.
①当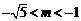 时,有
时,有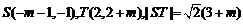 ,
,
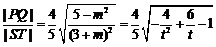 ,
,
其中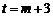 ,由此知当
,由此知当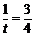 ,即
,即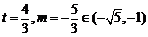 时,
时,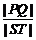 取得最大值
取得最大值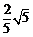 .
.
②由对称性,可知若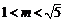 ,则当
,则当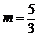 时,
时,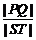 取得最大值
取得最大值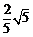 .
.
③当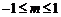 时,
时,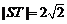 ,
,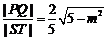 ,
,
由此知,当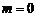 时,
时,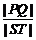 取得最大值
取得最大值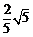 .
.
综上可知,当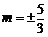 和0时,
和0时,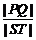 取得最大值
取得最大值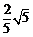 .
.
(22) (本小题满分13分)
已知函数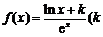 为常数,e=2.71828…是自然对数的底数),曲线
为常数,e=2.71828…是自然对数的底数),曲线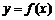 在点
在点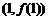 处的切线与x轴平行.
处的切线与x轴平行.
(Ⅰ)求k的值;
(Ⅱ)求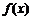 的单调区间;
的单调区间;
(Ⅲ)设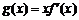 ,其中
,其中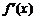 为
为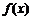 的导函数.证明:对任意
的导函数.证明:对任意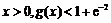 .
.
【答案】
(I)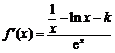 ,
,
由已知,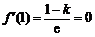 ,∴
,∴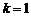 .
.
(II)由(I)知,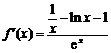 .
.
设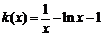 ,则
,则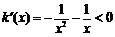 ,即
,即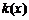 在
在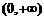 上是减函数,
上是减函数,
由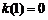 知,当
知,当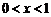 时
时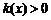 ,从而
,从而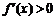 ,
,
当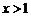 时
时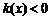 ,从而
,从而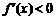 .
.
综上可知,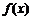 的单调递增区间是
的单调递增区间是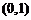 ,单调递减区间是
,单调递减区间是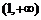 .
.
(III)由(II)可知,当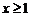 时,
时,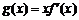 ≤0<1+
≤0<1+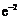 ,故只需证明
,故只需证明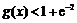 在
在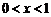 时成立.
时成立.
当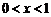 时,
时,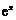 >1,且
>1,且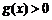 ,∴
,∴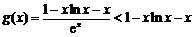 .
.
设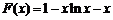 ,
,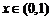 ,则
,则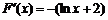 ,
,
当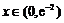 时,
时,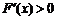 ,当
,当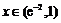 时,
时,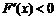 ,
,
所以当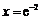 时,
时,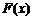 取得最大值
取得最大值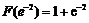 .
.
所以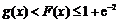 .
.
综上,对任意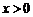 ,
,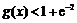 .
.


