(单词翻译:单击)
一.选择题:本题共12个小题,每题5分,共60分。
(1)、复数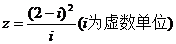 ,则
,则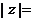
(A)25 (B) 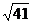 (C)6 (D)
(C)6 (D) 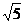

(2)、已知集合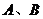 均为全集
均为全集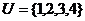 的子集,且
的子集,且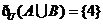 ,
,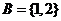 ,则
,则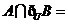
(A){3} (B){4} (C){3,4} (D)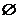

(3)、已知函数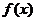 为奇函数,且当
为奇函数,且当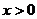 时,
时,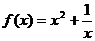 ,
,
则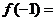
(A)2 (B)1 (C)0 (D)-2】

(4)、一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如右图所示该四棱锥侧面积和体积分别是
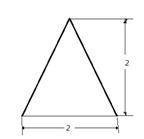
(A)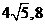 (B)
(B) 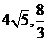 (C)
(C) 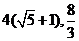 (D) 8,8
(D) 8,8

(5)、函数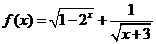 的定义域为
的定义域为
(A)(-3,0] (B) (-3,1]
(C) 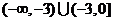 (D)
(D) 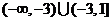

(6)、执行右边的程序框图,若第一次输入的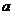 的值为-1.2,第二次输入的
的值为-1.2,第二次输入的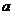 的值为1.2,则第一次、
的值为1.2,则第一次、
第二次输出的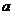 的值分别为
的值分别为
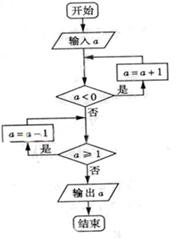
(A)0.2,0.2 (B) 0.2,0.8
(C) 0.8,0.2 (D) 0.8,0.8

(7)、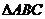 的内角
的内角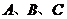 的对边分别是
的对边分别是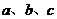 ,若
,若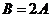 ,
,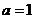 ,
,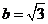 ,则
,则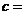
(A) 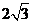 (B) 2 (C)
(B) 2 (C)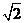 (D)1
(D)1

(8)、给定两个命题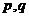 ,
,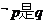 的必要而不充分条件,则
的必要而不充分条件,则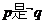
(A)充分而不必要条件 (B)必要而不充分条件 (C)充要条件 (D)既不充分也不必要条件

(9)、函数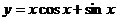 的图象大致为
的图象大致为
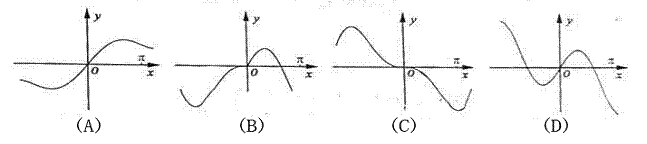

(10)、将某选手的9个得分去掉1个最高分,去掉1个最低分,7个剩余分数的平均分为91,现场做的9个分数的茎叶图后来有一个数据模糊,无法辨认,在图中以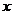 表示:
表示:
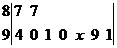
则7个剩余分数的方差为
(A)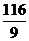 (B)
(B)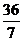 (C)36 (D)
(C)36 (D) 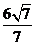

(11)、抛物线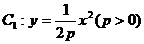 的焦点与双曲线
的焦点与双曲线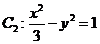 的右焦点的连线交
的右焦点的连线交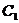 于第一象限的点M,若
于第一象限的点M,若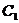 在点M处的切线平行于
在点M处的切线平行于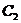 的一条渐近线,则
的一条渐近线,则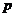 =
=
(A)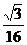 (B)
(B)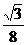 (C)
(C)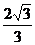 (D)
(D) 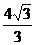


(12)、设正实数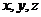 满足
满足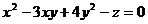 ,则当
,则当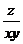 取得最大值时,
取得最大值时,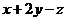 的最大值为
的最大值为
(A)0 (B)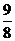 (C)2 (D)
(C)2 (D)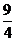

二.填空题:本大题共4小题,每小题4分,共16分
(13)、过点(3,1)作圆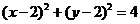 的弦,其中最短的弦长为__________
的弦,其中最短的弦长为__________

(14)、在平面直角坐标系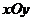 中,
中,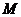 为不等式组
为不等式组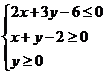 所表示的区域上一动点,则直线
所表示的区域上一动点,则直线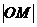 的最小值为_______
的最小值为_______

(15)、在平面直角坐标系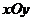 中,已知
中,已知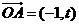 ,
,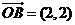 ,若
,若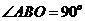 ,则实数
,则实数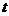 的值为______
的值为______

(16).定义“正对数”: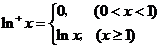 ,
,
现有四个命题:
①若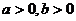 ,则
,则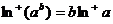 ;
;
②若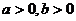 ,则
,则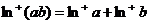
③若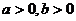 ,则
,则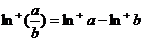
④若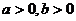 ,则
,则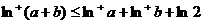
其中的真命题有____________(写出所有真命题的序号)


三.解答题:本大题共6小题,共74分,
(17)(本小题满分12分)
某小组共有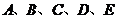 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)
如下表所示:
A | B | C | D | E | |
身高 | 1.69 | 1.73 | 1.75 | 1.79 | 1.82 |
体重指标 | 19.2 | 25.1 | 18.5 | 23.3 | 20.9 |
(Ⅰ)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率
(Ⅱ)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率

(18)(本小题满分12分)
设函数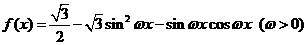 ,且
,且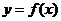 的图象的一个对称中心到最近的对称轴的距离为
的图象的一个对称中心到最近的对称轴的距离为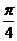 ,
,
(Ⅰ)求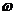 的值
的值
(Ⅱ)求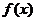 在区间
在区间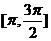 上的最大值和最小值
上的最大值和最小值
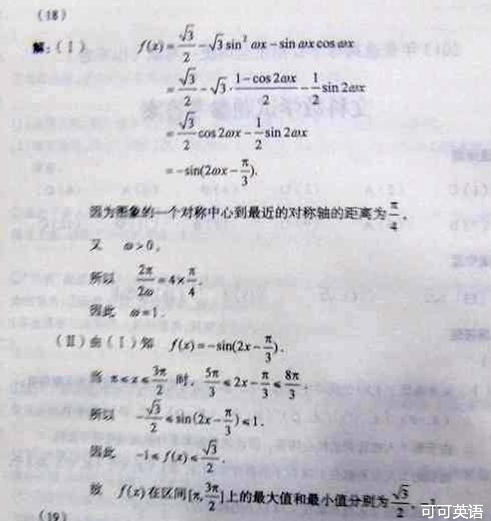
(19)(本小题满分12分)
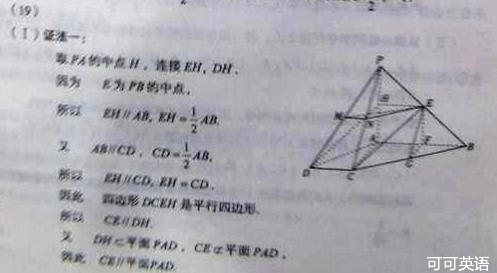
如图,四棱锥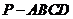 中,
中,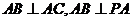 ,
,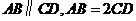 ,
,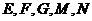 分别为
分别为
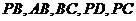 的中点
的中点
(Ⅰ)求证: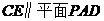
(Ⅱ)求证: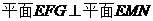

(20)(本小题满分12分)
设等差数列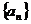 的前
的前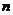 项和为
项和为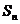 ,且
,且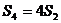 ,
,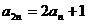
(Ⅰ)求数列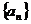 的通项公式
的通项公式
(Ⅱ)设数列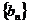 满足
满足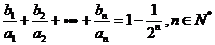 ,求
,求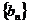 的前
的前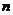 项和
项和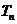

(21)(本小题满分12分)
已知函数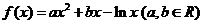
(Ⅰ)设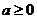 ,求
,求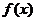 的单调区间
的单调区间
(Ⅱ) 设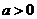 ,且对于任意
,且对于任意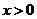 ,
,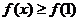 。试比较
。试比较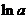 与
与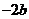 的大小
的大小


(22)(本小题满分14分)
在平面直角坐标系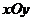 中,已知椭圆C的中心在原点O,焦点在
中,已知椭圆C的中心在原点O,焦点在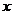 轴上,短轴长为2,离心率为
轴上,短轴长为2,离心率为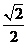
(I)求椭圆C的方程
(II)A,B为椭圆C上满足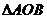 的面积为
的面积为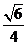 的任意两点,E为线段AB的中点,射线OE交椭圆C与点P,设
的任意两点,E为线段AB的中点,射线OE交椭圆C与点P,设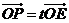 ,求实数
,求实数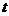 的值
的值





