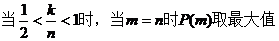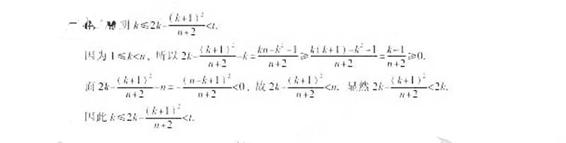(单词翻译:单击)
第Ⅰ卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1) 设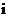 是虚数单位,
是虚数单位,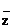 是复数
是复数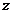 的共轭复数,若
的共轭复数,若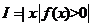
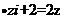 ,则
,则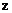 =
=
(A)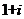 (B)
(B)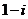
(C)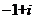 (D)
(D)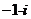
【答案】A
【解析】设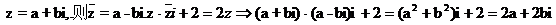
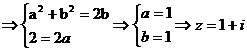
所以选A
(2) 如图所示,程序框图(算法流程图)的输出结果是
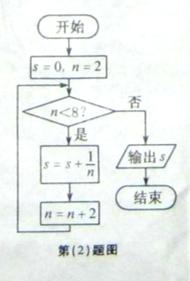
(A) 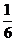 (B)
(B)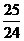
(C)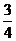 (D)
(D)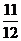
【答案】D
【解析】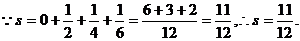 ,所以选D
,所以选D
(3)在下列命题中,不是公理的是
(A)平行于同一个平面的两个平面相互平行
(B)过不在同一条直线上的三点,有且只有一个平面
(C)如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内
(D)如果两个不重合的平面有一个公共点, 那么他们有且只有一条过该点的公共直线
【答案】A
【解析】B,C,D说法均不需证明,也无法证明,是公理;C选项可以推导证明,故是定理。
所以选A
(4)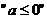 “是函数
“是函数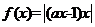 在区间
在区间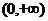 内单调递增”的
内单调递增”的
(A) 充分不必要条件 (B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
【答案】C
【解析】 当a=0 时,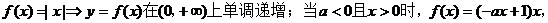
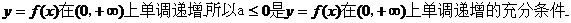
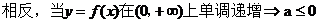 ,
,
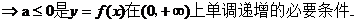
故前者是后者的充分必要条件。所以选C
(5)某班级有50名学生,其中有30名男生和20名女生,随机询问了该班五名男生和五名女生在某次数学测验中的成绩,五名男生的成绩分别为86,94,88,92,90,五名女生的成绩分别为88,93,93,88,93.下列说法一定正确的是
(A)这种抽样方法是一种分层抽样
(B)这种抽样方法是一种系统抽样
(C)这五名男生成绩的方差大于这五名女生成绩的方差
(D)该班级男生成绩的平均数小于该班女生成绩的平均数
【答案】C
【解析】 对A选项,分层抽样要求男女生总人数之比=男女生抽样人数之比,所以A选项错。
对B选项,系统抽样要求先对个体进行编号再抽样,所以B选项错。
对D选项,男生平均成绩为90,女生平均成绩为91。所以D选项错。
对C选项,男生方差为40,女生方差为30。所以C选项正确。
所以选C
(6)已知一元二次不等式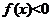 的解集为
的解集为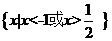 ,则
,则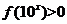 的解集为
的解集为
(A)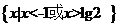 (B)
(B)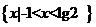
(C) 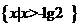 (D)
(D)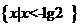
【答案】D
【解析】 由题知,一元二次不等式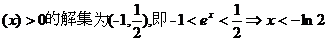
所以选D。
(7)在极坐标系中,圆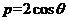 的垂直于极轴的两条切线方程分别为
的垂直于极轴的两条切线方程分别为
(A)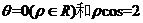 (B)
(B)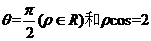
(C) 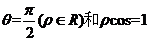 (D)
(D)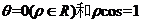
【答案】B
【解析】在极坐标系中,圆心坐标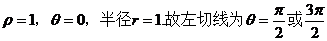
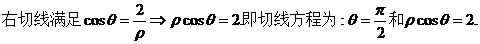
所以选B
(8)函数 的图像如图所示,在区间
的图像如图所示,在区间 上可找到
上可找到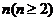
个不同的数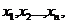 使得
使得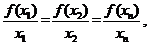 则
则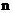 的取值范围是
的取值范围是
(A)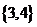 (B)
(B)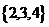
(C) 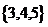 (D)
(D)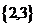
【答案】B
【解析】由题知,过原点的直线与曲线相交的个数即n的取值.用尺规作图,交点可取2,3,4.
所以选B
(9)在平面直角坐标系中,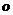 是坐标原点,两定点
是坐标原点,两定点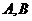 满足
满足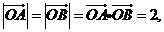 则点集
则点集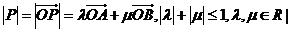 所表示的区域的面积是
所表示的区域的面积是
(A)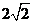 (B)
(B)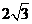
(C) 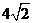 (D)
(D)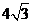
【答案】D
【解析】考察三点共线向量知识: 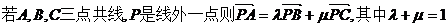 .
.
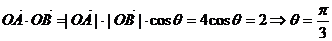 .建立直角坐标系,设A(2,0),
.建立直角坐标系,设A(2,0),
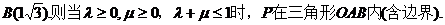
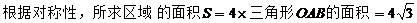
所以选D
(10)若函数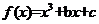 有极值点
有极值点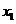 ,
,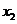 ,且
,且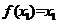 ,则关于
,则关于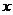 的方程
的方程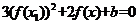 的不同实根个数是
的不同实根个数是
(A)3 (B)4
(C) 5 (D)6
【答案】 A
【解析】 使用代值法。
设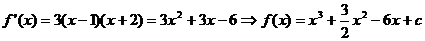 .
.
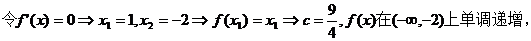 .
.
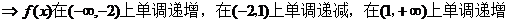 .
.
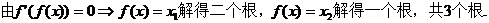
所以选A
第Ⅱ卷(非选择题 共100分)
二.填空题:本大题共5小题,每小题5分,共25分。把答案填在答题卡的相应位置。
(11)若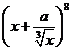 的展开式中
的展开式中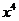 的系数为7,则实数
的系数为7,则实数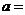 ___
___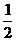 ___。
___。
【答案】 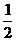
【解析】 通项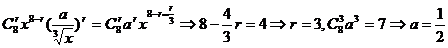
所以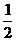
(12)设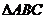 的内角
的内角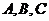 所对边的长分别为
所对边的长分别为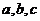 。若
。若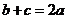 ,则
,则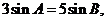 则角
则角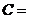 __
__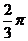 ___.
___.
【答案】 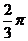
【解析】 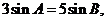
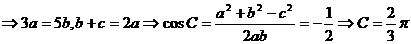
所以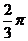
(13)已知直线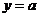 交抛物线
交抛物线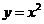 于
于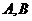 两点。若该抛物线上存在点
两点。若该抛物线上存在点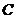 ,使得
,使得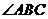 为直角,则
为直角,则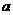 的取值范围为___
的取值范围为___ 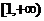 _____。
_____。
【答案】 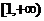
【解析】 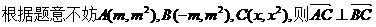
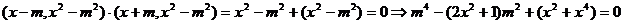

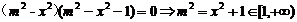 .所以
.所以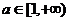
(14)如图,互不-相同的点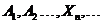 和
和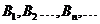 分别在角O的两条边上,所有
分别在角O的两条边上,所有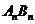 相互平行,且所有梯形
相互平行,且所有梯形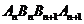 的面积均相等。设
的面积均相等。设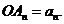 若
若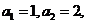 则数列
则数列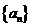 的通项公式是_____
的通项公式是_____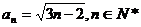 ____。
____。
【答案】 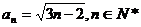
【解析】 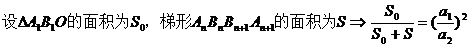 .
.
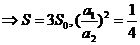
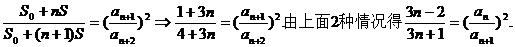
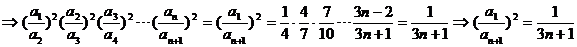
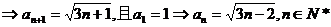
(15)如图,正方体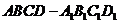 的棱长为1,P为BC的中点,Q为线段
的棱长为1,P为BC的中点,Q为线段 上的动点,过点A,P,Q的平面截该正方体所得的截面记为S。则下列命题正确的是__①②③⑤___(写出所有正确命题的编号)。
上的动点,过点A,P,Q的平面截该正方体所得的截面记为S。则下列命题正确的是__①②③⑤___(写出所有正确命题的编号)。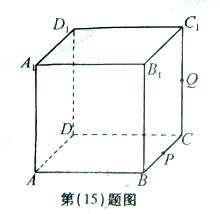
①当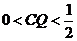 时,S为四边形
时,S为四边形
②当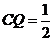 时,S为等腰梯形
时,S为等腰梯形
③当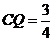 时,S与
时,S与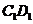 的交点R满足
的交点R满足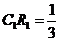
④当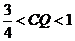 时,S为六边形
时,S为六边形
⑤当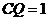 时,S的面积为
时,S的面积为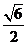
【答案】 ①②③⑤
【解析】 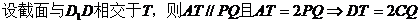 .
.
对①,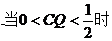 ,则
,则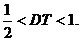 所以截面S为四边形,且S为梯形.所以为真.
所以截面S为四边形,且S为梯形.所以为真.
对②, 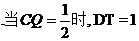
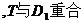 ,截面S为四边形
,截面S为四边形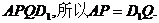 截面S为等腰梯形. 所以为真.
截面S为等腰梯形. 所以为真.
对③, 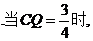
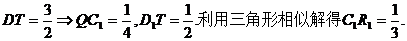 所以为真.
所以为真.
对④, 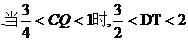 .截面S与线段
.截面S与线段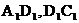 相交,所以四边形S为五边形.所以为假.
相交,所以四边形S为五边形.所以为假.
对⑤, 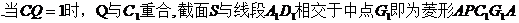 .对角线长度分别为
.对角线长度分别为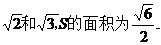 所以为真.
所以为真.
综上,选①②③⑤
三.解答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。解答写在答题卡上的指定区域内。
(16)(本小题满分12分)
已知函数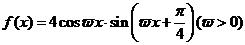 的最小正周期为
的最小正周期为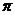 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)讨论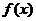 在区间
在区间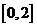 上的单调性。
上的单调性。
【答案】 (Ⅰ) 1
(Ⅱ) 
【解析】 (Ⅰ)
 .所以
.所以
(Ⅱ) 

所以
(17)(本小题满分12分)
设函数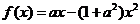 ,其中
,其中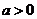 ,区间
,区间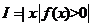
(Ⅰ)求的长度(注:区间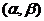 的长度定义为
的长度定义为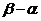 );
);
(Ⅱ)给定常数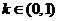 ,当时,求
,当时,求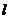 长度的最小值。
长度的最小值。
【答案】 (Ⅰ) 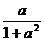 .
.
(Ⅱ) 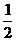
【解析】 (Ⅰ) .所以区间长度为
.所以区间长度为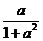 .
.
(Ⅱ) 若
 .
. .
.
(18)(本小题满分12分)
设椭圆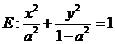 的焦点在
的焦点在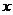 轴上
轴上
(Ⅰ)若椭圆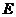 的焦距为1,求椭圆
的焦距为1,求椭圆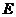 的方程;
的方程;
(Ⅱ)设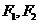 分别是椭圆的左、右焦点,
分别是椭圆的左、右焦点,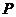 为椭圆
为椭圆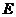 上的第一象限内的点,直线
上的第一象限内的点,直线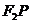 交
交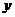 轴与点
轴与点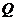 ,并且
,并且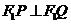 ,证明:当
,证明:当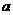 变化时,点
变化时,点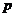 在某定直线上。
在某定直线上。
【答案】 (Ⅰ)  .
.
(Ⅱ) 
【解析】 (Ⅰ)
 .
.
(Ⅱ)  .
.
由 .
.
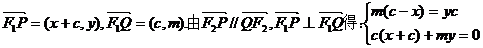
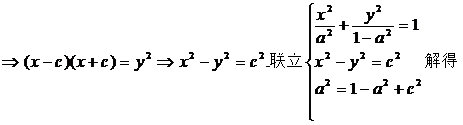
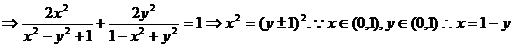
所以动点P过定直线 .
.
(19)(本小题满分13分)
如图,圆锥顶点为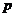 。底面圆心为
。底面圆心为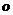 ,其母线与底面所成的角为22.5°。
,其母线与底面所成的角为22.5°。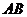 和
和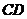 是底面圆
是底面圆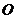 上的两条平行的弦,轴
上的两条平行的弦,轴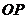 与平面
与平面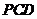 所成的角为60°,
所成的角为60°,
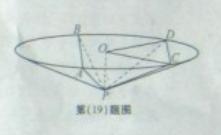
(Ⅰ)证明:平面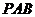 与平面
与平面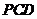 的交线平行于底面;
的交线平行于底面;
(Ⅱ)求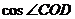 。
。
【答案】 (Ⅰ) 见下.
(Ⅱ) 
【解析】 (Ⅰ) 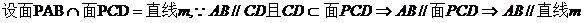
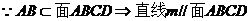 .
.
所以, .(证毕)
.(证毕)
(Ⅱ) 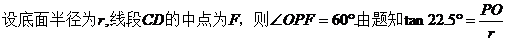 .
.
 .
.

 .(完)
.(完)
(20)(本小题满分13分)
设函数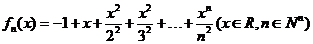 ,证明:
,证明:
(Ⅰ)对每个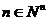 ,存在唯一的
,存在唯一的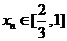 ,满足
,满足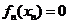 ;
;
(Ⅱ)对任意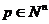 ,由(Ⅰ)中
,由(Ⅰ)中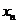 构成的数列
构成的数列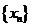 满足
满足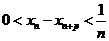 。
。
【答案】 (Ⅰ) 见下. (Ⅱ)见下.
【解析】 (Ⅰ) 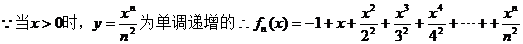 是x的单调递增函数,也是n的单调递增函数.
是x的单调递增函数,也是n的单调递增函数.  .
.

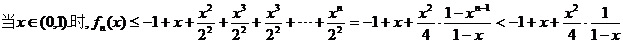

综上,对每个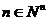 ,存在唯一的
,存在唯一的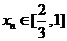 ,满足
,满足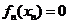 ;(证毕)
;(证毕)
(Ⅱ) 由题知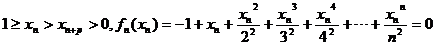
 上式相减:
上式相减:

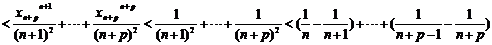

(21)(本小题满分13分)
某高校数学系计划在周六和周日各举行一次主题不同的心理测试活动,分别由李老师和张老师负责,已知该系共有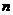 位学生,每次活动均需该系
位学生,每次活动均需该系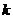 位学生参加(
位学生参加(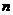 和
和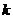 都是固定的正整数)。假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系
都是固定的正整数)。假设李老师和张老师分别将各自活动通知的信息独立、随机地发给该系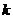 位学生,且所发信息都能收到。记该系收到李老师或张老师所发活动通知信息的学生人数为
位学生,且所发信息都能收到。记该系收到李老师或张老师所发活动通知信息的学生人数为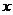
(Ⅰ)求该系学生甲收到李老师或张老师所发活动通知信息的概率;
(Ⅱ)求使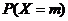 取得最大值的整数
取得最大值的整数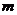 。
。
【答案】 (Ⅰ) 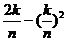 .
.
(Ⅱ) 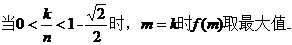

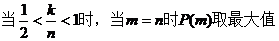
【解析】 (Ⅰ)  .
.
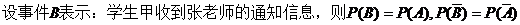 .
.
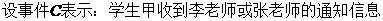 .
.
则 .
.
所以, .
.
(Ⅱ)  ,
,

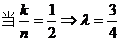 .
.
 ;
;
讨论如下:
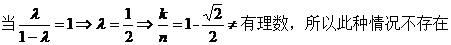 .
.
 .
.
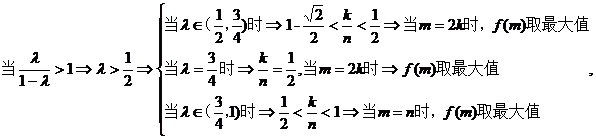 .
.