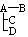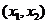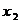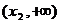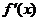(单词翻译:单击)
第I卷(选择题 共50分)
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)i是虚数单位,若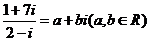 ,则乘积
,则乘积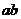 的值是
的值是
(A)-15 (B)-3 (C)3 (D)15
[解析] 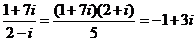 ,∴
,∴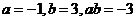 ,选B。
,选B。
(2)若集合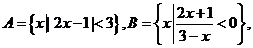 则A∩B是
则A∩B是
(A) 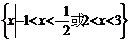 (B)
(B) 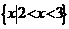 (C)
(C) 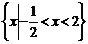 (D)
(D) 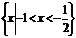
[解析]集合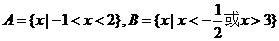 ,∴
,∴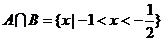 选D
选D
(3)下列曲线中离心率为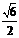 的是
的是
(A)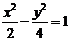 (B)
(B)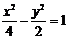 (C)
(C)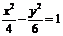 (D)
(D)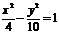
[解析]由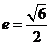 得
得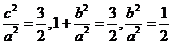 ,选B
,选B
(4)下列选项中,p是q的必要不充分条件的是
(A)p: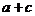 >b+d , q:
>b+d , q: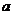 >b且c>d (B)p:a>1,b>1 q:
>b且c>d (B)p:a>1,b>1 q: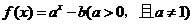 的图像不过第二象限(C)p: x=1, q:
的图像不过第二象限(C)p: x=1, q: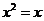 (D)p:a>1, q:
(D)p:a>1, q: 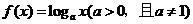 在
在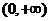 上为增函数
上为增函数
[解析]:由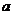 >b且c>d
>b且c>d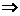
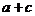 >b+d,而由
>b+d,而由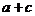 >b+d
>b+d 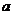 >b且c>d,可举反例。选A
>b且c>d,可举反例。选A
(5)已知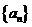 为等差数列,
为等差数列,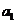 +
+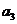 +
+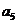 =105,
=105,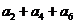 =99,以
=99,以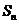 表示
表示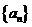 的前
的前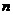 项和,则使得
项和,则使得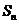 达到最大值的
达到最大值的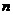 是
是
(A)21 (B)20 (C)19 (D) 18
[解析]:由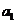 +
+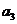 +
+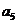 =105得
=105得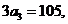 即
即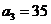 ,由
,由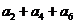 =99得
=99得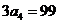 即
即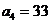 ,∴
,∴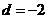 ,
,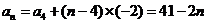 ,由
,由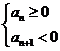 得
得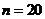 ,选B
,选B
(6)设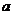 <b,函数
<b,函数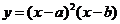 的图像可能是
的图像可能是
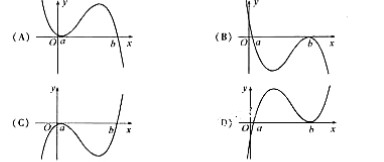
[解析]: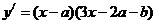 ,由
,由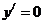 得
得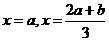 ,∴当
,∴当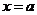 时,
时,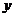 取极大值0,当
取极大值0,当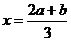 时
时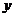 取极小值且极小值为负。故选C。或当
取极小值且极小值为负。故选C。或当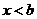 时
时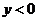 ,当
,当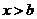 时,
时,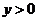 选C
选C
(7)若不等式组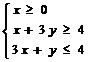 所表示的平面区域被直线
所表示的平面区域被直线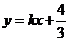 分为面积相等的两部分,则
分为面积相等的两部分,则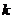 的值是
的值是
(A)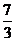 (B)
(B) 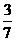 (C)
(C)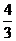 (D)
(D) 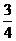
[解析]:不等式表示的平面区域如图所示阴影部分△ABC
由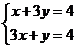 得A(1,1),又B(0,4),C(0,
得A(1,1),又B(0,4),C(0,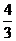 )
)
∴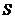 △ABC=
△ABC=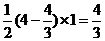 ,设
,设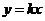 与
与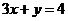 的
的
交点为D,则由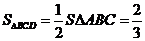 知
知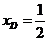 ,∴
,∴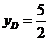
∴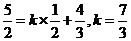 选A。
选A。
(8)已知函数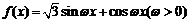 ,
,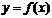 的图像与直线
的图像与直线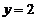 的两个相邻交点的距离等于
的两个相邻交点的距离等于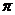 ,则
,则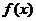 的单调递增区间是
的单调递增区间是
(A)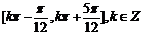 (B)
(B)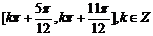 (C)
(C)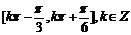 (D)
(D)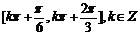
[解析]: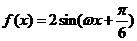 ,由题设
,由题设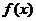 的周期为
的周期为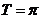 ,∴
,∴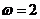 ,
,
由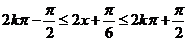 得,
得,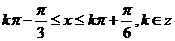 ,故选C
,故选C
(9)已知函数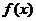 在R上满足
在R上满足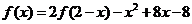 ,则曲线
,则曲线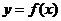 在点
在点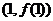 处的切线方程是
处的切线方程是
(A)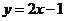 (B)
(B)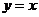 (C)
(C)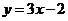 (D)
(D)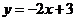
[解析]:由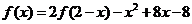 得
得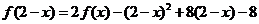 ,
,
即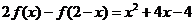 ,∴
,∴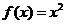 ∴
∴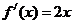 ,
,
∴切线方程为
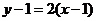 ,即
,即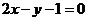 选A
选A
(10)考察正方体6个面的中心,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,则所得的两条直线相互平行但不重合的概率等于
(A)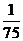 (B)
(B) 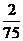 (C)
(C)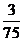 (D)
(D)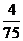
[解析] 如图,甲从这6个点中任意选两个点连成直线,乙也从这6个点中任意选两个点连成直线,共有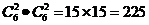 种不同取法,其中所得的两条直线相互平行但不重合有
种不同取法,其中所得的两条直线相互平行但不重合有
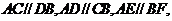
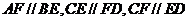

 共12对,所以所求概率为
共12对,所以所求概率为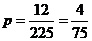 ,选D
,选D
第Ⅱ卷(非选择题 共100分)
考生注意事项: 请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效.
二.填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。
(11)若随机变量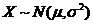 ,则
,则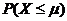 =________.
=________.
[解析] 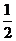
(12)以直角坐标系的原点为极点,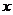 轴的正半轴为极轴,并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为
轴的正半轴为极轴,并在两种坐标系中取相同的长度单位。已知直线的极坐标方程为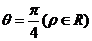 ,它与曲线
,它与曲线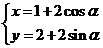 (
(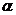 为参数)相交于两点A和B,则|AB|=_______.
为参数)相交于两点A和B,则|AB|=_______.
[解析] 直线的普通方程为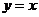 ,曲线的普通方程
,曲线的普通方程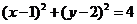
∴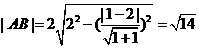
(13) 程序框图(即算法流程图)如图所示,其输出结果是_______.
[解析] 由程序框图知,循环体被执行后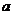 的值依次为3、7、15、31、
的值依次为3、7、15、31、
63、127,故输出的结果是127。
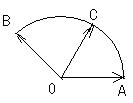
(14)给定两个长度为1的平面向量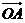 和
和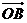 ,它们的夹角为
,它们的夹角为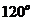 .如图所示,点C在以O为圆心的圆弧
.如图所示,点C在以O为圆心的圆弧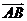 上变动.若
上变动.若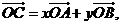 其中
其中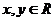 ,则
,则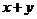 的最大值是________.
的最大值是________.
[解析]设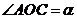
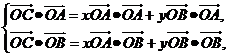 ,即
,即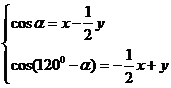
∴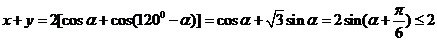
(15)对于四面体ABCD,下列命题正确的是_________
(写出所有正确命题的编号)。

1相对棱AB与CD所在的直线异面;
2由顶点A作四面体的高,其垂足是 BCD的三条高线的交点;
BCD的三条高线的交点;
3若分别作 ABC和
ABC和 ABD的边AB上的高,则这两条高所在直线异面;
ABD的边AB上的高,则这两条高所在直线异面;
4分别作三组相对棱中点的连线,所得的三条线段相交于一点;
5最长棱必有某个端点,由它引出的另两条棱的长度之和大于最长棱。
[解析]①④⑤
三.解答题;本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.解答写在答题卡上的答题区域内.
(16)在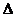 ABC中,
ABC中,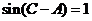 , sinB=
, sinB=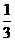 .
.
(I)求sinA的值;
(II)设AC=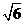 ,求
,求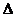 ABC的面积.
ABC的面积.
本小题主要考查三角恒等变换、正弦定理、解三角形等有关知识,考查运算求解能力。本小题满分12分
解:(Ⅰ)由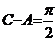 ,且
,且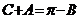 ,∴
,∴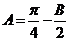 ,∴
,∴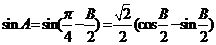 ,
,
∴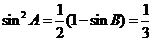 ,又
,又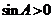 ,∴
,∴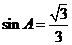
(Ⅱ)如图,由正弦定理得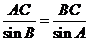
∴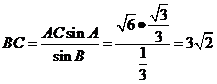 ,又
,又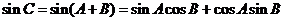
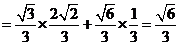
∴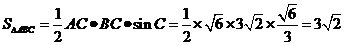


(17)(本小题满分12分)
某地有A、B、C、D四人先后感染了甲型H1N1流感,其中只有A到过疫区.B肯定是受A感染的.对于C,因为难以断定他是受A还是受B感染的,于是假定他受A和受B感染的概率都是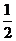 .同样也假定D受A、B和C感染的概率都是
.同样也假定D受A、B和C感染的概率都是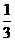 .在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
.在这种假定之下,B、C、D中直接受A感染的人数X就是一个随机变量.写出X的分布列(不要求写出计算过程),并求X的均值(即数学期望).
本小题主要考查古典概型及其概率计算,考查取有限个值的离散型随机变量及其分布列和均值的概念,通过设置密切贴近现实生活的情境,考查概率思想的应用意识和创新意识。体现数学的科学价值。本小题满分12分。
解:随机变量X的分布列是
X | 1 | 2 | 3 |
P |
|
|
|
X的均值为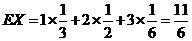
附:X的分布列的一种求法
共有如下6种不同的可能情形,每种情形发生的概率都是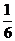 :
:
① | ② | ③ | ④ | ⑤ | ⑥ |
A—B—C—D | A—B—C └D | A—B—C └D | A—B—D └C | A—C—D └B |
|
在情形①和②之下,A直接感染了一个人;在情形③、④、⑤之下,A直接感染了两个人;在情形⑥之下,A直接感染了三个人。
(18)(本小题满分13分)
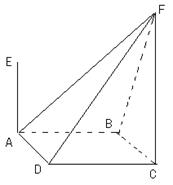
如图,四棱锥F-ABCD的底面ABCD是菱形,其对角线AC=2,BD=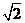 ,AE、CF都与平面ABCD垂直,AE=1,CF=2.
,AE、CF都与平面ABCD垂直,AE=1,CF=2.
(I)求二面角B-AF-D的大小;
(II)求四棱锥E-ABCD与四棱锥F-ABCD公共部分的体积.
本小题主要考查直线与直线、直线与平面、平面与平面的位置关系、相交平面所成二面角以及空间几何体的体积计算等知识,考查空间想象能力和推理论证能力、利用综合法或向量法解决立体几何问题的能力。本小题满分13分。
解:(I)(综合法)连接AC、BD交于菱形的中心O,过O作OG AF,
AF,
G为垂足。连接BG、DG。由BD AC,BD
AC,BD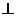 CF得BD
CF得BD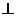 平面ACF,故BD
平面ACF,故BD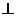 AF。
AF。
于是AF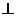 平面BGD,所以BG
平面BGD,所以BG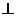 AF,DG
AF,DG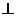 AF,
AF,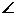 BGD为二面角B-AF-D 的平面角。
BGD为二面角B-AF-D 的平面角。
由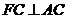 ,
, 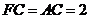 ,得
,得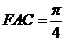 ,
,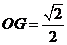


由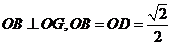 ,得
,得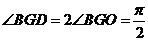
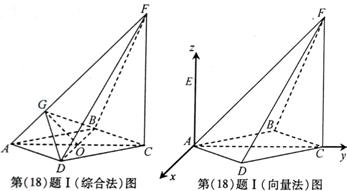
(向量法)以A为坐标原点,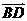 、
、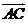 、
、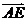 方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系(如图)
方向分别为x轴、y轴、z轴的正方向建立空间直角坐标系(如图)
设平面ABF的法向量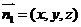 ,则由
,则由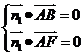 得
得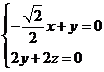
令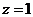 ,得
,得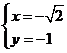 ,
,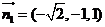
同理,可求得平面ADF的法向量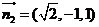 。
。

由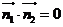 知,平面ABF与平面ADF垂直,
知,平面ABF与平面ADF垂直,
二面角B-AF-D的大小等于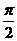 。
。
(II)连EB、EC、ED,设直线AF与直线CE相交于点H,则四棱锥E-ABCD与四棱锥F-ABCD的公共部分为四棱锥H-ABCD。
过H作HP⊥平面ABCD,P为垂足。
因为EA⊥平面ABCD,FC⊥平面ABCD,,所以平面ACFE⊥平面ABCD,从而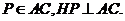
由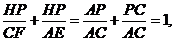 得
得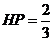 。
。
又因为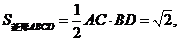


故四棱锥H-ABCD的体积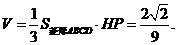
(19)(本小题满分12分)
已知函数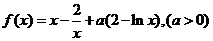 ,讨论
,讨论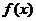 的单调性.
的单调性.
本小题主要考查函数的定义域、利用导数等知识研究函数的单调性,考查分类讨论的思想方法和运算求解的能力。本小题满分12分。
解: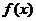 的定义域是(0,+
的定义域是(0,+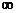 ),
),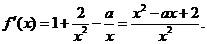
设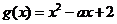 ,二次方程
,二次方程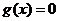 的判别式
的判别式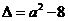 .
.
① 当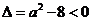 ,即
,即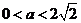 时,对一切
时,对一切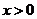 都有
都有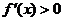 ,此时
,此时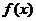 在
在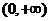 上是增函数。
上是增函数。
② 当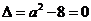 ,即
,即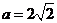 时,仅对
时,仅对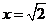 有
有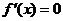 ,对其余的
,对其余的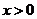 都有
都有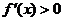 ,此时
,此时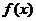 在
在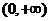 上也是增函数。
上也是增函数。

③ 当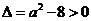 ,即
,即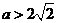 时,
时,
方程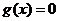 有两个不同的实根
有两个不同的实根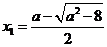 ,
,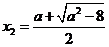 ,
,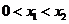 .
.
|
|
|
|
|
|
| + | 0 | _ | 0 | + |
| 单调递增 | 极大 | 单调递减 | 极小 | 单调递增 |
此时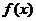 在
在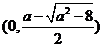 上单调递增, 在
上单调递增, 在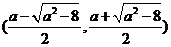 是上单调递减, 在
是上单调递减, 在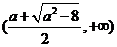 上单调递增.
上单调递增.
(20)(本小题满分13分)
点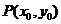 在椭圆
在椭圆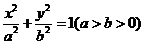 上,
上,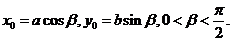 直线
直线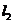 与直线
与直线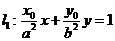 垂直,O为坐标原点,直线OP的倾斜角为
垂直,O为坐标原点,直线OP的倾斜角为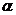 ,直线
,直线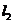 的倾斜角为
的倾斜角为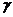 .
.
(I)证明: 点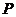 是椭圆
是椭圆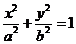 与直线
与直线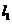 的唯一交点;
的唯一交点;

(II)证明: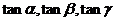 构成等比数列.
构成等比数列.
解:本小题主要考查直线和椭圆的标准方程和参数方程,直线和曲线的几何性质,等比数列等基础知识。考查综合运用知识分析问题、解决问题的能力。本小题满分13分。
解:(I)(方法一)由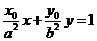 得
得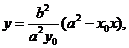 代入椭圆
代入椭圆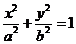 ,
,
得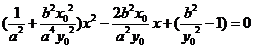 .
.
将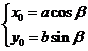 代入上式,得
代入上式,得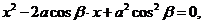 从而
从而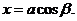
因此,方程组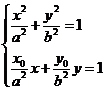 有唯一解
有唯一解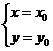 ,即直线
,即直线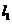 与椭圆有唯一交点P.
与椭圆有唯一交点P.

(方法二)显然P是椭圆与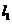 的交点,若Q
的交点,若Q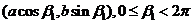 是椭圆与
是椭圆与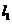 的交点,代入
的交点,代入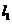 的方程
的方程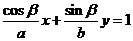 ,得
,得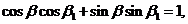
即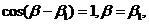 故P与Q重合。
故P与Q重合。
(方法三)在第一象限内,由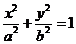 可得
可得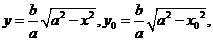
椭圆在点P处的切线斜率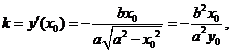
切线方程为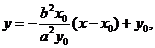 即
即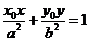 。
。
因此,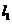 就是椭圆在点P处的切线。
就是椭圆在点P处的切线。
根据椭圆切线的性质,P是椭圆与直线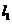 的唯一交点。
的唯一交点。
(II)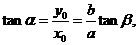
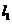 的斜率为
的斜率为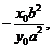
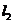 的斜率为
的斜率为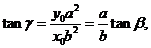
由此得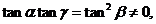
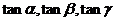 构成等比数列。
构成等比数列。
(21)(本小题满分13分)
首项为正数的数列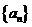 满足
满足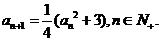


(I)证明:若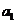 为奇数,则对一切
为奇数,则对一切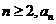 都是奇数;
都是奇数;
(II)若对一切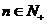 都有
都有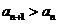 ,求
,求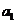 的取值范围.
的取值范围.
解:本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野。本小题满分13分。
解:(I)已知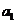 是奇数,假设
是奇数,假设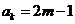 是奇数,其中
是奇数,其中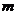 为正整数,
为正整数,
则由递推关系得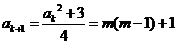 是奇数。
是奇数。

根据数学归纳法,对任何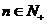 ,
,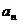 都是奇数。
都是奇数。
(II)(方法一)由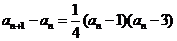 知,
知,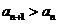 当且仅当
当且仅当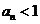 或
或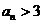 。
。
另一方面,若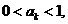 则
则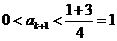 ;若
;若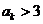 ,则
,则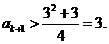
根据数学归纳法,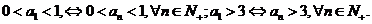
综合所述,对一切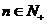 都有
都有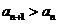 的充要条件是
的充要条件是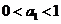 或
或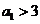 。
。
(方法二)由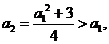 得
得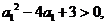 于是
于是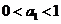 或
或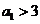 。
。
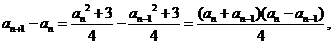


因为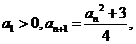 所以所有的
所以所有的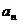 均大于0,因此
均大于0,因此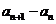 与
与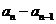 同号。
同号。
根据数学归纳法,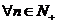 ,
,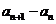 与
与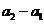 同号。
同号。

因此,对一切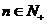 都有
都有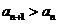 的充要条件是
的充要条件是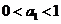 或
或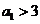 。
。