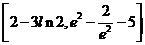(单词翻译:单击)
第I卷(选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. i是虚数单位,i(1+i)等于
A.1+i B. -1-i C.1-i D. -1+i
2. 若集合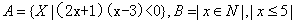 ,则
,则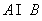 是
是
A.{1,2,3} B. {1,2}
C. {4,5} D. {1,2,3,4,5}
3.不等式组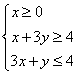 所表示的平面区域的面积等于
所表示的平面区域的面积等于
A. 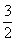 B.
B. 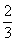
C. 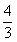 D.
D. 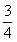
4.“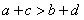 ”是“
”是“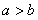 且
且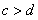 ”的
”的
A. 必要不充分条件 B. 充分不必要条件
C. 充分必要条件 D. 既不充分也不必要条件
5.已知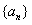 为等差数列,
为等差数列,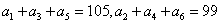 ,则
,则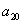 等于
等于
A. -1 B. 1 C. 3 D.7
6.下列曲线中离心率为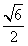 的是
的是

A.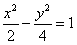 B.
B.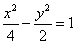 C.
C.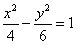 D.
D. 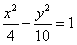
7. 直线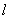 过点(-1,2)且与直线垂直,则
过点(-1,2)且与直线垂直,则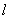 的方程是
的方程是
A.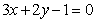 B.
B.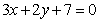
C. 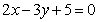 D.
D. 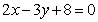
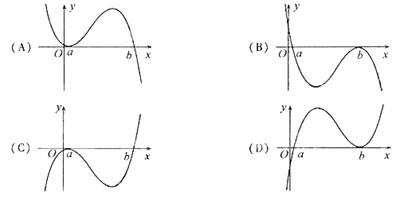
8.设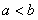 ,函数
,函数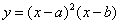 的图像可能是
的图像可能是
9.设函数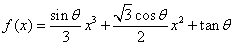 ,其中
,其中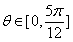 ,则导数
,则导数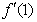 的取值范围是
的取值范围是
A. 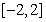 B.
B. 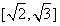 C.
C.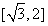 D.
D. 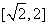
10.考察正方体6个面的中心,从中任意选3个点连成三角形,再把剩下的3个点也连成三角形,则所得的两个三角形全等的概率等于
A.1 B.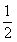 C.
C.  D. 0
D. 0
第II卷(非选择题 共100分)
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在答题卡的相应位置。
11.在空间直角坐标系中,已知点A(1,0,2),B(1,-3,1),点M在y轴上,且M到A与到B的距离相等,则M的坐标是________。
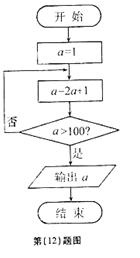
12.程序框图(即算法流程图)如图所示,其输入结果是_______。
13.从长度分别为2、3、4、5的四条线段中任意取出三条,则以这三条线段为边可以构成三角形的概率是________。
14.在平行四边形ABCD中,E和F分别是边CD和BC的中点,或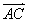 =
=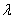
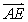 +
+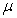
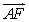 ,其中
,其中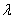 ,
,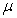
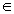 R ,则
R ,则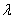 +
+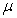 = _________。
= _________。

15.对于四面体ABCD,下列命题正确的是_________(写出所有正确命题的编号)。
○11相对棱AB与CD所在的直线是异面直线;
○22由顶点A作四面体的高,其垂足是 BCD的三条高线的交点;
BCD的三条高线的交点;
○33若分别作 ABC和
ABC和 ABD的边AB上的高,则这两条高的垂足重合;
ABD的边AB上的高,则这两条高的垂足重合;
○44任何三个面的面积之和都大于第四个面的面积;
○55分别作三组相对棱中点的连线,所得的三条线段相交于一点。
三.解答题;本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。解答写在答题卡上的指定区域内。
16.(本小题满分12分)
在 ABC中,C-A=
ABC中,C-A=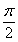 , sinB=
, sinB=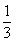 。
。
(I)求sinA的值;
(II)设AC=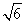 ,求
,求 ABC的面积。
ABC的面积。
17.(本小题满分12分)
某良种培育基地正在培育一种小麦新品种A,将其与原有的一个优良品种B进行对照试验,两种小麦各种植了25亩,所得亩产数据(单位:千克)如下:
品种A:357,359,367,368,375,388,392,399,400,405,414,
415,421,423,423,427,430,430,434,443,445,451,454
品种B:363,371,374,383,385,386,391,392,394,395,397
397,400,401,401,403,406,407,410,412,415,416,422,430
(Ⅰ)完成所附的茎叶图
(Ⅱ)用茎叶图处理现有的数据,有什么优点?
(Ⅲ)通过观察茎叶图,对品种A与B的亩产量及其稳定性进行比较,写出统计结论。
18.(本小题满分12分)
已知椭圆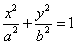 (a>b>0)的离心率为
(a>b>0)的离心率为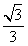 ,以原点为圆心。椭圆短半轴长半径的圆与直线y=x+2相切,
,以原点为圆心。椭圆短半轴长半径的圆与直线y=x+2相切,
(Ⅰ)求a与b;
(Ⅱ)设该椭圆的左,右焦点分别为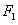 和
和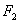 ,直线
,直线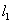 过
过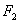 且与x轴垂直,动直线
且与x轴垂直,动直线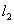 与y轴垂直,
与y轴垂直,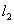 交
交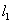 与点p..求线段P
与点p..求线段P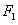 垂直平分线与
垂直平分线与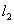 的交点M的轨迹方程,并指明曲线类型。
的交点M的轨迹方程,并指明曲线类型。
19.(本小题满分12分)
已知数列{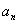 } 的前n项和
} 的前n项和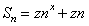 ,数列{
,数列{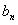 }的前n项和
}的前n项和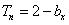
(Ⅰ)求数列{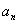 }与{
}与{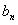 }的通项公式;
}的通项公式;
(Ⅱ)设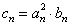 ,证明:当且仅当n≥3时,
,证明:当且仅当n≥3时,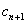 <
<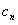
20.(本小题满分13分)
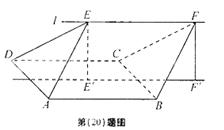
如图,ABCD的边长为2的正方形,直线l与平面ABCD平行,g和F式l上的两个不同点,且EA=ED,FB=FC, 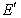 和
和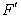 是平面ABCD内的两点,
是平面ABCD内的两点,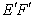 和
和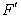
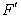 都与平面ABCD垂直,
都与平面ABCD垂直,
(Ⅰ)证明:直线 垂直且平分线段AD:
垂直且平分线段AD:
(Ⅱ)若∠EAD=∠EAB=60°,EF=2,求多面体ABCDEF的体积。
21.(本小题满分14分)
已知函数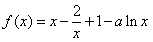 ,a>0,
,a>0,
(Ⅰ)讨论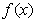 的单调性;
的单调性;
(Ⅱ)设a=3,求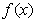 在区间{1,
在区间{1,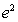 }上值域。期中e=2.71828…是自然对数的底数。
}上值域。期中e=2.71828…是自然对数的底数。
2009年普通高等学校招生全国统一考试(安徽卷)
数学(文科)参考答案
一、选择题
1- 10 D B C A B B A C D A
二、填空题
11.【解析】设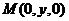 由
由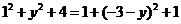 可得
可得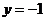 故
故 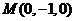
【答案】(0,-1,0)
12. 【解析】根据流程图可得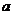 的取值依次为1、3、7、15、31、63……
的取值依次为1、3、7、15、31、63……

【答案】127
13. 【解析】依据四条边长可得满足条件的三角形有三种情况:
2、3、4或3、4、5或2、4、5,故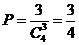 =0.75.
=0.75.
【答案】0.75
14.【解析】设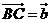 、
、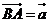 则
则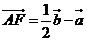 ,
,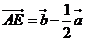 ,
,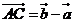
代入条件得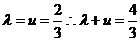
【答案】4/3
15. 【解析】由空间四面体棱,面关系可判断①④⑤正确,可举例说明②③错误.
【答案】①④⑤
三、解答题
16. 【思路】(1)依据三角函数恒等变形可得关于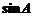 的式子,这之中要运用到倍角公式;
的式子,这之中要运用到倍角公式;
(2)应用正弦定理可得出边长,进而用面积公式可求出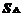 .
.
【解析】(1)∵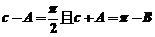 ∴
∴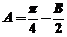
∴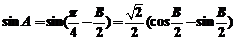
∴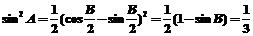
又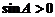 ∴
∴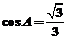
(2)如图,由正弦定理得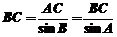 ∴
∴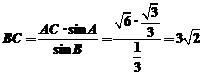
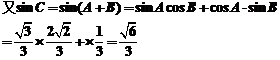
∴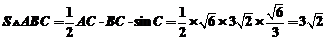 .
.
17. 【思路】由统计知识可求出A、B两种品种的小麦稳定性大小并画出茎叶图,用茎叶图处理数据,看其分布就比较明了。
【解析】(1)茎叶图如图所示
A | B | |
9 7 | 35 | |
8 7 | 36 | 3 |
5 | 37 | 1 4 |
8 | 38 | 3 5 6 |
9 2 | 39 | 1 2 4 457 7 |
5 0 | 40 | 0 1 1 3 6 7 |
5 4 2 | 41 | 0 2 5 6 |
7 3 3 1 | 42 | 2 |
4 0 0 | 43 | 0 |
5 5 3 | 44 | |
4 1 | 45 |
(2)用茎叶图处理现有的数据不仅可以看出数据的分布状况,而且可以看出每组中的具体数据.
(3)通过观察茎叶图,可以发现品种A的平均每亩产量为411.1千克,品种B的平均亩产量为397.8千克.由此可知,品种A的平均亩产量比品种B的平均亩产量高.但品种A的亩产量不够稳定,而品种B的亩产量比较集中D平均产量附近.
18. 【思路】(1)由椭圆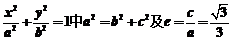 建立a、b等量关系,再根据直线与椭圆相切求出a、b.
建立a、b等量关系,再根据直线与椭圆相切求出a、b.
(2)依据几何关系转化为代数方程可求得,这之中的消参就很重要了。
【解析】(1)由于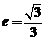 ∴
∴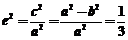 ∴
∴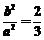 又
又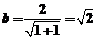 ∴b2=2,a2=3因此,
∴b2=2,a2=3因此,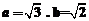 .
.
(2)由(1)知F1,F2两点分别为(-1,0),(1,0),由题意可设P(1,t).(t≠0).那么线段PF1中点为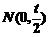 ,设M(x、y)是所求轨迹上的任意点.由于
,设M(x、y)是所求轨迹上的任意点.由于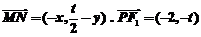 则
则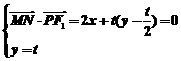 消去参数t得
消去参数t得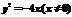
,其轨迹为抛物线(除原点)
19. 【思路】由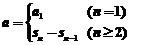 可求出
可求出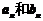 ,这是数列中求通项的常用方法之一,在求出
,这是数列中求通项的常用方法之一,在求出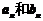 后,进而得到
后,进而得到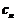 ,接下来用作差法来比较大小,这也是一常用方法。
,接下来用作差法来比较大小,这也是一常用方法。
【解析】(1)由于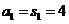
当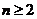 时,
时, 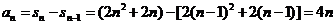
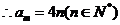
又当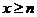 时
时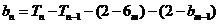
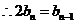
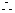 数列
数列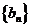 项与等比数列,其首项为1,公比为
项与等比数列,其首项为1,公比为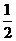
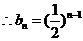
(2)由(1)知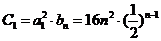
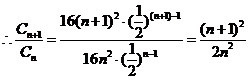
由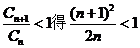 即
即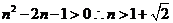 即
即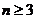
又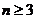 时
时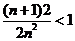 成立,即
成立,即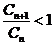 由于
由于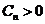 恒成立.
恒成立.
因此,当且仅当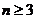 时,
时, 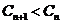
20. 【思路】根据空间线面关系可证线线垂直,由分割法可求得多面体体积,体现的是一种部分与整体的基本思想。
【解析】(1)由于EA=ED且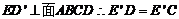
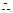 点E
点E 在线段AD的垂直平分线上,同理点F
在线段AD的垂直平分线上,同理点F 在线段BC的垂直平分线上.
在线段BC的垂直平分线上.
又ABCD是四方形
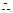 线段BC的垂直平分线也就是线段AD的垂直平分线
线段BC的垂直平分线也就是线段AD的垂直平分线
即点E F
F 都居线段AD的垂直平分线上.
都居线段AD的垂直平分线上.
所以,直线E F
F 垂直平分线段AD.
垂直平分线段AD.
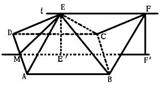 (2)连接EB、EC由题意知多面体ABCD可分割成正四棱锥E—ABCD和正四面体E—BCF两部分.设AD中点为M,在Rt△MEE
(2)连接EB、EC由题意知多面体ABCD可分割成正四棱锥E—ABCD和正四面体E—BCF两部分.设AD中点为M,在Rt△MEE 中,由于ME
中,由于ME =1,
=1, 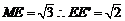 .
.
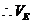 —ABCD
—ABCD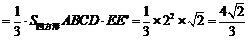
又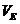 —BCF=VC-BEF=VC-BEA=VE-ABC
—BCF=VC-BEF=VC-BEA=VE-ABC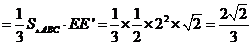
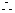 多面体ABCDEF的体积为VE—ABCD+VE—BCF=
多面体ABCDEF的体积为VE—ABCD+VE—BCF=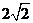
21. 【思路】由求导可判断得单调性,同时要注意对参数的讨论,即不能漏掉,也不能重复。第二问就根据第一问中所涉及到的单调性来求函数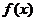 在
在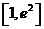 上的值域。
上的值域。
【解析】(1)由于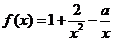
令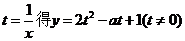
①当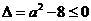 ,即
,即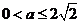 时,
时, 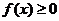 恒成立.
恒成立.
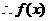 在(-∞,0)及(0,+∞)上都是增函数.
在(-∞,0)及(0,+∞)上都是增函数.
②当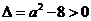 ,即
,即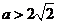 时
时
由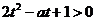 得
得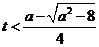 或
或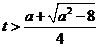
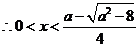 或
或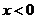 或
或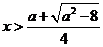
又由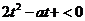 得
得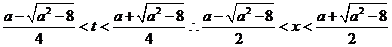
综上①当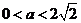 时,
时, 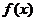 在
在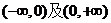 上都是增函数.
上都是增函数.
②当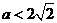 时,
时, 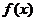 在
在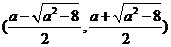 上是减函数,
上是减函数,
在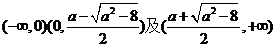 上都是增函数.
上都是增函数.
(2)当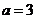 时,由(1)知
时,由(1)知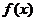 在
在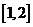 上是减函数.
上是减函数.
在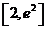 上是增函数.
上是增函数.
又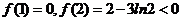
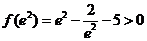
 函数
函数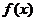 在
在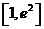 上的值域为
上的值域为