(单词翻译:单击)
选择题部分(共50分)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给也的四个选项中,只有一项是符合题
【答案】 A
【解析】: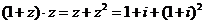
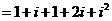
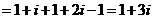 故选A
故选A
(3)若实数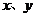 满足不等式组
满足不等式组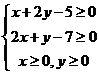 ,则
,则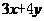 的最小值是
的最小值是
(A)13 (B)15 (C)20 (D)28
【答案】 A
【解析】:作出可行域,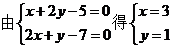 ,
, 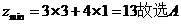
(4)若直线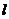 不平行于平面
不平行于平面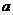 ,且
,且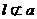 ,则
,则
(A) 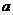 内的所有直线与
内的所有直线与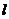 异面 (B)
异面 (B) 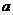 内不存在与
内不存在与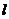 平行的直线
平行的直线
(C) 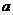 内存在唯一的直线与
内存在唯一的直线与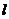 平行 (D)
平行 (D) 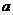 内的直线与
内的直线与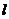 都相交
都相交
【答案】 B
【解析】:直线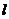 不平行于平面
不平行于平面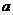 ,
,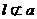 所以
所以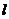 与
与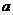 相交,故选B
相交,故选B
(5)在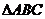 中,角
中,角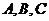 所对的
所对的 边分
边分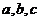 .若
.若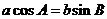 ,则
,则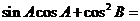
(A)- 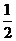 (B)
(B) 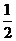
 (C) -1 (D) 1
(C) -1 (D) 1

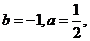
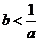 则
则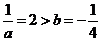
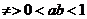 不必要条件,故选D
不必要条件,故选D
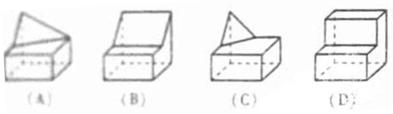
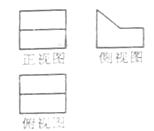
(7)几何体的三视图如图所示,则这个几何体的直观图可以是
【答案】 B
【解析】:A,C与正视图不符,D与俯视图不符,故选B
(8)从已有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概率 是
是
(A)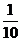 (B)
(B)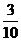 (C)
(C)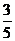 (D)
(D)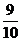
【答案】 D
【解析】:无白球的概率 是
是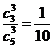 ,
,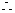 至少有1个白球的概率为
至少有1个白球的概率为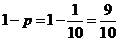 ,故选D
,故选D
(9)已知椭圆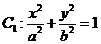 (a>b>0)与双曲线
(a>b>0)与双曲线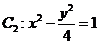 有公共的焦点
有公共的焦点 ,
,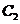 的一条渐近线与
的一条渐近线与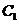
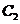 的长度为直径的圆相交于
的长度为直径的圆相交于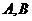 两点.若
两点.若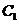 恰好将线段
恰好将线段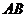 三等分,则
三等分,则
(A)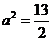 (B)
(B)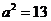 (C)
(C)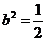 (D)
(D) 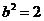

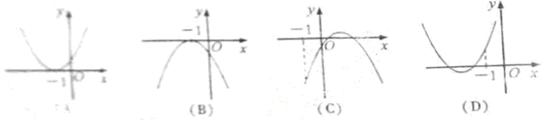
【答案】 D
【解析】: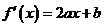 ,令
,令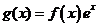 则
则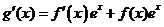
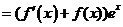
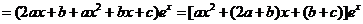 ,因为
,因为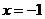 为函数
为函数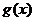 的一个极值点,所以
的一个极值点,所以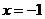 是
是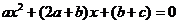 的一个根,即
的一个根,即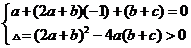
于是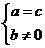 ,
,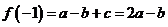 ,
,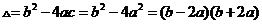
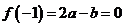 则
则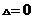 故A、B可能;对于D,
故A、B可能;对于D,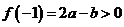 ,
,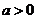 ,则
,则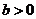 于是
于是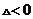 出现矛盾,不可能,故选D
出现矛盾,不可能,故选D
二、填空题:本大题共7小题,每小题4分,共28分。
(11)设函数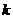
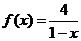 ,若
,若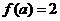 ,则实数
,则实数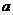 =____
=____
【答案】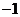
【解析】: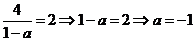
(12)若直线与直线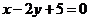 与直线
与直线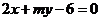 互相垂直,则实数
互相垂直,则实数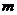 =_______
=_______
【答案】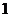
【解析】: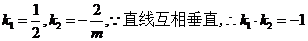 ,即
,即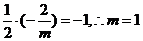

答案】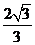
【解析】::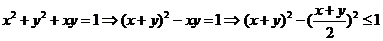
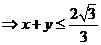
(17)若数列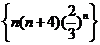 中的最大项是第
中的最大项是第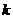 项,则
项,则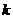 =_______。
=_______。
【答案】4
【解析】: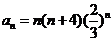 则
则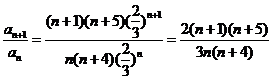
于是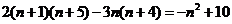 令
令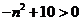 得
得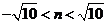 ,则
,则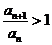 ,
, 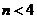 时递增,令
时递增,令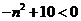 得
得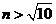 ,则
,则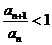 ,
,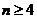 时递减,故
时递减,故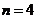 是最大项,即
是最大项,即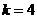
三、解答题,共72分。解答应写出文字说明、证明过程或演算步骤。
(18)(本题满分14分)已知函数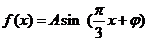 ,
,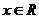 ,
,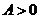 ,
,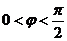 .
.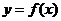 的部分图像,如图所示,
的部分图像,如图所示,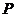 、
、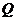 分别为该图像的最高点和最低点,点
分别为该图像的最高点和最低点,点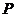 的坐标为
的坐标为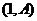 .
.
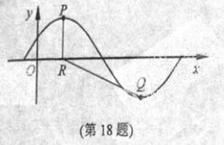
(Ⅰ)求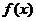 的最小正周期及
的最小正周期及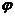 的值;(Ⅱ)若点
的值;(Ⅱ)若点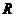 的坐标为
的坐标为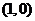 ,
,
19(本题满分14分)已知公差不为0的等差数列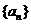 的首项
的首项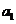 为
为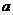 (
(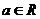 ),且
),且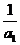 ,
,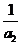 ,
,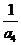 成等比数列(Ⅰ)求数列
成等比数列(Ⅰ)求数列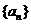 的通项公式(Ⅱ)对
的通项公式(Ⅱ)对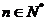 ,试比较
,试比较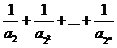 与
与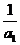 的大小.
的大小.
【解析】:(Ⅰ)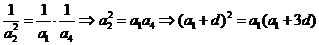
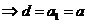
数列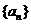 的通项公式
的通项公式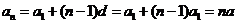
(Ⅱ)记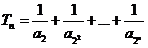 因为
因为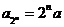 ,所以
,所以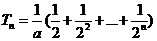
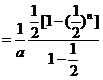
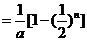 从而当
从而当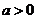 时,
时,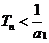 ;当
;当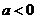 时,
时,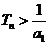
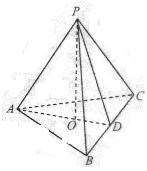
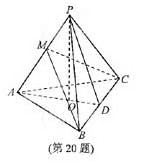
(20)(本题满分14分)如图,在三棱锥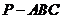 中,
中,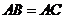 ,
,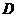 为
为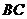 的
的 中点,
中点,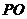 ⊥平面
⊥平面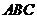 ,垂足
,垂足 落在线段
落在线段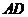 上.
上.
(Ⅰ)证明: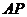 ⊥
⊥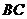 ;(Ⅱ)已知
;(Ⅱ)已知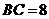 ,
,
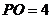 ,
,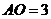 ,
,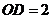 .求二面角
.求二面角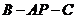 的大小.
的大小.
【解析】::(Ⅰ)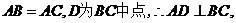

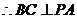
(Ⅱ)在平面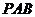 内作
内作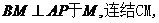
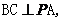 得
得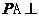 平面
平面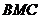 ,所以
,所以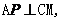
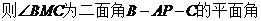 ,
,
在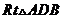 中,
中,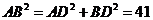 得
得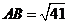
在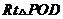 中,
中,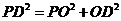 ,
,
在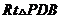 中,
中,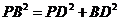
所以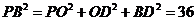 得
得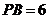 ,
,
在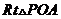 中,
中,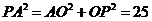 得
得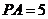
又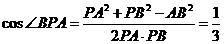 从而
从而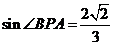 故
故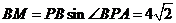
同理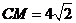 ,因为
,因为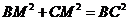 所以
所以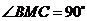 即二面角
即二面角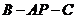 的大小为
的大小为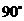
21(本题满分15分)设函数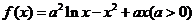 (Ⅰ)求
(Ⅰ)求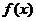 单调区间(Ⅱ)求所有实数
单调区间(Ⅱ)求所有实数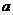 ,使
,使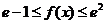 对
对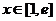 恒成立
恒成立
注: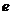 为自然对数的底数
为自然对数的底数
【解析】:(Ⅰ)因为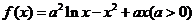 所以
所以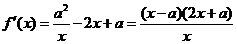 由于
由于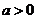
所以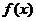 的增区间为
的增区间为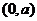 ,减区间为
,减区间为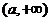 。
。
(Ⅱ)由题意得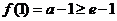 即
即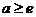 。由(Ⅰ)知
。由(Ⅰ)知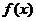 在
在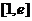 单调递增,要使
单调递增,要使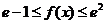
对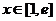 恒成立,只要
恒成立,只要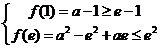 解得
解得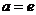
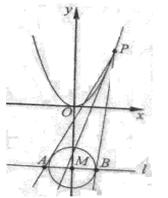
22.(本题满分15分)如图,设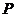 是抛物线
是抛物线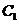 :
: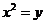 上动点。圆
上动点。圆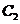 :
: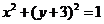 的圆心为点M,过点
的圆心为点M,过点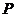 做圆
做圆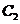 的两条切线,交直线
的两条切线,交直线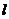 :
: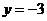 于
于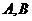 两点。
两点。
(Ⅰ)求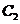 的圆心
的圆心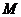 到抛物线
到抛物线 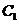 准线的距离。
准线的距离。
(Ⅱ)是否存在点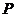 ,使线段
,使线段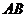 被抛物线
被抛物线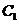 在点
在点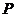 处得切线平分,若存在,求出点
处得切线平分,若存在,求出点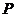 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
【解析】:(Ⅰ)由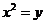 得准
得准 线方程为
线方程为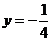 ,由
,由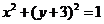 得
得 又
又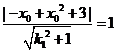 即
即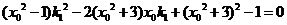
同理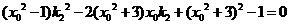 ,所以
,所以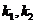 是方程
是方程
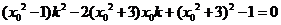 的两个不相等的根,从而
的两个不相等的根,从而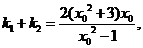
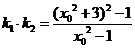 因为
因为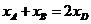 所以
所以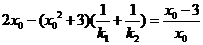 即
即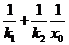
从而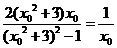 进而得
进而得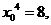
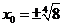 ,棕上所述,存在点
,棕上所述,存在点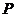 满足题意,
满足题意,
点 的坐标为
的坐标为