(单词翻译:单击)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设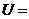
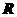 ,
,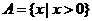 ,
,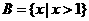 ,则
,则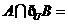 ( )
( )
A.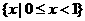 B.
B.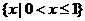 C.
C.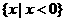 D.
D.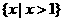
1. B 【命题意图】本小题主要考查了集合中的补集、交集的知识,在集合的运算考查对于集合理解和掌握的程度,当然也很好地考查了不等式的基本性质.
【解析】 对于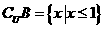 ,因此
,因此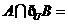
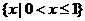 .
.
2.“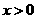 ”是“
”是“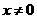 ”的( )
”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
2. A 【命题意图】本小题主要考查了命题的基本关系,题中的设问通过对不等关系的分析,考查了命题的概念和对于命题概念的理解程度.
【解析】对于“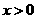 ”
”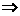 “
“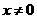 ”;反之不一定成立,因此“
”;反之不一定成立,因此“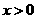 ”是“
”是“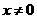 ”的充分而不必要条件.
”的充分而不必要条件.
3.设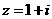 (
(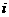 是虚数单位),则
是虚数单位),则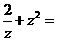 ( )
( )
A.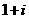 B.
B.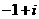 C.
C.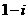 D.
D.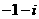
3.D 【命题意图】本小题主要考查了复数的运算和复数的概念,以复数的运算为载体,直接考查了对于复数概念和性质的理解程度.
【解析】对于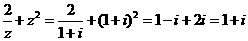
4.设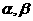 是两个不同的平面,
是两个不同的平面,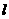 是一条直线,以下命题正确的是( )
是一条直线,以下命题正确的是( )
A.若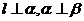 ,则
,则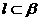 B.若
B.若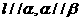 ,则
,则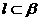
C.若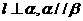 ,则
,则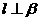 D.若
D.若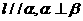 ,则
,则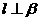
4.C 【命题意图】此题主要考查立体几何的线面、面面的位置关系,通过对平行和垂直的考查,充分调动了立体几何中的基本元素关系.
【解析】对于A、B、D均可能出现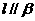 ,而对于C是正确的.
,而对于C是正确的.
5.已知向量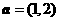 ,
,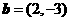 .若向量
.若向量 满足
满足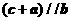 ,
,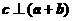 ,则
,则
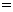 ( )
( )
A.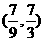 B.
B.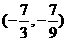 C.
C.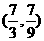 D.
D.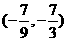
5.D 【命题意图】此题主要考查了平面向量的坐标运算,通过平面向量的平行和垂直关系的考查,很好地体现了平面向量的坐标运算在解决具体问题中的应用.
【解析】不妨设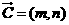 ,则
,则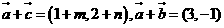 ,对于
,对于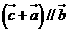 ,则有
,则有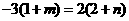 ;又
;又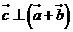 ,则有
,则有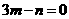 ,则有
,则有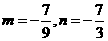
6.已知椭圆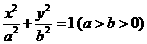 的左焦点为
的左焦点为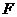 ,右顶点为
,右顶点为 ,点
,点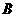 在椭圆上,且
在椭圆上,且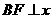 轴, 直线
轴, 直线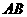 交
交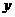 轴于点
轴于点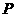 .若
.若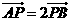 ,则椭圆的离心率是( )
,则椭圆的离心率是( )
A.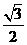 B.
B.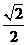 C.
C.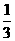 D.
D.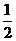
6.D 【命题意图】对于对解析几何中与平面向量结合的考查,既体现了几何与向量的交汇,也体现了数形结合的巧妙应用.
【解析】对于椭圆,因为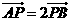 ,则
,则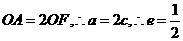


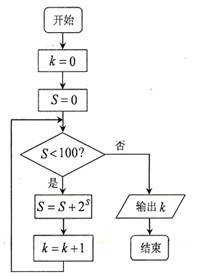
7.某程序框图如图所示,该程序运行后输出的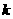 的值是( )
的值是( )
A.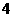 B.
B.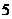
C.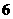 D.
D.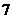
7.A 【命题意图】此题考查了程序语言的概念和基本的应用,通过对程序语言的考查,充分体现了数学程序语言中循环语言的关键.
【解析】对于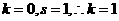 ,而对于
,而对于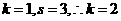 ,则
,则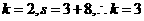 ,后面是
,后面是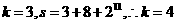 ,不符合条件时输出的
,不符合条件时输出的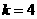 .
.
8.若函数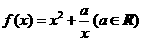 ,则下列结论正确的是( )
,则下列结论正确的是( )
A.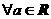 ,
,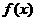 在
在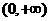 上是增函数
上是增函数
B.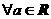 ,
,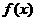 在
在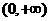 上是减函数
上是减函数
C.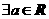 ,
,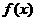 是偶函数
是偶函数
D.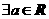 ,
,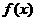 是奇函数
是奇函数
8.C 【命题意图】此题主要考查了全称量词与存在量词的概念和基础知识,通过对量词的考查结合函数的性质进行了交汇设问.
【解析】对于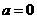 时有
时有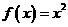 是一个偶函数
是一个偶函数
9.已知三角形的三边长分别为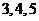 ,则它的边与半径为
,则它的边与半径为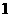 的圆的公共点个数最多为( )
的圆的公共点个数最多为( )
A.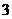 B.
B.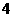 C.
C.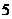 D.
D.
9.C 【命题意图】此题很好地考查了平面几何的知识,全面而不失灵活,考查的方法上面的要求平实而不失灵动,既有切线与圆的位置,也有圆的移动
【解析】对于半径为1的圆有一个位置是正好是三角形的内切圆,此时只有三个交点,对于圆的位置稍一右移或其他的变化,能实现4个交点的情况,但5个以上的交点不能实现.
10.已知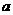 是实数,则函数
是实数,则函数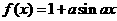 的图象不可能是( )
的图象不可能是( )

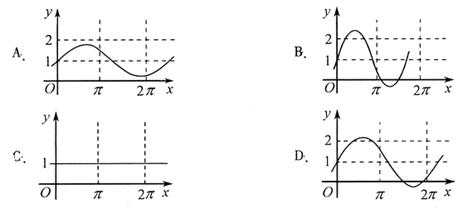
10.D 【命题意图】此题是一个考查三角函数图象的问题,但考查的知识点因含有参数而丰富,结合图形考查使得所考查的问题形象而富有深度.
【解析】对于振幅大于1时,三角函数的周期为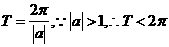 ,而D不符合要求,它的振幅大于1,但周期反而大于了
,而D不符合要求,它的振幅大于1,但周期反而大于了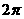 .
.
非选择题部分(共100分)
二、填空题:本大题共7小题,每小题4分,共28分。
11.设等比数列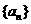 的公比
的公比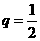 ,前
,前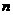 项和为
项和为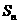 ,则
,则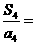 ____________.
____________. 

11.15 【命题意图】此题主要考查了数列中的等比数列的通项和求和公式,通过对数列知识点的考查充分体现了通项公式和前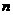 项和的知识联系.
项和的知识联系.
【解析】对于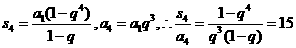
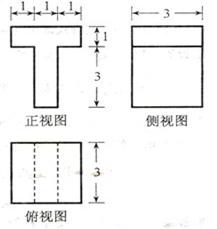
12.若某几何体的三视图(单位: )如图所示,则此几何体的体积是 ____________
)如图所示,则此几何体的体积是 ____________ 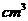 .
.
12. 18 【命题意图】此题主要是考查了几何体的三视图,通过三视图的考查充分体现了几何体直观的考查要求,与表面积和体积结合的考查方法.
【解析】该几何体是由二个长方体组成,下面体积为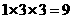 ,上面的长方体体积为
,上面的长方体体积为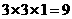 ,因此其几何体的体积为18
,因此其几何体的体积为18
13.若实数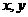 满足不等式组
满足不等式组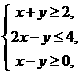 则
则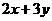 的最小值是 ____________.
的最小值是 ____________.
13. 4【命题意图】此题主要是考查了线性规划中的最值问题,此题的考查既体现了正确画线性区域的要求,也体现了线性目标函数最值求解的要求
【解析】通过画出其线性规划,可知直线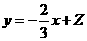 过点
过点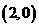 时,
时,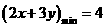
14.某个容量为 的样本的频率分布直方图如下,则在区间
的样本的频率分布直方图如下,则在区间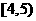 上的数据的频数为 ____________.
上的数据的频数为 ____________.

14. 30【命题意图】此题考查了频率分布直方图,通过设问既考查了设图能力,也考查了运用图表解决实际问题的水平和能力
【解析】对于在区间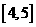 的频率/组距的数值为
的频率/组距的数值为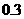 ,而总数为100,因此频数为30
,而总数为100,因此频数为30
15.某地区居民生活用电分为高峰和低谷两个时间段进行分时计价.该地区的电网销售电价表如下:
高峰时间段用电价格表 | 低谷时间段用电价格表 | ||
高峰月用电量 (单位:千瓦时) | 高峰电价 (单位:元/千瓦时) | 低谷月用电量 (单位:千瓦时) | 低谷电价 (单位:元/千瓦时) |
50及以下的部分 | 0.568 | 50及以下的部分 | 0.288 |
超过50至200的部分 | 0.598 | 超过50至200的部分 | 0.318 |
超过200的部分 | 0.668 | 超过200的部分 | 0.388 |
若某家庭5月份的高峰时间段用电量为 千瓦时,低谷时间段用电量为
千瓦时,低谷时间段用电量为 千瓦时,
千瓦时,
则按这种计费方式该家庭本月应付的电费为 元(用数字作答).
15. 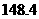 【命题意图】此题是一个实际应用性问题,通过对实际生活中的电费的计算,既考查了函数的概念,更侧重地考查了分段函数的应用
【命题意图】此题是一个实际应用性问题,通过对实际生活中的电费的计算,既考查了函数的概念,更侧重地考查了分段函数的应用
【解析】对于应付的电费应分二部分构成,高峰部分为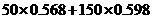 ;对于低峰部分为
;对于低峰部分为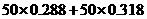 ,二部分之和为
,二部分之和为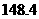

16.设等差数列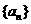 的前
的前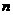 项和为
项和为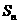 ,则
,则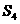 ,
,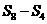 ,
,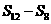 ,
,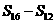 成等差数列.类比以上结论有:设等比数列
成等差数列.类比以上结论有:设等比数列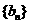 的前
的前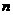 项积为
项积为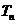 ,则
,则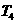 ,
, 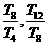 ,
,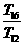 成等比数列.
成等比数列.
16. 【命题意图】此题是一个数列与类比推理结合的问题,既考查了数列中等差数列和等比数列的知识,也考查了通过已知条件进行类比推理的方法和能力

【解析】对于等比数列,通过类比,有等比数列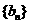 的前
的前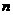 项积为
项积为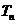 ,则
,则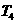 ,
,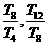 ,
,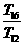 成等比数列.
成等比数列.
17.有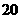 张卡片,每张卡片上分别标有两个连续的自然数
张卡片,每张卡片上分别标有两个连续的自然数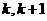 ,其中
,其中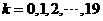 .从这
.从这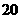 张卡片中任取一张,记事件“该卡片上两个数的各位数字之和(例如:若取到标有
张卡片中任取一张,记事件“该卡片上两个数的各位数字之和(例如:若取到标有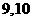 的卡片,则卡片上两个数的各位数字之和为
的卡片,则卡片上两个数的各位数字之和为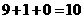 )不小于
)不小于 ”为
”为 ,则
,则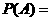 ____________.
____________.
17. 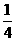 【命题意图】此题是一个排列组合问题,既考查了分析问题,解决问题的能力,更侧重于考查学生便举问题解决实际困难的能力和水平
【命题意图】此题是一个排列组合问题,既考查了分析问题,解决问题的能力,更侧重于考查学生便举问题解决实际困难的能力和水平
【解析】对于大于14的点数的情况通过列举可得有5种情况,即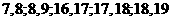 ,而基本事件有20种,因此
,而基本事件有20种,因此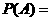
三、解答题:本大题共5小题,共72分。解答应写出文字说明、证明过程或演算步骤。
18.(本题满分14分)在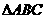 中,角
中,角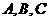 所对的边分别为
所对的边分别为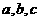 ,且满足
,且满足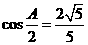 ,
,
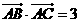 .
.
(I)求 的面积; (II)若
的面积; (II)若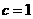 ,求
,求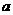 的值.
的值.
18.解析:(Ⅰ)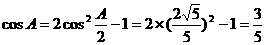

又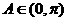 ,
,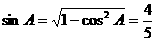 ,而
,而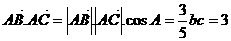 ,所以
,所以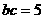 ,所以
,所以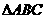 的面积为:
的面积为: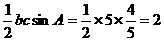
(Ⅱ)由(Ⅰ)知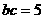 ,而
,而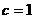 ,所以
,所以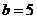
所以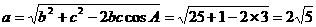
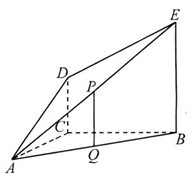
19.(本题满分14分)如图,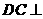 平面
平面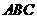 ,
,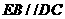 ,
,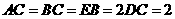 ,
,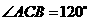 ,
,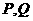 分别为
分别为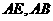 的中点.(I)证明:
的中点.(I)证明: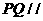 平面
平面 ;(II)求
;(II)求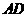 与平面
与平面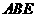 所成角的正弦值.
所成角的正弦值.
19.(Ⅰ)证明:连接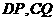 , 在
, 在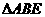 中,
中,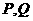 分别是
分别是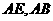 的中点,所以
的中点,所以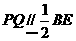 , 又
, 又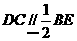 ,所以
,所以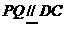 ,又
,又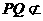 平面ACD ,DC
平面ACD ,DC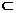 平面ACD, 所以
平面ACD, 所以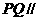 平面ACD
平面ACD
(Ⅱ)在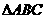 中,
中,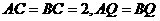 ,所以
,所以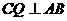 而DC
而DC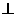 平面ABC,
平面ABC,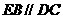 ,所以
,所以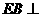 平面ABC
平面ABC
而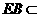 平面ABE, 所以平面ABE
平面ABE, 所以平面ABE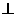 平面ABC, 所以
平面ABC, 所以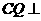 平面ABE,由(Ⅰ)知四边形DCQP是平行四边形,所以
平面ABE,由(Ⅰ)知四边形DCQP是平行四边形,所以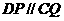 所以
所以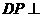 平面ABE, 所以直线AD在平面ABE内的射影是AP,所以直线AD与平面ABE所成角是
平面ABE, 所以直线AD在平面ABE内的射影是AP,所以直线AD与平面ABE所成角是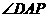
在 中,
中,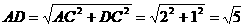 ,
,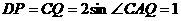
所以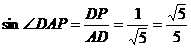
20.(本题满分14分)设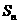 为数列
为数列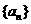 的前
的前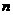 项和,
项和,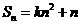 ,
,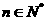 ,其中
,其中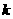 是常数.
是常数.
(I) 求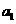 及
及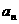 ;
;
(II)若对于任意的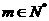 ,
,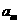 ,
,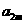 ,
,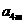 成等比数列,求
成等比数列,求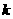 的值.
的值.
20、解析:(Ⅰ)当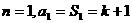 ,
, 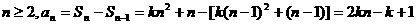 (
( )
)
经验,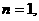 (
( )式成立,
)式成立, 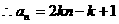
(Ⅱ)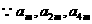 成等比数列,
成等比数列,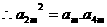 ,即
,即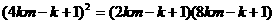 ,整理得:
,整理得: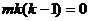 ,对任意的
,对任意的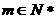 成立,
成立, 
21.(本题满分15分)已知函数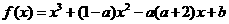
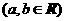 .
.
(I)若函数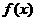 的图象过原点,且在原点处的切线斜率是
的图象过原点,且在原点处的切线斜率是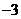 ,求
,求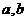 的值;
的值;
(II)若函数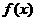 在区间
在区间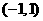 上不单调,求
上不单调,求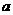 的取值范围.
的取值范围.
解析:(Ⅰ)由题意得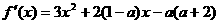
又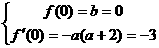 ,解得
,解得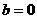 ,
,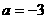 或
或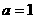
(Ⅱ)函数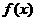 在区间
在区间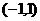 不单调,等价于
不单调,等价于
导函数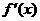 在
在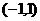 既能取到大于0的实数,又能取到小于0的实数
既能取到大于0的实数,又能取到小于0的实数
即函数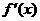 在
在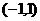 上存在零点,根据零点存在定理,有
上存在零点,根据零点存在定理,有
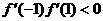 , 即:
, 即: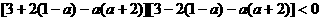
整理得: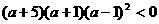 ,解得
,解得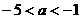
22.(本题满分15分)已知抛物线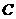 :
: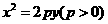 上一点
上一点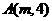 到其焦点的距离为
到其焦点的距离为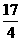 .
.
(I)求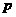 与
与 的值;
的值;
(II)设抛物线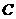 上一点
上一点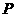 的横坐标为
的横坐标为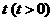 ,过
,过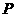 的直线交
的直线交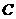 于另一点
于另一点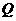 ,交
,交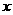 轴于点
轴于点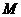 ,过点
,过点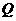 作
作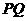 的垂线交
的垂线交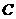 于另一点
于另一点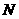 .若
.若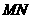 是
是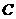 的切线,求
的切线,求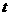 的最小值.
的最小值.
22.解析(Ⅰ)由抛物线方程得其准线方程: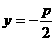 ,根据抛物线定义
,根据抛物线定义
点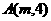 到焦点的距离等于它到准线的距离,即
到焦点的距离等于它到准线的距离,即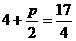 ,解得
,解得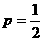
 抛物线方程为:
抛物线方程为: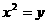 ,将
,将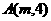 代入抛物线方程,解得
代入抛物线方程,解得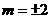
(Ⅱ)由题意知,过点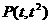 的直线
的直线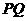 斜率存在且不为0,设其为
斜率存在且不为0,设其为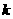 。
。
则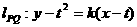 ,当
,当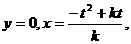 则
则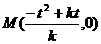 。
。
联立方程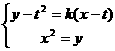 ,整理得:
,整理得: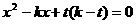
即: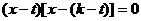 ,解得
,解得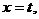 或
或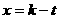
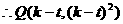 ,而
,而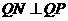 ,
, 直线
直线 斜率为
斜率为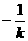
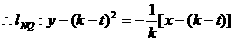 ,联立方程
,联立方程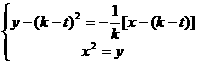
整理得: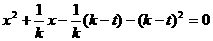 ,即:
,即: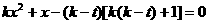
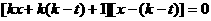 ,解得:
,解得: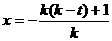 ,或
,或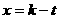
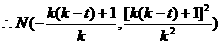 ,
,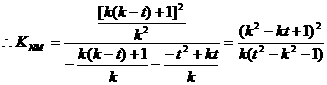
而抛物线在点N处切线斜率: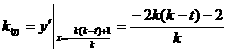
 MN是抛物线的切线,
MN是抛物线的切线,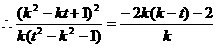 , 整理得
, 整理得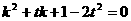
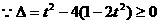 ,解得
,解得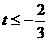 (舍去),或
(舍去),或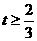 ,
,