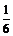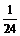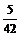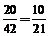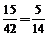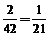(单词翻译:单击)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设集合A={x|1<x<4},B={x|x 2-2x-3≤0},则A∩( RB)=
RB)=
A.(1,4) B.(3,4) C.(1,3) D.(1,2)
【解析】A=(1,4),B=(-3,1),则A∩(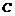 RB)=(1,4).
RB)=(1,4).
【答案】A
2.已知i是虚数单位,则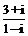 =
=
A.1-2i B.2-i C.2+i D.1+2i
【解析】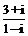 =
=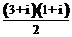 =
=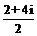 =1+2i.
=1+2i.
【答案】D
3.设a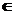 R,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的
R,则“a=1”是“直线l1:ax+2y-1=0与直线l2:x+(a+1)y+4=0平行”的
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
【解析】当a=1时,直线l1:x+2y-1=0与直线l2:x+2y+4=0显然平行;若直线l1与直线l2平行,则有: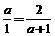 ,解之得:a=1 or a=﹣2.所以为充分不必要条件.
,解之得:a=1 or a=﹣2.所以为充分不必要条件.
【答案】A
4.把函数y=cos2x+1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变),然后向左平移1个单位长度,再向下平移1个单位长度,得到的图像是
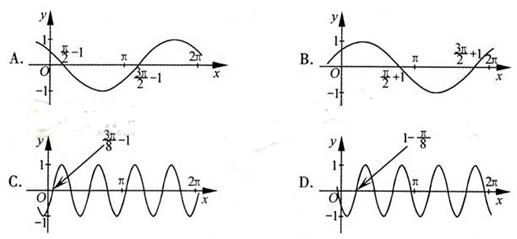
【解析】把函数y=cos2x+1的图像上所有点的横坐标伸长到原来的2倍(纵坐标不变)得:y1=cosx+1,向左平移1个单位长度得:y2=cos(x—1)+1,再向下平移1个单位长度得:y3=cos(x—1).令x=0,得:y3>0;x=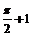 ,得:y3=0;观察即得答案.
,得:y3=0;观察即得答案.
【答案】B
5.设a,b是两个非零向量.
A.若|a+b|=|a|-|b|,则a⊥b
B.若a⊥b,则|a+b|=|a|-|b|
C.若|a+b|=|a|-|b|,则存在实数λ,使得a=λb
D.若存在实数λ,使得a=λb,则|a+b|=|a|-|b|
【解析】利用排除法可得选项C是正确的,∵|a+b|=|a|-|b|,则a,b共线,即存在实
数λ,使得a=λb.如选项A:|a+b|=|a|-|b|时,a,b可为异向的共线向量;选项B:若a⊥b,由正方形得|a+b|=|a|-|b|不成立;选项D:若存在实数λ,使得a=λb,a,b可为同向的共线向量,此时显然|a+b|=|a|-|b|不成立.
【答案】C
6.若从1,2,2,…,9这9个整数中同时取4个不同的数,其和为偶数,则不同的取法共有
A.60种 B.63种 C.65种 D.66种
【解析】1,2,2,…,9这9个整数中有5个奇数,4个偶数.要想同时取4个不同的数其和为偶数,则取法有:
4个都是偶数:1种;
2个偶数,2个奇数: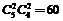 种;
种;
4个都是奇数: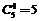 种.
种.
∴不同的取法共有66种.
【答案】D
7.设S n是公差为d(d≠0)的无穷等差数列{a n}的前n项和,则下列命题错误的是
A.若d<0,则数列{S n}有最大项
B.若数列{S n}有最大项,则d<0
C.若数列{S n}是递增数列,则对任意的n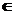 N*,均有S n>0
N*,均有S n>0
D.若对任意的n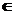 N*,均有S n>0,则数列{S n}是递增数列
N*,均有S n>0,则数列{S n}是递增数列
【解析】选项C显然是错的,举出反例:—1,0,1,2,3,….满足数列{S n}是递增数列,但是S n>0不成立.
【答案】C
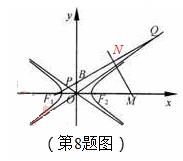
8.如图,F1,F2分别是双曲线C: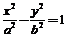 (a,b>0)的左右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是
(a,b>0)的左右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M.若|MF2|=|F1F2|,则C的离心率是
A.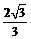 B.
B.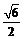
C.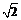 D.
D.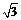
【解析】如图:|OB|=b,|O F1|=c.∴kPQ=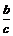 ,kMN=﹣
,kMN=﹣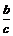 .
.
直线PQ为:y=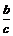 (x+c),两条渐近线为:y=
(x+c),两条渐近线为:y=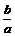 x.由
x.由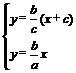 ,得:Q(
,得:Q(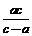 ,
,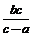 );由
);由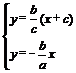 ,得:P(
,得:P(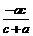 ,
,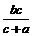 ).∴直线MN为:y-
).∴直线MN为:y-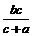 =﹣
=﹣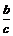 (x-
(x-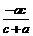 ),
),
令y=0得:xM=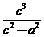 .又∵|MF2|=|F1F2|=2c,∴3c=xM=
.又∵|MF2|=|F1F2|=2c,∴3c=xM=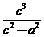 ,解之得:
,解之得: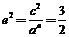 ,即e=
,即e=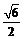 .
.
【答案】B
9.设a>0,b>0.
A.若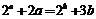 ,则a>b
,则a>b
B.若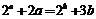 ,则a<b
,则a<b
C.若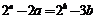 ,则a>b
,则a>b
D.若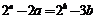 ,则a<b
,则a<b
【解析】若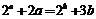 ,必有
,必有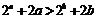 .构造函数:
.构造函数: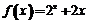 ,则
,则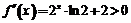 恒成立,故有函数
恒成立,故有函数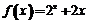 在x>0上单调递增,即a>b成立.其余选项用同样方法排除.
在x>0上单调递增,即a>b成立.其余选项用同样方法排除.
【答案】A
10.已知矩形ABCD,AB=1,BC=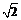 .将
.将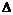 ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
ABD沿矩形的对角线BD所在的直线进行翻着,在翻着过程中,
A.存在某个位置,使得直线AC与直线BD垂直
B.存在某个位置,使得直线AB与直线CD垂直
C.存在某个位置,使得直线AD与直线BC垂直
D.对任意位置,三直线“AC与BD”,“AB与CD”,“AD与BC”均不垂直
【解析】最简单的方法是取一长方形动手按照其要求进行翻着,观察在翻着过程,即可知选项C是正确的.
【答案】C
非选择题部分(共100分)
二、填空题:本大题共7小题,每小题4分,共28分.
11.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于___________cm3.
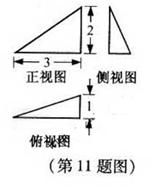
【解析】观察三视图知该三棱锥的底面为一直角三角形,右侧面也是一直角三角形.故体积等于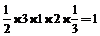 .
.
【答案】1
12.若程序框图如图所示,则该程序运行后输出的值是______________.
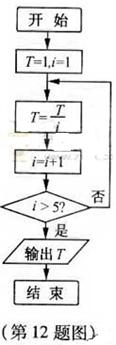
【解析】T,i关系如下图:
T | 1 |
|
|
|
|
i | 2 | 3 | 4 | 5 | 6 |
【答案】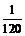
13.设公比为q(q>0)的等比数列{a n}的前n项和为{S n}.若
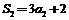 ,
,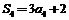 ,则q=______________.
,则q=______________.
【解析】将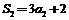 ,
,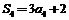 两个式子全部转化成用
两个式子全部转化成用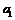 ,q表示的式子.
,q表示的式子.
即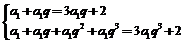 ,两式作差得:
,两式作差得: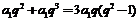 ,即:
,即: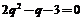 ,解之得:
,解之得: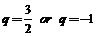 (舍去).
(舍去).
【答案】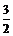
14.若将函数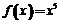 表示为
表示为
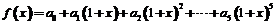
其中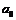 ,
,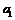 ,
,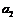 ,…,
,…,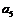 为实数,则
为实数,则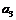 =______________.
=______________.
【解析】法一:由等式两边对应项系数相等.
即: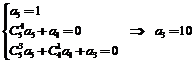 .
.
法二:对等式: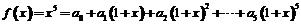 两边连续对x求导三次得:
两边连续对x求导三次得: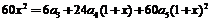 ,再运用赋值法,令
,再运用赋值法,令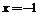 得:
得: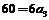 ,即
,即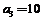 .
.
【答案】10
15.在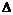 ABC中,M是BC的中点,AM=3,BC=10,则
ABC中,M是BC的中点,AM=3,BC=10,则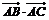 =______________.
=______________.
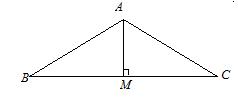
【解析】此题最适合的方法是特例法.假设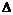 ABC是以AB=AC的等腰三角形,如图,AM=3,BC=10,AB=AC=
ABC是以AB=AC的等腰三角形,如图,AM=3,BC=10,AB=AC=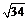 .
.
cos∠BAC=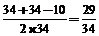 .
.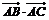 =
=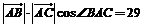
【答案】29
16.定义:曲线C上的点到直线l的距离的最小值称为曲线C到直线l的距离.已知曲线C1:y=x 2+a到直线l:y=x的距离等于C2:x 2+(y+4) 2 =2到直线l:y=x的距离,
则实数a=______________.
【解析】C2:x 2+(y+4) 2 =2,圆心(0,—4),圆心到直线l:y=x的距离为: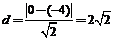 ,故曲线C2到直线l:y=x的距离为
,故曲线C2到直线l:y=x的距离为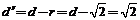 .
.
另一方面:曲线C1:y=x 2+a,令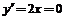 ,得:
,得: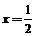 ,曲线C1:y=x 2+a到直线l:y=x的距离的点为(
,曲线C1:y=x 2+a到直线l:y=x的距离的点为(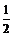 ,
,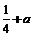 ),
),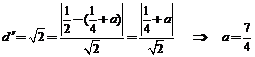 .
.
【答案】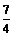
17.设a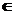 R,若x>0时均有[(a-1)x-1]( x 2-ax-1)≥0,则a=______________.
R,若x>0时均有[(a-1)x-1]( x 2-ax-1)≥0,则a=______________.
【解析】本题按照一般思路,则可分为一下两种情况:
(A)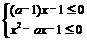 , 无解;
, 无解;
(B)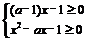 , 无解.
, 无解.
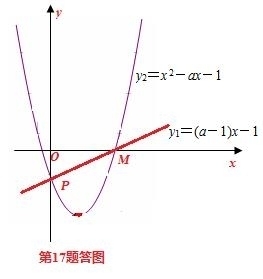
因为受到经验的影响,会认为本题可能是错题或者解不出本题.其实在x>0的整个区间上,我们可以将其分成两个区间(为什么是两个?),在各自的区间内恒正或恒负.(如下答图)
我们知道:函数y1=(a-1)x-1,y2=x 2-ax-1都过定点P(0,1).
考查函数y1=(a-1)x-1:令y=0,得M(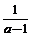 ,0),还可分析得:a>1;
,0),还可分析得:a>1;
考查函数y2=x 2-ax-1:显然过点M(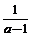 ,0),代入得:
,0),代入得: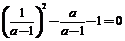 ,解之得:
,解之得: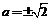 ,舍去
,舍去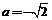 ,得答案:
,得答案: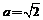 .
.
【答案】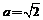
三、解答题:本大题共5小题,共72分,解答应写出文字说明、证明过程或演算步骤.
18.(本小题满分14分)在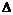 ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=
ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=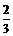 ,
,
sinB=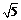 cosC.
cosC.
(Ⅰ)求tanC的值;
(Ⅱ)若a=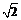 ,求
,求 ABC的面积.
ABC的面积.
【解析】本题主要考察三角恒等变换,正弦定理,余弦定理及三角形面积求法等知识点。
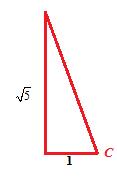
(Ⅰ)∵cosA=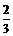 >0,∴sinA=
>0,∴sinA=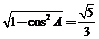 ,
,
又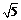 cosC=sinB=sin(A+C)=sinAcosC+sinCcosA
cosC=sinB=sin(A+C)=sinAcosC+sinCcosA
=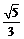 cosC+
cosC+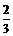 sinC.
sinC.
整理得:tanC=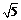 .
.
(Ⅱ)由图辅助三角形知:sinC=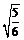 .
.
又由正弦定理知: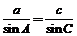 ,
,
故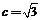 . (1)
. (1)
对角A运用余弦定理:cosA=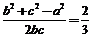 . (2)
. (2)
解(1) (2)得: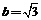 or b=
or b=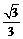 (舍去).
(舍去).
∴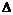 ABC的面积为:S=
ABC的面积为:S=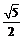 .
.
【答案】(Ⅰ) 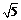 ;(Ⅱ)
;(Ⅱ) 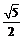 .
.
19.(本小题满分14分)已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.
(Ⅰ)求X的分布列;
(Ⅱ)求X的数学期望E(X).
【解析】本题主要考察分布列,数学期望等知识点。
(Ⅰ) X的可能取值有:3,4,5,6.
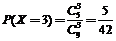 ;
; 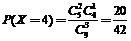 ;
;
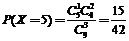 ;
; 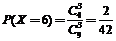 .
.
故,所求X的分布列为
X | 3 | 4 | 5 | 6 |
P |
|
|
|
|
(Ⅱ) 所求X的数学期望E(X)为:
E(X)=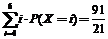 .
.
【答案】(Ⅰ)见解析;(Ⅱ) 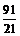 .
.
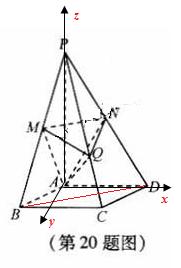
20.(本小题满分15分)如图,在四棱锥P—ABCD中,底面是边长为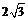 的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=
的菱形,且∠BAD=120°,且PA⊥平面ABCD,PA=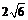 ,M,N分别为PB,PD的中点.
,M,N分别为PB,PD的中点.
(Ⅰ)证明:MN∥平面ABCD;
(Ⅱ) 过点A作AQ⊥PC,垂足为点Q,求二面角A—MN—Q的平面角的余弦值.
【解析】本题主要考察线面平行的证明方法,建系求二面角等知识点。
(Ⅰ)如图连接BD.
∵M,N分别为PB,PD的中点,
∴在 PBD中,MN∥BD.
PBD中,MN∥BD.
又MN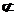 平面ABCD,
平面ABCD,
∴MN∥平面ABCD;
(Ⅱ)如图建系:
A(0,0,0),P(0,0,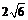 ),M(
),M(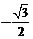 ,
,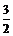 ,0),
,0),
N(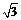 ,0,0),C(
,0,0),C(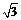 ,3,0).
,3,0).
设Q(x,y,z),则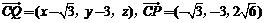 .
.
∵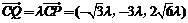 ,∴
,∴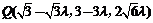 .
.
由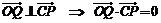 ,得:
,得: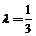 . 即:
. 即: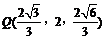 .
.
对于平面AMN:设其法向量为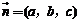 .
.
∵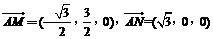 .
.
则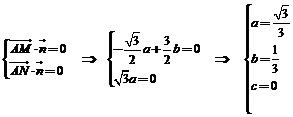 . ∴
. ∴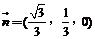 .
.
同理对于平面AMN得其法向量为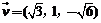 .
.
记所求二面角A—MN—Q的平面角大小为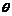 ,
,
则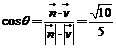 .
.
∴所求二面角A—MN—Q的平面角的余弦值为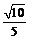 .
.
【答案】(Ⅰ)见解析;(Ⅱ) 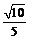 .
.
21.(本小题满分15分)如图,椭圆C: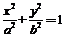 (a>b>0)的离心率为
(a>b>0)的离心率为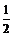 ,其左焦点到点P(2,1)的距离为
,其左焦点到点P(2,1)的距离为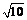 .不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
.不过原点O的直线l与C相交于A,B两点,且线段AB被直线OP平分.
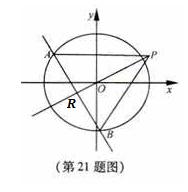
(Ⅰ)求椭圆C的方程;
(Ⅱ) 求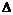 ABP的面积取最大时直线l的方程.
ABP的面积取最大时直线l的方程.
【解析】
(Ⅰ)由题: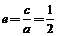 ; (1)
; (1)
左焦点(﹣c,0)到点P(2,1)的距离为: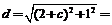
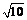 . (2)
. (2)
由(1) (2)可解得: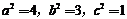 .
.
∴所求椭圆C的方程为: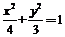 .
.
(Ⅱ)易得直线OP的方程:y=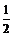 x,设A(xA,yA),B(xB,yB),R(x0,y0).其中y0=
x,设A(xA,yA),B(xB,yB),R(x0,y0).其中y0=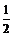 x0.
x0.
∵A,B在椭圆上,
∴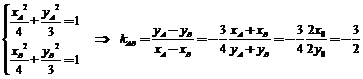 .
.
设直线AB的方程为l:y=﹣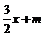 (m≠0),
(m≠0),
代入椭圆: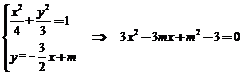 .
.
显然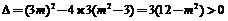 .
.
∴﹣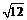 <m<
<m<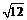 且m≠0.
且m≠0.
由上又有: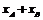 =m,
=m,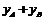 =
=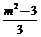 .
.
∴|AB|=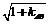 |
|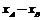 |=
|=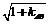
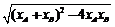 =
=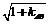
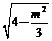 .
.
∵点P(2,1)到直线l的距离为: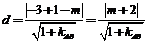 .
.
∴S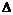 ABP=
ABP=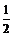 d|AB|=
d|AB|=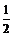 |m+2|
|m+2|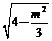 ,
,
当|m+2|=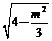 ,即m=﹣3 or m=0(舍去)时,(S
,即m=﹣3 or m=0(舍去)时,(S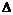 ABP)max=
ABP)max=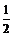 .
.
此时直线l的方程y=﹣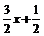 .
.
【答案】 (Ⅰ) 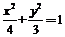 ;(Ⅱ) y=﹣
;(Ⅱ) y=﹣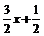 .
.
21.(本小题满分14分)已知a>0,b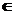 R,函数
R,函数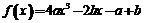 .
.
(Ⅰ)证明:当0≤x≤1时,
(ⅰ)函数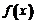 的最大值为|2a-b|﹢a;
的最大值为|2a-b|﹢a;
(ⅱ) 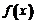 +|2a-b|﹢a≥0;
+|2a-b|﹢a≥0;
(Ⅱ) 若﹣1≤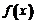 ≤1对x
≤1对x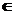 [0,1]恒成立,求a+b的取值范围.
[0,1]恒成立,求a+b的取值范围.
【解析】本题主要考察不等式,导数,单调性,线性规划等知识点及综合运用能力。
(Ⅰ)
(ⅰ)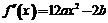 .
.
当b≤0时,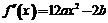 >0在0≤x≤1上恒成立,
>0在0≤x≤1上恒成立,
此时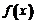 的最大值为:
的最大值为: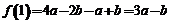 =|2a-b|﹢a;
=|2a-b|﹢a;
当b>0时,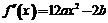 在0≤x≤1上的正负性不能判断,
在0≤x≤1上的正负性不能判断,
此时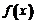 的最大值为:
的最大值为:
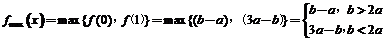 =|2a-b|﹢a;
=|2a-b|﹢a;
综上所述:函数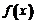 在0≤x≤1上的最大值为|2a-b|﹢a;
在0≤x≤1上的最大值为|2a-b|﹢a;
(ⅱ) 要证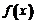 +|2a-b|﹢a≥0,即证
+|2a-b|﹢a≥0,即证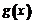 =﹣
=﹣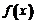 ≤|2a-b|﹢a.
≤|2a-b|﹢a.
亦即证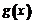 在0≤x≤1上的最大值小于(或等于)|2a-b|﹢a,
在0≤x≤1上的最大值小于(或等于)|2a-b|﹢a,
∵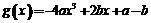 ,∴令
,∴令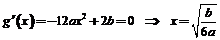 .
.
当b≤0时,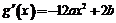 <0在0≤x≤1上恒成立,
<0在0≤x≤1上恒成立,
此时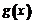 的最大值为:
的最大值为: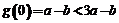 =|2a-b|﹢a;
=|2a-b|﹢a;
当b<0时,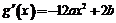 在0≤x≤1上的正负性不能判断,
在0≤x≤1上的正负性不能判断,
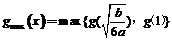
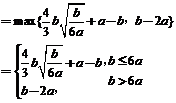
≤|2a-b|﹢a;
综上所述:函数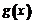 在0≤x≤1上的最大值小于(或等于)|2a-b|﹢a.
在0≤x≤1上的最大值小于(或等于)|2a-b|﹢a.
即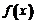 +|2a-b|﹢a≥0在0≤x≤1上恒成立.
+|2a-b|﹢a≥0在0≤x≤1上恒成立.
(Ⅱ)由(Ⅰ)知:函数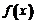 在0≤x≤1上的最大值为|2a-b|﹢a,
在0≤x≤1上的最大值为|2a-b|﹢a,
且函数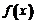 在0≤x≤1上的最小值比﹣(|2a-b|﹢a)要大.
在0≤x≤1上的最小值比﹣(|2a-b|﹢a)要大.
∵﹣1≤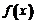 ≤1对x
≤1对x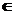 [0,1]恒成立,
[0,1]恒成立,
∴|2a-b|﹢a≤1.
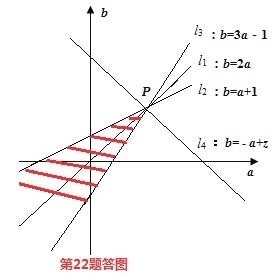
取b为纵轴,a为横轴.
则可行域为: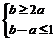 和
和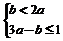 ,目标函数为z=a+b.
,目标函数为z=a+b.
作图如下:
由图易得:当目标函数为z=a+b过P(1,2)时,有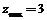 .
.
∴所求a+b的取值范围为: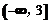 .
.
【答案】(Ⅰ) 见解析;(Ⅱ) 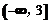 .
.