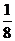(单词翻译:单击)
第Ⅰ卷(共60分)
一、选择题:本大题共l0小题.每小题5分,共50分在每小题给出的四个选项中,只有一项是满足题目要求的.
(1)已知全集U=R,集合M={x||x-1|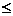 2},则
2},则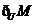 =
=
(A){x|-1<x<3} (B){x|-1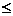 x
x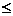 3}
3}
(C){x|x<-1或x>3} (D){x|x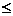 -1或x
-1或x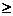 3}
3}
(2) 已知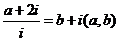
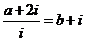 (a,b∈R),其中i为虚数单位,则a+b=
(a,b∈R),其中i为虚数单位,则a+b=
(A)-1 (B)1 (C)2 (D)3
(3)在空间,下列命题正确的是
(A)平行直线的平行投影重合
(B)平行于同一直线的两个平面平行
(C)垂直于同一平面的两个平面平行
(D)垂直于同一平面的两条直线平行
(4)设f(x)为定义在R上的奇函数,当x≥0时,f(x)=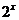 +2x+b(b为常数),则f(-1)=
+2x+b(b为常数),则f(-1)=
(A) 3 (B) 1 (C)-1 (D)-3
(5)已知 随机变量Z服从正态分布N(0,
随机变量Z服从正态分布N(0,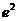 ),若P(Z>2)=0.023,则P(-2≤Z≤2)=
),若P(Z>2)=0.023,则P(-2≤Z≤2)=
(A)0.477 (B)0.625 (C)0.954 (D)0.977
(6)样本中共有五个个体,其值分别为a,0,1,2,3,,若该样本的平均值为1,则样本方差为
(A) 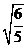 (B)
(B) 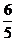 (C)
(C) 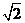 (D)2
(D)2
(7)由曲线y=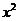 ,y=
,y=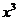 围成的封闭图形面积为
围成的封闭图形面积为
(A)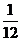 (B)
(B) 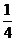 (C)
(C) 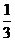 (D)
(D) 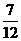
(8)某台小型晚会由6个节目组成,演出顺序有如下要求:节目甲必须排在第四位、节目乙不能排在第一位,节目丙必须排在最后一位,该台晚会节目演出顺序的编排方案共有
(A)36种 (B)42种 (C)48种 (D)54种
(9)设{an}是等比数列,则“a1<a2<a3”是数列{an}是递增数列的
(A)充分而不必要条件 (B)必要而不充分条件、
(C)充分必要条件 (D)既不充分也不必要条件
(10)设变量x、y满足约束条件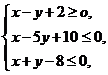 ,则目标函数z=3x-4y的最大值和最小值分别
,则目标函数z=3x-4y的最大值和最小值分别 为
为
(A)3,-11 (B) -3, -11
(C)11, -3 (D)11,3
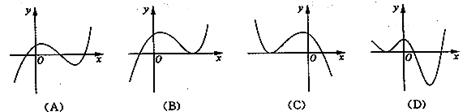
(11)函数y=2x -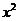 的图像大致是
的图像大致是
(12)定义平面向量之间的一种运算“⊙”如下:对任意的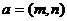 ,
,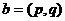 令
令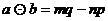 ,下面说法错误的是
,下面说法错误的是
(A)若a与b共线,则a⊙b=0
(B)a⊙b=b⊙a
(C)对任意的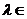 R,有(
R,有(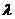 a)⊙b=
a)⊙b=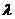 (a⊙b)
(a⊙b)
(D) (a⊙b)2+(a·b)2=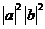
二、填空题:本大题共4小题,每小题4分,共16分.
(13)执行右图所示的程序框图,若输入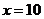 ,则输出
,则输出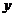 的值为 .
的值为 .
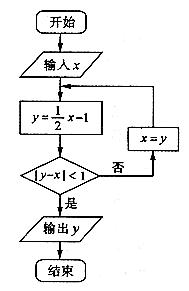
(14)若对任意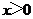 ,
,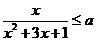 恒成立,则
恒成立,则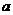 的取值范围是__________.
的取值范围是__________.
(15)在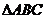 中,角
中,角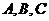 所对的边分别为a,b,c,若
所对的边分别为a,b,c,若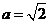 ,
,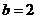 ,
,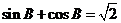 ,则角
,则角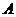 的大小为_________.
的大小为_________.
(16)已知圆C过点(1,0),且圆心在x轴的正半轴上,直线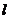 :
: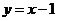 被圆C所截得的弦长为
被圆C所截得的弦长为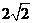 ,则过圆心且与直线
,则过圆心且与直线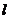 垂直的直线的方程为_________.
垂直的直线的方程为_________.
三、解答题:本大题共6小题,共74分.
(17)(本小题满分12分)
已知函数 ,其图象过点(
,其图象过点(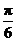 ,
,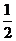 ).
).
(Ⅰ)求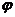 的值;
的值;
(Ⅱ)将函数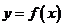 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的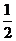 ,纵坐标不变,得到函数
,纵坐标不变,得到函数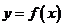 的图象,求函数
的图象,求函数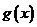 在[0,
在[0, 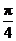 ]上的最大值和最小值.
]上的最大值和最小值.
(18)(本小题满分12分)
已知等差数列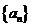 满足:
满足: ,
,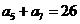 .
.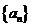 的前n项和为
的前n项和为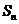 .
.
(Ⅰ)求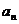 及
及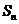 ;
;
(Ⅱ)令bn=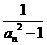 (n
(n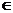 N*),求数列
N*),求数列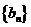 的前n项和
的前n项和 .
.
(19)(本小题满分12分)
如图,在五棱锥P—ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC, 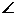 ABC=45°,AB=2
ABC=45°,AB=2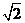 ,BC=2AE=4,三角形PAB是等腰三角形.
,BC=2AE=4,三角形PAB是等腰三角形.
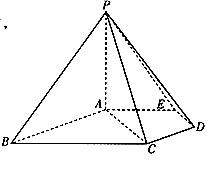
(Ⅰ)求证:平面PCD⊥平面PAC;
(Ⅱ)求直线PB与平面PCD所成角的大小;
(Ⅲ)求四棱锥P—ACDE的体积.
(20)(本小题满分12分)
某学校举行知识竞赛,第一轮选拔共设有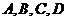 四个问题,规则如下:
四个问题,规则如下:
① 每位参加者计分器的初始分均为10分,答对问题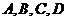 分别加1分、2分、3分、6分,答错任一题减2分;
分别加1分、2分、3分、6分,答错任一题减2分;
② 每回答一题,计分器显示累计分数,当累计分数小于8分时,答题结束,淘汰出局;当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局,当累计分数大于或等于14分时,答题结束,进入下一轮;当答完四题,累计分数仍不足14分时,答题结束,淘汰出局;
③ 每位参加者按问题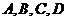 顺序作答,直至答题结束.
顺序作答,直至答题结束.
假设甲同学对问题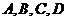 回答正确的概率依次为
回答正确的概率依次为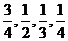 ,且各题回答正确与否相互之间没有影响.
,且各题回答正确与否相互之间没有影响.
(Ⅰ)求甲同学能进入下一轮的概率;
(Ⅱ)用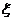 表示甲同学本轮答题结束时答题的个数,求
表示甲同学本轮答题结束时答题的个数,求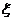 的分布列和数学的
的分布列和数学的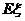 .
.
(21)(本小题满分12分)
如图,已知椭圆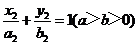 的离心率为
的离心率为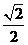 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点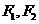 为顶点的三角形的周长为
为顶点的三角形的周长为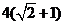 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设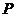 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线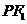 和
和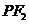 与椭圆的交点分别为
与椭圆的交点分别为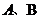 和
和 .
.
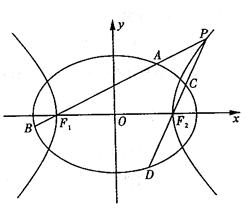
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线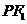 、
、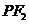 的斜率分别为
的斜率分别为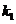 、
、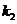 ,证明
,证明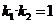 ;
;
(Ⅲ)是否存在常数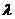 ,使得
,使得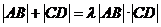 恒成立?若
恒成立?若 存在,求
存在,求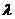 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(22)(本小题满分14分)
已知函数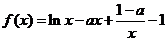
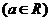 .
.
(Ⅰ)当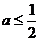 时,讨论
时,讨论 的单调性;
的单调性;
(Ⅱ)设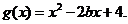 当
当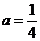 时,若对任意
时,若对任意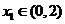 ,存在
,存在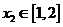 ,使
,使
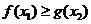 ,求实数
,求实数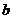 取值范围.
取值范围.
山东理数答案
一.选择题
1.C 2.B 3.D 4.D 5.C 6.D 7.A 8.B 9.C 10.A 11.A 12.B
二.填空题
13.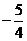 14.
14.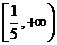 15.
15.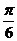 16.
16.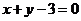
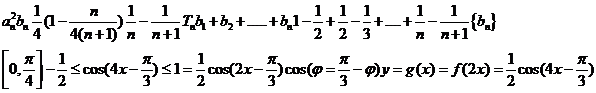
三.解答题

(Ⅱ)由(Ⅰ)知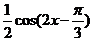 ,将函数
,将函数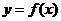 的图
的图 像上各点的横坐标缩短到原来的
像上各点的横坐标缩短到原来的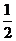 ,纵坐标
,纵坐标 不变,得到函数
不变,得到函数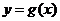 的图象,可知
的图象,可知
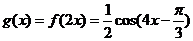
因为 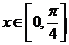 ,
,
所以 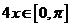 ,
,
因此 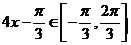 ,
,
故 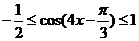 。
。
所以 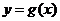 在
在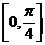 上的最大值和最小值分别为
上的最大值和最小值分别为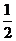 和
和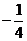 .
.
(18)本小题主要考查等差数列的基本知识,考查逻辑推理、等价变形和运算能力。
解:(Ⅰ) 设等差数列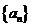 的首项为
的首项为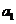 ,公差为d
,公差为d

所以数列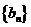 的前n项和
的前n项和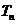 =
=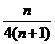
(19)本小题主要考察空间中的基本关系,考察线面垂直、面面垂直的判定以及线面角和集合体体积的计算,考查识图能力、空间想象力和逻辑推理能力,满分12分
(|)证明:
在△ABC中,因为∠ABC=45°,BC=4,AB=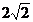 ,
,
所以AC2=AB+BC2 -2AB·BC·cos45°=8
-2AB·BC·cos45°=8
因此 AC=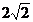 ,
,
故BC2=AC2+AB2,
所以∠BAC=90°----------------------------------------------------
又PA⊥平面ABCDE,AB∥CD,
所以CD⊥PA,CD⊥AC,
又 PA,AC 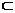 平面PAC,且PA
平面PAC,且PA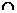 AC
AC =A,
=A,
所以 CD⊥PAC,又 CD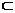 平面PCD,
平面PCD,
所以 平面PCD⊥平面PAC--------------------------------------------

则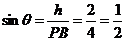 ,
,
又 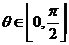 ,
,
所以 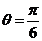
解法二:
由(|)知AB,AC,AP两两相互垂直,分别以AB、AC、AP为x轴、y轴、z轴建立如图所示的空间直角坐标系,由于△PAB是等腰三角形,
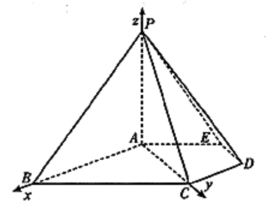 所以 PA=AB=
所以 PA=AB=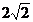 ,
,
又AC=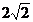 ,
,

所以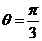 ,
,
因此直线 PB与平面PCD所成的角为
PB与平面PCD所成的角为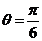
(Ⅲ)因为AC∥ED,CD⊥AC,
所以 四边形ACDE是直角梯形,
因为 AE=2,∠ABC=45°,AE∥BC,
所以 ∠BAE=135°,
因此 ∠CAE=45°,
故 CD=AE·sin45°==2×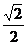 =
=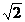 ,
,
所以 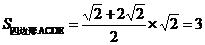
又 PA⊥平面ABCDE,
所以 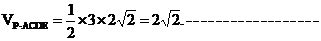
(20)本小题主要考查离散型随机变量的分布列和数学期望,考查对立事件、独立事件的概率和求解方法,考查用概率知识解决实际问题的能力.
解:设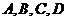 分别为第一、二、三、四个问题.用
分别为第一、二、三、四个问题.用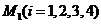 表示甲同学第
表示甲同学第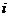 个问题回答正确,用
个问题回答正确,用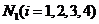 表示甲同学第
表示甲同学第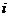 个问题回答错误,则
个问题回答错误,则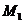 与
与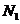 是对立事件
是对立事件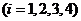 .由题意得
.由题意得
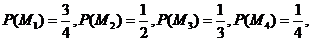
所以
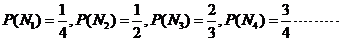
(Ⅰ)记“甲同学能进入下一轮”为事件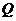 ,
,
则
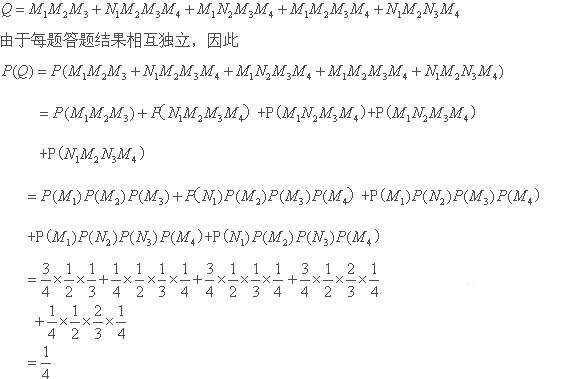
(Ⅱ)由题意,随机变量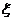 的可能取值为:
的可能取值为: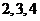 .
.
由于每题答题结果相互独立,
所以
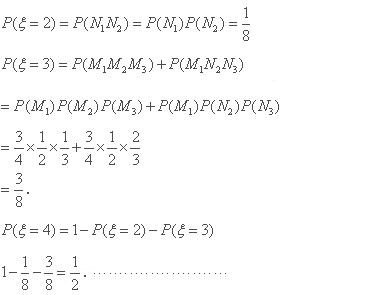
因此 随机变量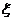 的分布列为
的分布列为
|
|
|
|
|
|
|
|
所以
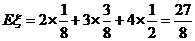 .
.
(21)本小题主要考查椭圆、双曲线的基本概念和基本性质。考查直线和椭圆的位置关系,考查坐标化、定值和存在性问题,考查数行结合思想和探求问题的能力。
解(Ⅰ)设椭圆的半焦距为c,由题意知: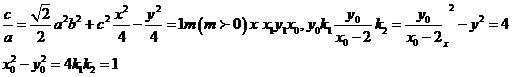
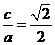 ,2a+2c=4(
,2a+2c=4(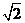 +1)
+1)
所以a=2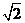 ,c=2,
,c=2,
又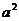 =
=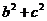 ,因此b=2。
,因此b=2。
故 椭圆的标准方程为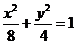
由题意设等轴双曲线的标准方程为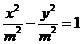
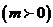 ,因为等轴双曲线的顶点是椭圆的焦点。
,因为等轴双曲线的顶点是椭圆的焦点。
所以m=2,
因此 双曲线的标准方程为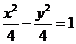
(Ⅱ)设A(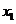 ,
,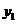 ),B(
),B(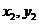 ),P(
),P(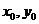 ),
),
则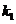 =
=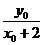 ,
,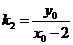 。
。
因为点P在双曲线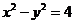 上,所以
上,所以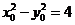 。
。
因此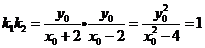 ,
,
即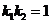

同理可 得
得
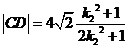 .
.
则 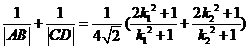 ,
,
又 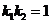 ,
,
所以 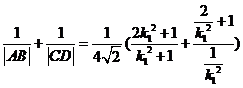
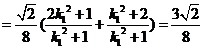 .
.
故 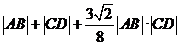
因此 存在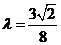 ,使
,使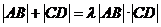 恒成立.
恒成立.
(22)本小题主要考查导数的概念以及利用导数研究函数性质的能力,考查分类讨论思想、数形结合思想、等价变换思想,以及综合运用知识解决新情境、新问题的能力。
解:(Ⅰ)因为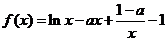 ,
,
所以 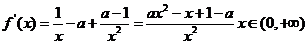 ,
,
令 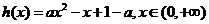 ,
,

①当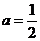 时,
时,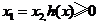 恒成立,此时
恒成立,此时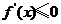 ,函数
,函数  在
在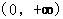 上单调递减;
上单调递减;
②当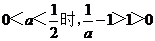 ,
,
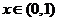 时,
时,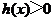 ,此时
,此时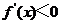 ,函数
,函数 单调递减;
单调递减;
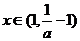 时
时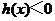 ,此时
,此时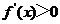 ,函数
,函数  单调递增;
单调递增;
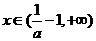 时,
时,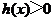 ,此时
,此时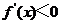 ,函数
,函数 单调递减;
单调递减;
③当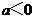 时,由于
时,由于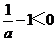 ,
,
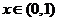 ,
,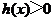 ,此时
,此时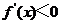 ,函数
,函数  单调递减;
单调递减;
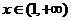 时,
时,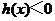 ,此时
,此时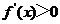 ,函数
,函数 单调递增.
单调递增.
综上所述:

(Ⅱ)因为a=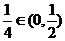 ,由(Ⅰ)知,
,由(Ⅰ)知,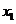 =1,
=1,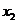 =3
=3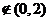 ,当
,当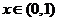 时,
时,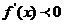 ,函数
,函数 单调递减;
单调递减;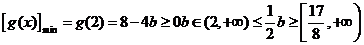 当
当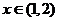 时,
时,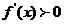 ,函数
,函数 单调递增,所以
单调递增,所以 在(0,2)上的最小值为
在(0,2)上的最小值为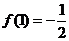 。
。
由于“对任意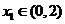 ,存在
,存在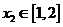 ,使
,使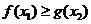 ”等价于
”等价于
“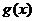 在
在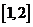 上的最小值不大于
上的最小值不大于 在(0,2)上的最小值
在(0,2)上的最小值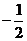 ”(*)
”(*)
又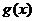 =
=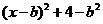 ,
,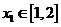 ,所以
,所以
①当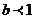 时,因为
时,因为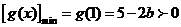 ,此时与(*)矛盾
,此时与(*)矛盾
②当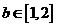 时,因为
时,因为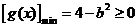 ,同样与(*)矛盾
,同样与(*)矛盾
③当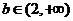 时,因为
时,因为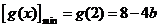 ,解不等式8-4b
,解不等式8-4b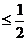 ,可得
,可得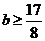
综上,b的取值范围是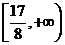 。
。