(单词翻译:单击)
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设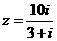 ,则z的共轭复数为 ( )
,则z的共轭复数为 ( )
A.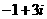 B.
B.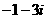 C.
C.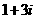 D.
D.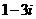

2.设集合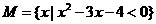 ,
,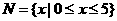 ,则
,则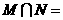 ( )
( )
A.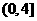 B.
B.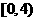 C.
C.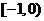 D.
D.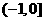

3.设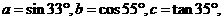 则 ( )
则 ( )
A.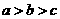 B.
B.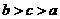 C.
C.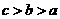 D.
D.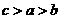

4.若向量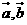 满足:
满足: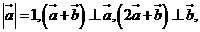 则
则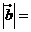 ( )
( )
A.2 B.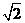 C.1 D.
C.1 D.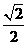

5.有6名男医生、5名女医生,从中选出2名男医生、1名女医生组成一个医疗小组,则不同的选法共有( )
A.60种 B.70种 C.75种 D.150种

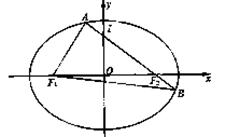
6.已知椭圆C: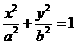
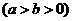 的左、右焦点为
的左、右焦点为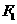 、
、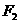 ,离心率为
,离心率为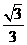 ,过
,过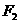 的直线
的直线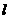 交C于A、B两点,若
交C于A、B两点,若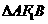 的周长为
的周长为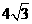 ,则C的方程为 ( )
,则C的方程为 ( )
A.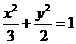 B.
B.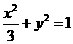 C.
C.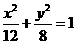 D.
D.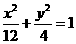
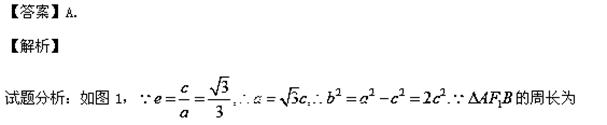

7.曲线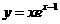 在点(1, 1)处切线的斜率等于 ( )
在点(1, 1)处切线的斜率等于 ( )
A.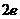 B.
B.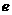 C.2 D.1
C.2 D.1

8.正四棱锥的顶点都在同一球面上,若该棱锥的高为4,底面边长为2,则该球的表面积为 ( )
A.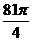 B.
B.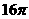 C.
C.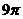 D.
D.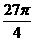
【答案】A.
| 图2 |
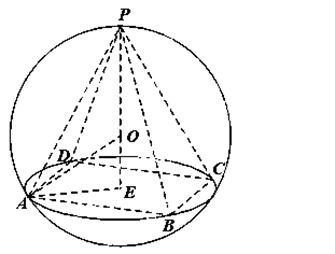
【解析】

考点:1.球的内接正四棱锥问题;2. 球的表面积的计算.
9.已知双曲线C的离心率为2,焦点为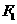 、
、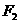 ,点A在C上,若
,点A在C上,若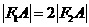 ,则
,则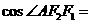 ( )
( )
A.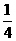 B.
B.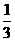 C.
C.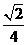 D.
D.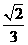

10.等比数列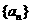 中,
中,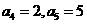 ,则数列
,则数列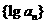 的前8项和等于 ( )
的前8项和等于 ( )
A.6 B.5 C.4 D.3

11.已知二面角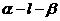 为
为 ,
,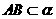 ,
,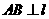 ,A为垂足,
,A为垂足,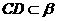 ,
,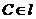 ,
,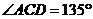 ,则异面直线
,则异面直线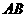 与
与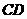 所成角的余弦值为 ( )
所成角的余弦值为 ( )
A.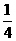 B.
B.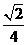 C.
C.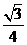 D.
D.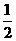
【答案】B.
【解析】

12.函数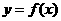 的图象与函数
的图象与函数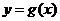 的图象关于直线
的图象关于直线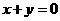 对称,则
对称,则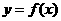 的反函数是( )
的反函数是( )
A.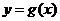 B.
B.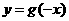 C.
C.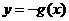 D.
D.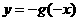

第Ⅱ卷(共90分)
二、填空题(每题5分,满分20分,将答案填在答题纸上)
13. 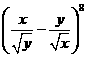 的展开式中
的展开式中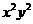 的系数为____________.
的系数为____________.
【答案】70.

14.设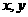 满足约束条件
满足约束条件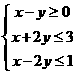 ,则
,则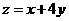 的最大值为___________.
的最大值为___________.

15.直线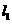 和
和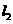 是圆
是圆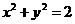 的两条切线,若
的两条切线,若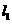 与
与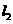 的交点为
的交点为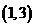 ,则
,则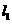 与
与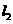 的夹角的正切值等于___________ .
的夹角的正切值等于___________ .
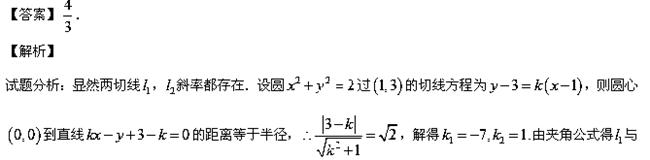
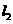 的夹角的正切值:
的夹角的正切值: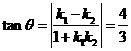 .
.
考点:1.直线与圆的位置关系(相切);2.两直线的夹角公式.
16.若函数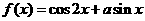 在区间
在区间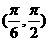 是减函数,则
是减函数,则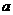 的取值范围是___________ .
的取值范围是___________ .

三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
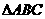 的内角A,B,C的对边分别为a,b,c,已知
的内角A,B,C的对边分别为a,b,c,已知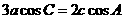 ,
,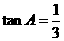 ,求B.
,求B.

18. (本小题满分12分)
等差数列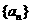 的前n项和为
的前n项和为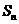 ,已知
,已知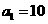 ,
,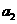 为整数,且
为整数,且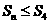 .
.
(I)求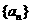 的通项公式;
的通项公式;
(II)设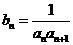 ,求数列
,求数列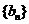 的前n项和
的前n项和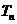 .
.

19. (本小题满分12分)
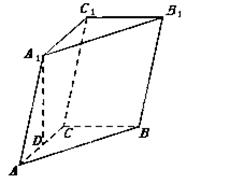
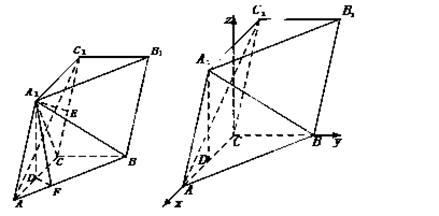
如图,三棱柱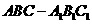 中,点
中,点 在平面ABC内的射影D在AC上,
在平面ABC内的射影D在AC上,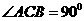 ,
,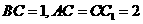 .
.
(I)证明: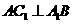 ;
;
(II)设直线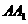 与平面
与平面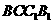 的距离为
的距离为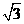 ,求二面角
,求二面角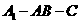 的大小.
的大小.



20. (本小题满分12分)
设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别为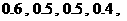 各人是否需使用设备相互独立.
各人是否需使用设备相互独立.
(I)求同一工作日至少3人需使用设备的概率;
(II)X表示同一工作日需使用设备的人数,求X的数学期望.


21.(本小题满分12分)
已知抛物线C: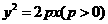 的焦点为F,直线
的焦点为F,直线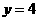 与y轴的交点为P,与C的交点为Q,且
与y轴的交点为P,与C的交点为Q,且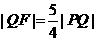 .
.
(I)求C的方程;
(II)过F的直线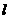 与C相交于A,B两点,若AB的垂直平分线
与C相交于A,B两点,若AB的垂直平分线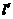 与C相较于M,N两点,且A,M,B,N四点在同一圆上,求
与C相较于M,N两点,且A,M,B,N四点在同一圆上,求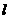 的方程.
的方程.
【答案】(I)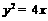 ;(II)直线
;(II)直线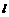 的方程为
的方程为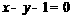 或
或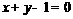 .
.


22. (本小题满分12分)
函数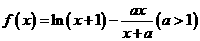 .
.
(I)讨论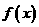 的单调性;
的单调性;
(II)设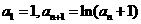 ,证明:
,证明: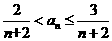 .
.
【答案】(I)(i)当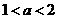 时,
时,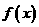 在
在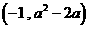 上是增函数,在
上是增函数,在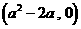 上是减函数,在
上是减函数,在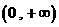 上是增函数;(ii)当
上是增函数;(ii)当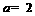 时,
时,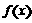 在
在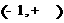 上是增函数;(iii)当
上是增函数;(iii)当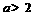 时,
时,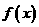 在是
在是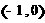 上是增函数,在
上是增函数,在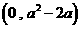 上是减函数,在
上是减函数,在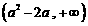 上是增函数;(II)详见试题分析.
上是增函数;(II)详见试题分析.



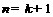 时有
时有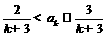 ,结论成立.根据(i)、(ii)知对任何
,结论成立.根据(i)、(ii)知对任何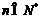 结论都成立.
结论都成立.
考点:1.利用导数研究函数的单调性;2.利用数学归纳法证明数列不等式.


