(单词翻译:单击)
一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分)
1.(3分)﹣2的绝对值是( )
A. ﹣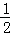 B. ﹣2 C.
B. ﹣2 C. 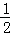 D. 2
D. 2
2.(3分)如图,下列图形中,是中心对称图形的是( )
A.  B.
B.  C.
C.  D.
D. 
3.(3分)﹣4a2b的次数是( )
A. 3 B. 2 C. 4 D. ﹣4
4.(3分)如果a<0,则下列式子错误的是( )
A. 5+a>3+a B. 5﹣a>3﹣a C. 5a>3a D. 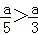
5.(3分)如图,三条直线相交于点O.若CO⊥AB,∠1=56°,则∠2等于( )
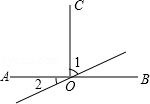
A. 30° B. 34° C. 45° D. 56°
6.(3分)某品牌鞋店在一个月内销售某款女鞋,各种尺码鞋的销量如下表所示:
尺码/厘米 | 22.5 | 23 | 23.5 | 24 | 24.5 |
销售量/双 | 35 | 40 | 30 | 17 | 8 |
通过分析上述数据,对鞋店业主的进货最有意义的是( )
A. 平均数 B. 众数 C. 中位数 D. 方差
7.(3分)在Rt△ABC中,∠C=90°,AB=10.若以点C为圆心,CB为半径的圆恰好经过AB的中点D,则AC=( )
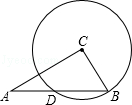
A. 5 B. 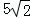 C.
C. 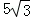 D. 6
D. 6
8.(3分)设a、b是直角三角形 的两条直角边,若该三角形的周长为6,斜边长为2.5,则ab的值是( )
的两条直角边,若该三角形的周长为6,斜边长为2.5,则ab的值是( )
A. 1.5 B. 2 C. 2.5 D. 3
2.5 D. 3
二、填空题(本大题共6个小题,每小题3分,满分18分)
9.(3分) 4的算术平方根是_________.
4的算术平方根是_________.
10.(3分)分解因式:2﹣2a2=__________.
11.(3分)函数的主要表示方法有________、________、________三种.
12.(3分)请将2、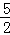 、
、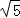 这三个数用“>”连结起来_______.
这三个数用“>”连结起来_______.
13.(3分)以下三组图形都是由四个等边三角形组成.能折成多面体的选项序号是_______.
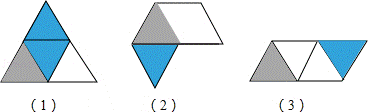
14.(3分)已知正方体的棱长为3,以它的下底面的外接圆为底、上底面对角线的交点为顶点构造一个圆锥体,那么这个圆锥体的体积是_______(π=3.14).
三、解答题(本大题共9个小题,满分58分)
15.(5分)
(1)计算: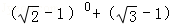
(2)计算: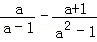 .
.
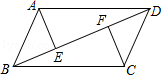
16.(5分)(2![]() 013•德宏州)如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BF=DE.
013•德宏州)如图,在平行四边形ABCD中,E、F是对角线BD上的两点,且BF=DE.
求证:AE∥CF.
17.(6分)某农户原有15头大牛和5头小牛,每天约用饲料325kg;两周后,由于经济效益好,该农户决定扩大养牛规模,又购进了10头大牛和5头小牛,这时每天约用饲料550kg.问每头大牛和每头小牛1天各需多少饲料?
18.(7分)某地州一个县市2012年考生中考数学成绩统计情况见如图表.
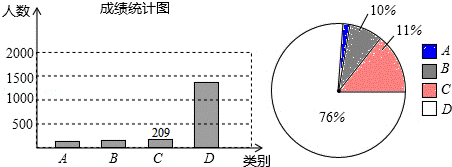
考试成绩等第表:
等第 | A:优秀 | B:良好 | C:及格 | D:不及格 |
成绩划分 | ≥135 | ≥105且<135 | ≥90且<105 | <90 |
根据以上图表所提供的信息,回答下列问题:
(1)求出该县市考生优秀等第的百分比;
(2)求出该县市达到良好及以上等第的考生人数;
(3)如果这个地州2012![]() 年考生人数约为14000人,用该县市考生的数学成绩做样本,估算出这个地州不及格等第的考生人数.
年考生人数约为14000人,用该县市考生的数学成绩做样本,估算出这个地州不及格等第的考生人数.
19.(7分)小明从家到学校上学,沿途需经过三个路口,每个路口都设有红、绿两种颜色的信号灯,在信号灯正常情况下:
(1)请用树状图列举小明遇到交通信号灯的所有情况;
(2)小明遇到两次绿色信号的概率有多大?
(3)小明红绿色两种信号都遇到的概率有多大?
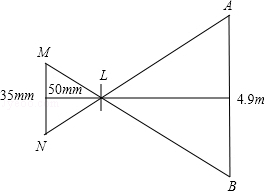
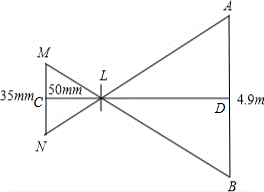
20.(6分)如图,是一个照相机成像的示意图.
(1)如果像高MN是35mm,焦距是50mm,拍摄的景物高度AB是4.9m,拍摄点离景物有多远?
(2)如果要完整的拍摄高度是2m的 景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少?
景物,拍摄点离景物有4m,像高不变,则相机的焦距应调整为多少?
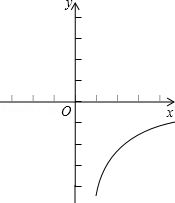
21.(6分)如图,是反比例函数y=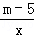 的图象的一支.根据给出的图象回答下列问题:
的图象的一支.根据给出的图象回答下列问题:
(1)该函数的图象位于哪几个象限?请确定m的取值范围;
(2)在这个函数图象的某一支上取点A(x1,y1)、B(x2,y2).如果y1<y2,那么x1与x2有怎样的大小关系?
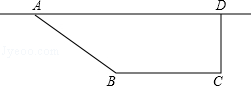
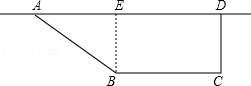
22.(7分)如图,要建造一个直角梯形的花圃.要求AD边靠墙,CD⊥AD,AB:CD=5:4,另外三边的和为20米.设AB的长为5x米.
(1)请求出AD的长(用含字母x的式子表示);
(2)若该花圃的面积为50米2,且周长不大于30米,求AB的长.
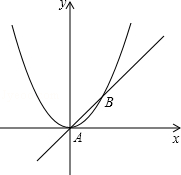
23.(9分)如图,已知直线y=x与抛物线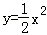 交于A、B两点.
交于A、B两点.
(1)求交点A、B的坐标;
(2)记一次函数y=x的函数值为y1,二次函数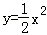 的函数值为y2.若y1>y2,求x的取值范围;
的函数值为y2.若y1>y2,求x的取值范围;
(3)在该抛物线上存在几个点,使得每个点与AB构成的三角形为等腰三角形?并求出不少于3个满足条件的点P的坐标.
一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分)
1.D
2.A
3.A
4.C
5.B
6.B
7.C
8.D
二、填空题(本大题共6个小题,每小题3分,满分18分)
9. 2 .
10. 2(1+a)(1﹣a) .
11. 列表法 、 图象法 、 解析式法 .
12. 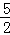 >
>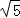 >2 .
>2 .
13. (1)(3) .
14. 9.42 .
三、解答题(本大题共9个小题,满分58分)
15.解:(1)原式=1+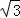 ﹣1=
﹣1=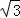 ;
;
(2)原式=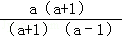 ﹣
﹣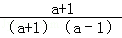 =
=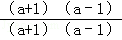 =1.
=1.
16.证明:∵平行四边形ABCD中,AD=BC,AD∥BC,
∴∠ADE=∠CBF.
∴在△ADE与△CBF中,
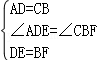 ,
,
∴△ADE≌△CBF(SAS),
∴∠AED=∠CFB,
∴AE∥CF.
17.解:设每头大牛1天需要饲料xkg,每头小牛1天需要饲料ykg,由题意,得
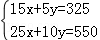 ,
,
解得: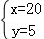 ,
,
答:每头大牛1天需要饲料20kg,每头小牛1天需要饲料5kg.
18.解:
(1)1﹣10%﹣11%﹣76%=1﹣97%=3%,所以,该县市考生优秀等第的百分比为3%;
(2)该县市的考生人数为:209÷11%=1900,达到良好及以上等![]() 第的考生人数为:1900×(3%+10%)=247;
第的考生人数为:1900×(3%+10%)=247;
(3)这个地州不及格等第的考生人数约为:14000×76%=10640.
19.解:(1)根据题意画出树状图如下:
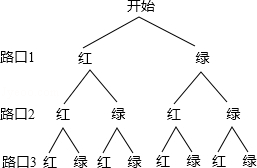
一共有8种情况;
(2)两次绿色信号的 情况数是3种,所以,P(两次绿色信号)=
情况数是3种,所以,P(两次绿色信号)=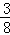 ;
;
(3)红绿色两种信号的情况有6种,所以,P(红绿色两种信号)=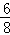 =
=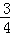 .
.
20.解:根据物体成像原理知:△LMN∽△LBA,
∴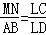 .
.
(1)∵像高MN是35mm,焦距是50mm,拍摄的景物高度AB是4![]() .9m,
.9m,
∴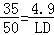 ,
,
解得:LD=7,
∴拍摄点距离景物7米;
(2)拍摄高度是2m的景物,拍摄点离景物有4m,像高不变,
∴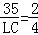 ,
,
解得:LC=70,
∴相机的焦距应调整为70mm.
21.解:(1)∵反比例函数图象关于原点对称,图中反比例函数图象位于第四象限,
∴函数图象位于第二、四象限,则m﹣5<0,
解得,m<5,即m的取值范围是m<5;
(2)由(1)知,函数图象位于第二、四象限.所以在每一个象限内,函数值y随自变量x增大而增大.
①当y1<y2<0时,x1<x2.
②当0<y1<y2,x1<x2.
③当y1<0<y2,x2<x1.
22.解:(1)作BE⊥AD于E,
∴∠AEB=∠DEB=90°.
∵CD⊥AD,
∴∠ADC=90°.
∵BC∥AD,
∴∠EBC=90°,
∴四边形BCDE是矩形,
∴BE=CD,BC=DE.
∵AB:CD=5:4,AB的长为5x米,
∴CD=4x米,
∴BE=4x,
在Rt△ABE中,由勾 股定理,得
股定理,得
AE=3x.
∵BC=20﹣5x﹣4x=20﹣9x,
∴DE=20﹣9x,
∴AD=20﹣9x+3x=20﹣6x
(2)由题意,得
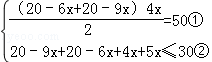 ,
,
由①,得
x1=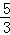 ,x2=1,
,x2=1,
由②,得
x≥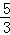 ,
,
∴x=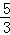 ,
,
AB=5×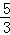 =
=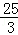 .
.
23.解:(1)如图,∵直线y=x与抛物线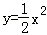 交于A、B两点,
交于A、B两点,
∴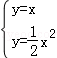 ,
,
解得,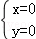 或
或
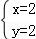 ,
,
∴A(0,0),B(2,2);
(2)由(1)知,A(0,0),B(2,2).
∵一次函数y=x的函数值为y1,二次函数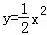 的函数值为y2.
的函数值为y2.
∴当y1>y2时,根据图象可知x的取值范围是:0<x<2;
(3)该抛物线上存在4个点,使得每个点与AB构成的三角形为等腰三角形.理由如下:
∵A(0,0),B(2,2),
∴B=2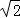 .
.
根据题意,可设P(x,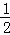 x2).
x2).
①当PA=PB时,点P是线段AB的中垂线与抛物线的交点.
易求线段AB的中垂线的解析式为y=﹣x+2,
则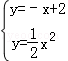 ,
,
解得,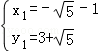 ,
,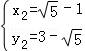 ,
,
∴P1(﹣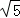 ﹣1,3+
﹣1,3+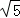 ),P2(
),P2(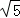 ﹣1,3﹣
﹣1,3﹣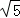 );
);
②当PA=AB时,根据抛物线的对称性知,点P与点B关于y轴对称,即P3(﹣2,2);
③当AB=PB时,点P4的位置如图所示.
综上所述,符号条件的点P有4个,其中P1(﹣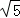 ﹣1,3+
﹣1,3+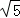 ),P2(
),P2(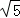 ﹣1,3﹣
﹣1,3﹣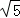 ),P3(﹣2,2).
),P3(﹣2,2).