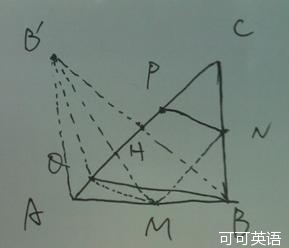
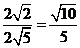(单词翻译:单击)
A卷(共100分)
第I卷(选择题,共30分)
一、选择题(本大题共10个小题,每小题3分,共30分,每小题均有四个选项,其中只有一项符合题目要求,答案涂在答题卡上)
1. 2的相反数是( )
A.2 B.-2 C.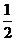 D.
D.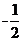
答案:B
解析:2的相反数为-2,较简单。
2.如图所示的几何体的俯视图可能是( )
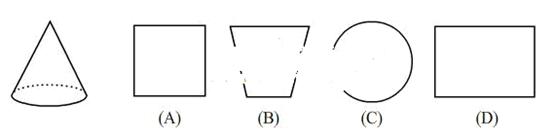
答案:C
解析:圆锥的俯视图为一个圆及圆心,圆锥的顶点俯视图是圆心(一个点)。
3.要使分式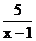 有意义,则X的取值范围是( )
有意义,则X的取值范围是( )
A.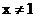 B.
B.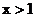 C.
C.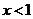 D.
D.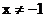
答案:A
解析:由分式的意义,得:x-1≠0,即x≠1,选A。
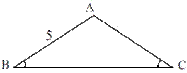
4.如图,在△ABC中,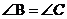 ,AB=5,则AC的长为( )
,AB=5,则AC的长为( )
A.2 B.3 C.4 D.5
答案:D
解析:由∠B=∠C,得AC=AB=5(等角对等边),故选D>
5.下列运算正确的是( )
A.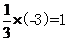 B.
B.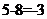 C.
C.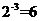 D.
D.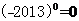
答案:B
解析: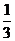 ×(-3)=-1,
×(-3)=-1,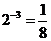 ,(-2013)0=1,故A、C、D都错,选B。
,(-2013)0=1,故A、C、D都错,选B。
6.参加成都市今年初三毕业会考的学生约为13万人,将13万用科学记数法表示应为( )
A.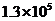 B.
B. 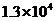 C.
C.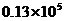 D.
D. 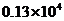
答案:A
解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数
13万=130000=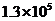
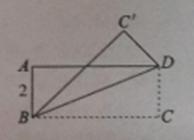
7.如图,将矩形ABCD沿对角线BD折叠,使点C与点C’重合。若AB=2,则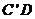 的长为( )
的长为( )
A.1 B.2 C.3 D.4
答案:B
解析:由折叠可知,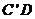 =CD=AB=2。
=CD=AB=2。

9.一元二次方程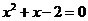 的根的情况是( )
的根的情况是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.只有一个实数根 D.没有实数根
答案:A
解析:因为△=12-4×1×(-2)=9>0,所以,原方程有两个不相等的实数根。
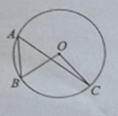
10. 如图,点A,B,C在
如图,点A,B,C在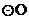 上,
上,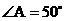 ,则
,则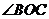 的度数为( )
的度数为( )
A.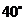 B.
B.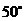 C.
C.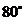 D.
D.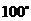
答案:D
解析:因为同弧所对的圆周角等于它所对圆心角的一半,所以,∠BOC=2∠BAC=100°,选D。
二、填空题(本大题4个小题,每个小题4分,共16分,答案写在答题卡上)
11.不等式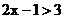 的解集为_________.
的解集为_________.
答案:x>2
解析:2x-1>3 ⇒2x>4 ⇒x>2
12.今年4月20日在雅安芦山县发生了7.0级的大地震,全川人民众志成城,抗震救灾,某班组织“捐零花钱,献爱心”活动,全班50名学生的捐款情况如图所示,则本次捐款金额众数是_______元.
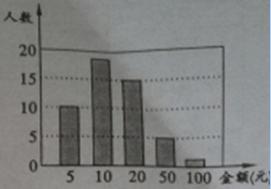
答案:10
解析:由图可知,捐款数为10元的最多人,故众数为10元。
13.如图,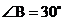 ,若AB∥CD,CB平分
,若AB∥CD,CB平分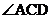 ,则
,则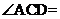 ______度.
______度.
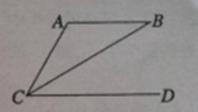
答案:60°
解析:∠ACD=2∠BCD=2∠ABC=60°
14.如图,某山坡的坡面AB=200米,坡角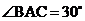 ,则该山坡的高BC的长为_____米。
,则该山坡的高BC的长为_____米。
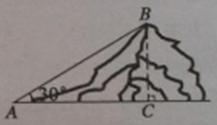
答案:100
解析:BC=AB·sin30°=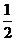 AB=100m
AB=100m
三、解答题(本大题6个小题,共54分.答案写在答题卡上)
15.(本小题满分12分,每小题6分)
(1)计算: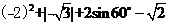
解析:
(1)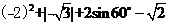
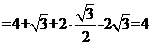
(2)解方程组:
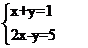 .
.
解析: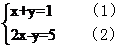
①式+②式有3x=6⇒x=2 代入①得y=-1
∴方程解为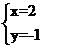
16.(本小题满分6分)
化简: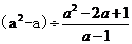 .
.
解析: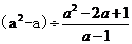
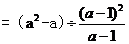
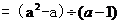
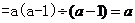
17.(本小题满分8分)
如图,在边长为1的小正方形组成的方格纸上,将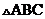 绕着点A顺时针旋转
绕着点A顺时针旋转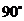 。
。
(1)画出旋转后的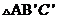 ;
;
(2)求线段AC在旋转过程中所扫描过的扇形的面积.
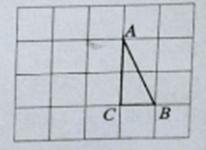
解析:
(1)

(2)AC旋转过程中扫过的扇形面积为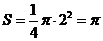
18(本小题满分8分)
“中国梦”关乎每个人的幸福生活,为进一步感知我们身边的幸福,展现成都人追梦的风采,我市某校开展了以”梦想中国”为主题的摄影大赛,要求参赛学生每人交一件作品,现将参赛的50件作品的成绩(单位:分)进行如下统计如下:

请根据上表提供的信息,解答下列问题:
(1)表中x的值为_______,y的值为______________;
(2)将本次参赛作品获得A等级的学生一次用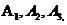 …表示,现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生
…表示,现该校决定从本次参赛作品获得A等级的学生中,随机抽取两名学生谈谈他们的参赛体会,请用树状图或列表法求恰好抽到学生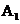 和
和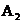 的概率。
的概率。
解析:
(1)x=4 ,y=0.7
(2)总共有4人获得A,设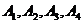 用列表法知所有抽取可能组合为:
用列表法知所有抽取可能组合为: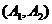
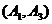 ,
,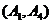 ,
,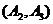 ,
,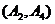 ,
,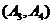 抽到
抽到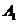 和
和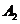 的概率为
的概率为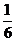
19.(本小题满分10分)
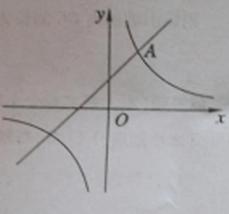
如图,一次函数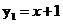 的图像与反比例函数
的图像与反比例函数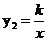 (k为常数,且
(k为常数,且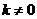 )的图像都经过点A(m,2).
)的图像都经过点A(m,2).
(1)求点A的坐标及反比例函数的表达式;
(2)结合图像直接比较:当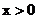 时,
时,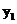 与
与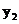 的大小。
的大小。
解析:
(1)点A(m,2)在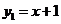 以及
以及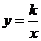 上
上
则代入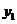 有m+1=2⇒m=1 ∴点A为(1,2)
有m+1=2⇒m=1 ∴点A为(1,2)
将点A代入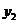 有
有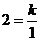 ⇒k=2 ∴
⇒k=2 ∴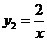
(2)结合图像知
ⅰ)当0<x<1时,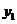 在
在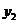 的下方 ∴
的下方 ∴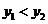
ⅱ)当x=1时,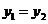
ⅲ)当x>1时,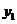 在
在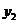 的上方 ∴
的上方 ∴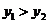
20.(本小题满分10分)
如图,点B在线段AC上,点D,E在AC同侧,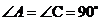 ,
,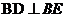 ,AD=BC.
,AD=BC.
(1)求证:AC=AD+CE;
(2)若AD=3,CE=5,点P为线段AB上的动点,连接DP,作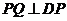 ,交直线BE于点Q.
,交直线BE于点Q.
i)若点P与A,B两点不重合,求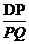 的值;
的值;
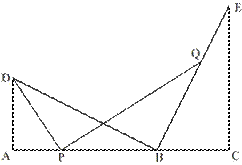
ii)当点P从A点运动到AC的中点时,求线段DQ的中点所经过的路径(线段)长。(直接写出结果,不必写出解答 )。
解析:
(1)证明:∠A=∠C=90°DB⊥BE
有∠ADB+∠ABD=90°以及∠ABD+∠EBC=90°
∴∠ADB=∠EBC 又AD=BC
∴Rt△ADB≌Rt△EBC ⇒AB=EC
∴AC=AB+BC=EC+AD
(2)
ⅰ)连结DQ, ∠DPQ=∠DBQ=90°, ∴D,PB,Q四点共圆.
且DQ为该圆直径,那么就有∠DQP=∠DBP
∴Rt△DPQ∽Rt△DAB
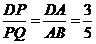
ⅱ)P到AC中点时,AP=4,AD=3,由勾股定理得DP=5
由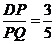 ⇒
⇒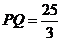 .
.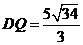 又
又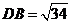
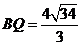 ∴
∴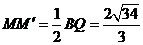
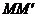 即为中点运动轨迹。
即为中点运动轨迹。
B卷(共50分)
一、填空题(本大题共5个小题,每小题4分,共20分,答案写在答题卡上)
21.已知点(3,5)在直线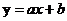 (a,b为常数,且
(a,b为常数,且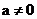 )上,则
)上,则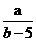 的值为__________.
的值为__________.
答案: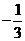
解析:将(3,5)代入直线方程有3a+b=5 ∴b-5=-3a
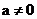 ,∴b≠5 ∴
,∴b≠5 ∴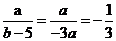
22.若正整数n使得在计算n+(n+1)+(n+2)的过程中,个数位上均不产生进为现象,则称n为“本位数”,例如2和30是 “本位数”,而5和91不是“本位数”.现从所有大于0且小于100的“本位数”中,随机抽取一个数,抽到偶数的概率为____.
答案: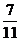
解析:各位数上均不进位,那么n的个位数上只能是0,1,2,否则就要在个位上发生进位,在大于0小于100的数中,一位数的本位数有1,2.两位数中十位数字不能不超过3,否则向百位进位,所以有3×3=9个,分别为10,11,12,20,21,22,30,31,32,其中偶数有7个,共有11个本位数,所以其概率为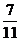
23.若关于t的不等式组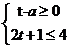 ,恰有三个整数解,则关于x的一次函数
,恰有三个整数解,则关于x的一次函数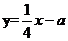 的图像与反比例函数
的图像与反比例函数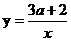 的图像的公共点的个数位______.
的图像的公共点的个数位______.
答案:2
解析:不等式组的解为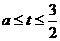 ,恰有3个整数解⇒-2<a≤-1
,恰有3个整数解⇒-2<a≤-1
联立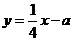 和
和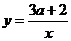 ⇒
⇒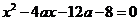
△=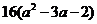 当-2<a≤-1时
当-2<a≤-1时
△=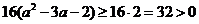
∴该方程有两个解,即两图像公共点个数为2
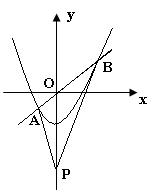
24.在平面直角坐标系xOy中,直线y=kx(k为常数)与抛物线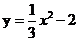 交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:
交于A,B两点,且A点在y轴左侧,P点坐标为(0,-4),连接PA,PB.有以下说法:
① 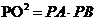 ;
;
② 当k>0时,(PA+AO)(PB-BO)的值随k的增大而增大;
③ 当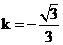 时,
时,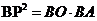 ;
;
④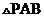 面积的最小值为
面积的最小值为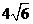 .
.
其中正确的是___________.(写出所有正确说法的序号)
答案:③④
解析:如图,无法证明△PAO∽△POB,故①不一定成立;对于②,取特殊值估算,知(PA+AO)(PB-BO)的值不是随k的增大而增大,也错。对于③,当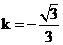 时,联立方程组:
时,联立方程组: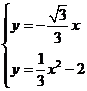 ,得A(-2
,得A(-2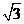 ,2),B(
,2),B(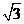 ,-1),BP2=12,BO•BA=2×6=12,故③正确;对于④,设
,-1),BP2=12,BO•BA=2×6=12,故③正确;对于④,设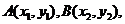 则三角形PAB的面积为:S=
则三角形PAB的面积为:S=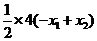 =
=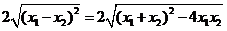
又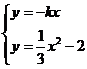 ,得
,得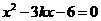 ,所以,
,所以,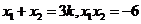 ,因此,
,因此,
S=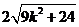 ,当k=0时,S最小为
,当k=0时,S最小为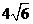 ,故
,故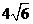 正确。
正确。
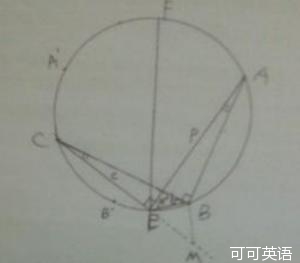
25如图,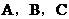 ,为⊙
,为⊙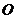 上相邻的三个
上相邻的三个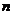 等分点,弧
等分点,弧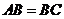 ,点
,点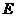 在弧
在弧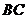 上,
上,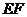 为⊙
为⊙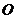 的直径,将⊙
的直径,将⊙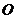 沿
沿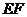 折叠,使点
折叠,使点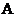 与
与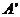 重合,连接
重合,连接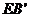 ,
,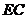 ,
,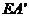 .设
.设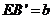 ,
,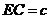 ,
,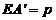 .先探究
.先探究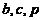 三者的数量关系:发现当
三者的数量关系:发现当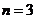 时,
时, 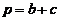 .请继续探究
.请继续探究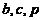 三者的数量关系:
三者的数量关系:
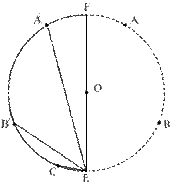 当
当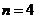 时,
时,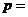 _______;当
_______;当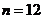 时,
时,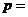 _______.
_______.
(参考数据: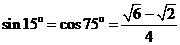 ,
,
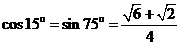 )
)
答案: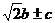 ;
;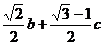 或
或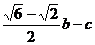
解析:
二、解答题(本大题共3个小题,共30分.答案写在答题卡上)
26.某物体从P点运动到Q点所用时间为7秒,其运动速度V(米/秒)关于时间t(秒)的函数关系如图所示。某学习小组经过探究发现:该物体前3秒运动的路程在数值上等于矩形AODB的面积。有物理学知识还可知:该物体前n(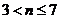 )秒运动的路程在数值上等于矩形AODB的面积与梯形BDMN的面积之和。
)秒运动的路程在数值上等于矩形AODB的面积与梯形BDMN的面积之和。
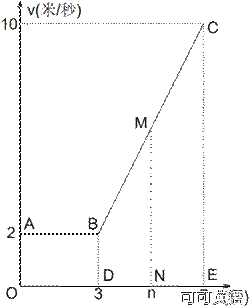
根据以上信息,完成下列问题:
(1)当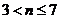 时,用含t的代数式表示;
时,用含t的代数式表示;
(2)分别求该物体在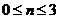 和
和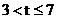 时,运动的路程,(米)关于时间t(秒)的函数关系式;并求该物体从P点运动到Q点总路程的
时,运动的路程,(米)关于时间t(秒)的函数关系式;并求该物体从P点运动到Q点总路程的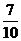 时所用的时间。
时所用的时间。
解析:
(1)点B(3,2) 点C(7,10),设V=kt+b代入有
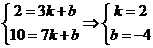
∴V=2t-4 (3<t≤7)
(2)
ⅰ)当0≤t≤3时,V=2m/s S=vt=2t
ⅱ) 当3<t≤7时
S=2×3+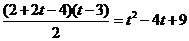
t=7时,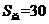
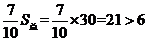
∴令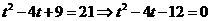
⇒(t-6)(t+2)=0⇒t=6
∴运动到总路程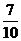 所用的时间为6s
所用的时间为6s
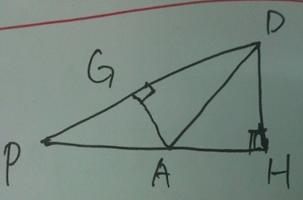
27.如图,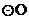 的半径r=25,四边形ABCD内接于
的半径r=25,四边形ABCD内接于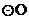 ,
,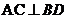 于点H,P为CA延长线上的一点,且
于点H,P为CA延长线上的一点,且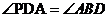 。
。
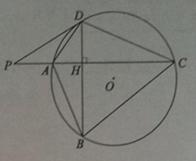
(1)试判断PD与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若 ,
,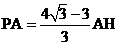 ,求BD的长;
,求BD的长;
(3)在(2)的条件下,求四边形ABCD的面积。
解析:
(1)PD与⊙O相切,∠ABD=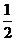 ∠AOD
∠AOD
∠ADO+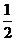 ∠ADO=90° ∴∠ADO+∠PDA=90°
∠ADO=90° ∴∠ADO+∠PDA=90°
∴PD⊥DO即PD与⊙O相切
(2)设AH=x,AC⊥BD ∠PHD=90°
由tan∠ADB=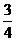 知DH=
知DH=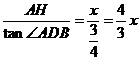
又PA=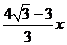 ∴PH=PA+AH=
∴PH=PA+AH=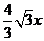
∴PD=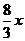 =2DH ⇒∠PDH=60°
=2DH ⇒∠PDH=60°
因为PD为⊙O切线,由割线弦定理知∠DCB=∠PDH=60°
∴∠DOB=120° BD=2R·sin60°=2×25×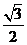 =25
=25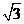
(3)过A作AG⊥PD
∵PA=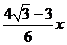 ∠DPH=30°
∠DPH=30°
∴GA=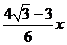 PG=
PG=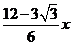
∴tan∠PDA=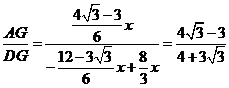
∴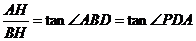
∴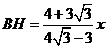
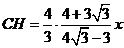
∴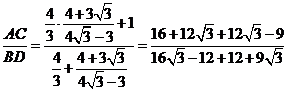
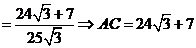
又AC⊥BD ∴S=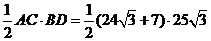
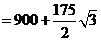
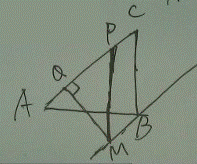
28.在平面直角坐标系中,已知抛物线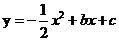 (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(4,3),直角顶点B在第四象限。
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(4,3),直角顶点B在第四象限。
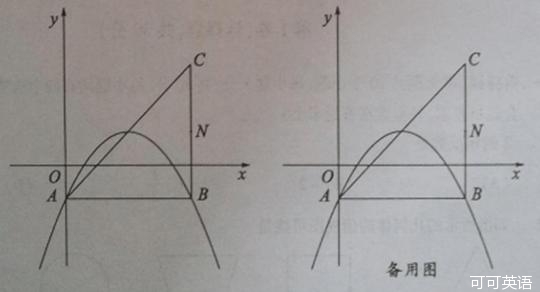
(1)如图,若该抛物线过A,B两点,求抛物线的函数表达式;
(2)平(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
i)若点M在直线AC下方,且为平移前(1)中的抛物线上点,当以M,P,Q三点为顶点的三角形是等腰三角形时,求出所有符合条件的M的坐标;
ii)取BC的中点N,连接NP,BQ。试探究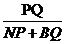 是否存在最大值?若存在,求出该最大值;所不存在,请说明理由。
是否存在最大值?若存在,求出该最大值;所不存在,请说明理由。
解析:
(1)A(0,-1) C(4,3) 则|AC|=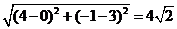
ABC为等腰直角三角形 ∴AB=BC=4
∴B点(4,-1)将A,B代入抛物线方程有
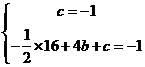 ⇒
⇒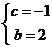
∴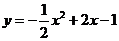
(2)当顶点P在直线AC上滑动时,平移后抛物线与AC另一交点Q就是A点沿直线AC滑动同样的单位。下面给予证明:
原抛物线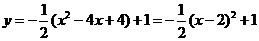 顶点P为(2,1)
顶点P为(2,1)
设平移后顶点P为(a,a-1),则平移后抛物线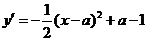 联立y=x-1(直线AC方程)
联立y=x-1(直线AC方程)
得Q点为(a-2,a-3)
∴|PQ|=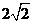 即实际上是线段AP在直线AC上的滑动.
即实际上是线段AP在直线AC上的滑动.
ⅰ)点M在直线AC下方,且M,P,Q构成等腰直角三角形,那么先考虑使MP,Q构成等腰直角三角形的M点的轨迹,再求其轨迹与抛物线的交点以确定M点.
①若∠M为直角,则M点轨迹即为AC下方距AC为MH且与AC平行的直线l
又知|PQ|=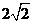 ,则|MH|=
,则|MH|=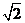 |PM|=2
|PM|=2
直线l即为AC向下平移|PM|=2个单位 L:y=x-3 联立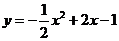
得x=1±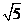
M点为(1+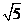 ,
,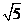 -2)或(1-
-2)或(1-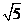 ,-
,-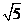 -2)
-2)
②若∠P=或∠Q为直角,即PQ为直角边,MQ⊥PQ且,MQ=PQ=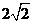
或MP⊥PQ,且MP=PQ=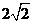 ,∴M点轨迹是AC下方距AC为
,∴M点轨迹是AC下方距AC为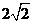 且与AC平行直线L
且与AC平行直线L
直线L即为AC向下平移|MP|=4个单位
L:y=x-5 联立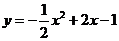 得x=4或x=-2
得x=4或x=-2
∴M点为(4,-1)或(-2,-7)
综上所有符合条件的点M为(1+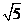 ,
,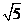 -2)(4,-1);(1-
-2)(4,-1);(1-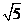 ,-
,-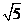 -2),(-2,-7)
-2),(-2,-7)
ⅱ)知PQ=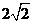
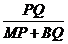 有最大值,即NP+BQ有最小值
有最大值,即NP+BQ有最小值
如下图,取AB中点M,连结QM,NM,知N为中点
∴MN为AC边中位线,∴MN∥AC且MN=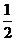 AC=
AC=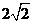 =PQ
=PQ
∴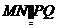 ∴MNPQ为平行四边形
∴MNPQ为平行四边形
即PN=QM ∴QB+PN=BQ+MQ
此时,作B点关于AC对称的点B′,连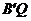 ,
,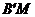
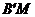 交AC于点H,易知
交AC于点H,易知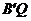 =BQ
=BQ
∴BQ+PN=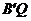 +MQ≥
+MQ≥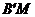 (三角形两边之和大于第三边)
(三角形两边之和大于第三边)
仅当Q与H重合时,取等号
即BQ+PN最小值存在 且最小值为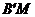
连结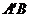 知
知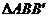 为等腰直角三角形。
为等腰直角三角形。
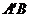 =4,AM=
=4,AM=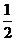 AB=2 ∴由勾股定理得
AB=2 ∴由勾股定理得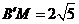
∴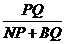 最大值存在,且最大值为
最大值存在,且最大值为