第Ⅰ卷（选择题，共36分）

一、选择题（本大题共12小题，每小题3分，共36分）

1． 5的相反数是（　　）

A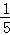． B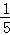． ﹣ C． 5 D． ﹣5

2． 中国航母辽宁舰是中国人民海军第一艘可以搭载固定翼飞机的航空母舰，满载排水量为67500吨，这个数据用科学记数法表示为（　　）

A． 6.75×104吨 B． 6.75×103吨 C． 6.75×105吨 D． 6.75×10﹣4吨

考点：科学记数法—表示较大的数．

3． 某市5月份连续五天的日最高气温（单位：℃）分别为：33，30，30，32，35．则这组数据的中位数和平均数分别是（　　）

A． 32，33 B． 30，32 C． 30，31 D． 32，32

【答案】D．

【解析】

4． 下列运算正确的是（　　）

A． 2a﹣a=1 B． （a﹣1）2=a2﹣1 C． a•a2=a3 D． （2a）2=2a2

考点：1.完全平方公式2.同底数幂的乘法3.幂的乘方与积的乘方．

5． 下列图形中，既是轴对称图形又是中心对称图形的是（　　）

A． 正三角形 B． 平行四边形 C． 矩形 D． 正五边形

6． 分式方程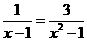的解是（　　）

A． x=﹣1 B． x=1 C． x=2 D． 无解

【答案】C．

【解析】

试题分析：去分母得：x+1=3，

解得：x=2，

经检验x=2是分式方程的解．

故选C．

考点：解分式方程．

7． 下列命题中，属于真命题的是（　　）

A． 同位角相等 B． 正比例函数是一次函数

C． 平分弦的直径垂直于弦 D． 对角线相等的四边形是矩形

考点：命题与定理．

8． 若关于x的一元二次方程x2+bx+c=0的两个实数根分别为x1=﹣2，x2=4，则b+c的值是（　　）

　A． ﹣10 B． 10 C． ﹣6 D． ﹣1

考点：根与系数的关系．

9． 如图，AB是⊙O的直径，，∠COD=34°，则∠AEO的度数是（　　）

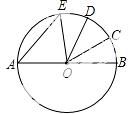
A． 51° B． 56° C． 68° D． 78°

考点：圆心角、弧、弦的关系．

10． 如图，在平面直角坐标系中，反比例函数y1=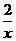的图象与一次函数y2=kx=b的图象交于A、B两点．若y1＜y2，则x的取值范围是（　　）

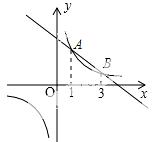
A． 1＜x＜3 B． x＜0或1＜x＜3 C． 0＜x＜1 D． x＞3或0＜x＜1

11． 如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，AD是∠BAC的平分线．若P，Q分别是AD和AC上的动点，则PC+PQ的最小值是（　　）

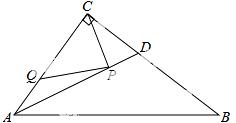
A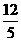． B． 4 C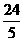． D． 5

【答案】C．

【解析】

试题分析：如图，过点C作CM⊥AB交AB于点M，交AD于点P，过点P作PQ⊥AC于点Q，

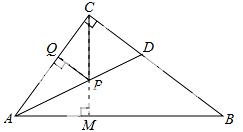
∵AD是∠BAC的平分线．

考点：轴对称-最短路线问题．

12． 已知二次函数y=ax2+bx+c（a≠0）的图象如图，分析下列四个结论：

①abc＜0；②b2﹣4ac＞0；③3a+c＞0；④（a+c）2＜b2，

其中正确的结论有（　　）

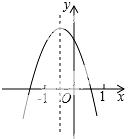
A． 1个 B． 2个 C． 3个 D． 4个

【答案】B．

【解析】

故选B．

考点：二次函数图象与系数的关系．

第Ⅱ卷（非选择题，共84分）

二、填空题（本大题共6小题，每小题3分，共18分）

13． 计算：﹣9+3=_________．

【答案】﹣6．

【解析】

试题分析：原式利用异号两数相加的法则计算可得：﹣9+3=﹣（9﹣3）=﹣6．

故答案是﹣6．

考点：有理数的加法．

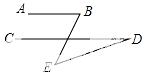
14． 如图所示，AB∥CD，∠D=27°，∠E=36°，则∠ABE的度数是____．

15． 一组数据1，3，0，4的方差是____．

【答案】2.5．

【解析】

试题分析：这组数据的平均数是：（1+3+0+4）÷4=2，

方差=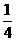 [（1﹣2）2+（3﹣2）2+（0﹣2）2+（4﹣2）2]=2.5．

故答案是2.5．

考点：方差．

16． 如图，在等腰梯形ABCD中，AD∥BC，AB=DC，AC⊥BD．若AD=4，BC=6，则梯形ABCD的面积是　．

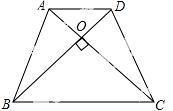
【答案】25．

【解析】

试题分析：过点D作DE∥AC，交BC的延长线于点E，

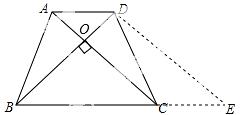
∵AD∥BC，

∴四边形ACED是平行四边形，

∴AC=DE，CE=AD=4，

考点：等腰梯形的性质．

17． 如图，在菱形ABCD中，AB=2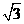，∠C=120°，以点C为圆心的与AB，AD分别相切于点G，H，与BC，CD分别相交于点E，F．若用扇形CEF作一个圆锥的侧面，则这个圆锥的高是____．

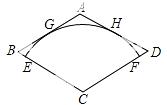
【答案】2．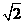

【解析】

试题分析：连接CG，

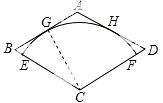
故答案是2．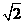

考点：1.切线的性质2.菱形的性质3.圆锥的计算．

18． 已知点A1（a1，a2），A2（a2，a3），A3（a3，a4）…，An（an，an+1）（n为正整数）都在一次函数y=x+3的图象上．若a1=2，则a2014=____．

三、解答题（本大题共8小题，满分66分，解答用写出文字说明，证明过程或演算步骤）

19．（10分） （1）计算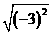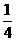：﹣（）﹣1+（π﹣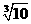）0﹣（﹣1）10；

（2）已知|a+1|+（b﹣3）2=0，求代数式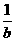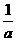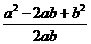（﹣）÷的值．

考点：1.实数的运算2.零指数幂3.负整数指数幂4.分式的化简及求值．

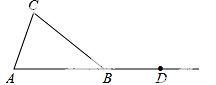
20．（5分） 如图，在△ABC中，AB=BC，点点D在AB的延长线上．

（1）利用尺规按下列要求作图，并在图中标明相应的字母（保留作图痕迹，不写作法）．

①作∠CBD的平分线BM；

②作边BC上的中线AE，并延长AE交BM于点F．

（2）由（1）得：BF与边AC的位置关系是___________．

【答案】（1）图形见解析；（2）BF∥AC．

【解析】

试题分析：（1）①利用角平分线的作法得出BM；

②首先作出BC的垂直平分线，进而得出BC的中点，进而得出边BC上的中线AE；

（2）利用三角形的外角的性质以及等腰三角形的性质得出即可．

试题解析：（1）①如图所示：BM即为所求；

②如图所示：AF即为所求；

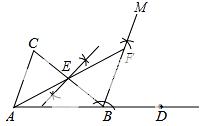
（2）∵AB=BC，

∴∠CAB=∠C，

∵∠C+∠CAB=∠CBD，∠CBM=∠MBD，

∴∠C=∠CBM，

∴BF∥AC．

考点：作图—复杂作图．

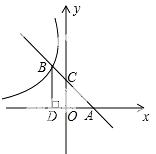
21．（6分） 如图所示，直线AB与x轴交于点A，与y轴交于点C（0，2），且与反比例函数y=﹣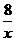的图象在第二象限内交于点B，过点B作BD⊥x轴于点D，OD=2．

（1）求直线AB的解析式；

（2）若点P是线段BD上一点，且△PBC的面积等于3，求点P的坐标．

，

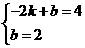解得，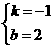

∴直线AB的解析式为y=﹣x+2；

（2）∵OD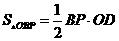=3，=3，

∴BP=3，

PD=BD﹣BP=4﹣3=1，

∴P点坐标是（﹣2，1）．

考点：反比例函数与一次函数的交点问题．

22．（8分） 某学校举行“社会主义核心价值观”知识比赛活动，全体学生都参加比赛，学校对参赛学生均给与表彰，并设置一、二、三等奖和纪念奖共四个奖项，赛后将获奖情况绘制成如下所示的两幅不完整的统计图，请根据图中所给的信息，解答下列问题：

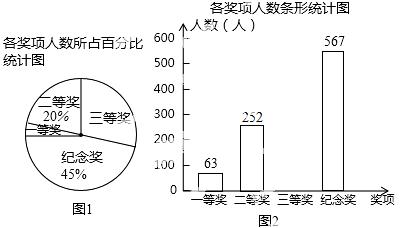
（1）该校共有　名学生；

（2）在图①中，“三等奖”随对应扇形的圆心角度数是　；

（3）将图②补充完整；

（4）从该校参加本次比赛活动的学生中随机抽查一名．求抽到获得一等奖的学生的概率．

【答案】（1）1260；

（2）108°；

（3）图形见解析；

（4）抽到获得一等奖的学生的概率为5%．

【解析】

（3）三等奖的人数为：1260×（1﹣20%﹣5%﹣45%）=378人，如图2，

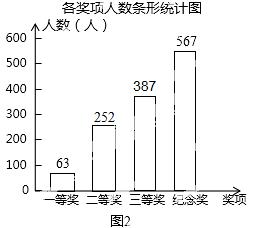
（4）抽到获得一等奖的学生的概率为：63÷1260=5%．

考点：1.条形统计图2.扇形统计图3.概率公式．

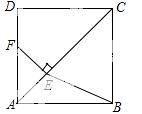
23．（7分） 如图，在正方形ABCD中，点E是对角线AC上一点，且CE=CD，过点E作EF⊥AC交AD于点F，连接BE．

（1）求证：DF=AE；

（2）当AB=2时，求BE2的值．

【答案】（1）证明见解析；

（2）BE2=8﹣4．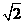

【解析】

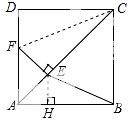
在Rt△CDF和Rt△CEF中，

，

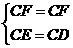则△AEH是等腰直角三角形，

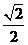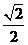∴AE=AH=AE=×（2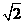﹣2）=2﹣，

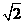∴BH=2﹣（2﹣）=，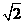

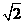在Rt△BEH中，BE2=BH2+EH2=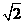（）2+（2﹣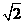）2=8﹣4．

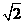考点：1.正方形的性质2.角平分线的性质3.勾股定理．

24．（9分） 在开展“美丽广西，清洁乡村”的活动中某乡镇计划购买A、B两种树苗共100棵，已知A种树苗每棵30元，B种树苗每棵90元．

（1）设购买A种树苗x棵，购买A、B两种树苗的总费用为y元，请你写出y与x之间的函数关系式（不要求写出自变量x的取值范围）；

（2）如果购买A、B两种树苗的总费用不超过7560元，且B种树苗的棵树不少于A种树苗棵树的3倍，那么有哪几种购买树苗的方案？

（3）从节约开支的角度考虑，你认为采用哪种方案更合算？

，

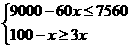考点：1.一次函数的应用2.一元一次不等式组的应用．

25．（10分） 如图，AB是大半圆O的直径，AO是小半圆M的直径，点P是大半圆O上一点，PA与小半圆M交于点C，过点C作CD⊥OP于点D．

（1）求证：CD是小半圆M的切线；

（2）若AB=8，点P在大半圆O上运动（点P不与A，B两点重合），设PD=x，CD2=y．

①求y与x之间的函数关系式，并写出自变量x的取值范围；

②当y=3时，求P，M两点之间的距离．

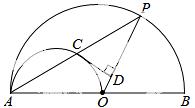
变量x的取值范围为0＜x＜4；

②当y=3时，得到﹣x2+4x=3，求出x．根据x的值可求出CD、PD的值，从而求出∠CPD，运用勾股定理等知识就可求出P，M两点之间的距离．

试题解析：（1）连接CO、CM，如图1所示．

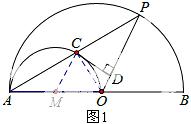
∵AO是小半圆M的直径，

∴∠ACO=90°即CO⊥AP．

∵OA=OP，

∴AC=PC．

∵AM=OM，

∴CM∥PO．

当点P与点A重合时，x=0；当点P与点B重合时，x=4；

∵点P在大半圆O上运动（点P不与A，B两点重合），

∴0＜x＜4．

∴y与x之间的函数关系式为y=﹣x2+4x，

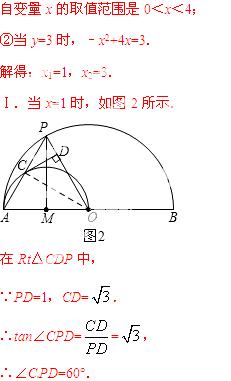
∵OA=OP，

∴△OAP是等边三角形．

∵AM=OM，

∴PM⊥AO．

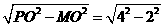∴PM==2．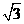

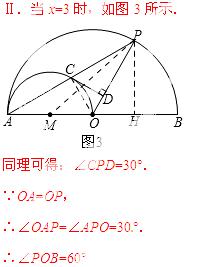
过点P作PH⊥AB，垂足为H，连接PM，如图3所示．

∵sin∠POH=，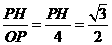

∴PH=2．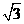

同理：OH=2．

在Rt△MHP中，

∵MH=4，PH=2，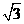

∴PM=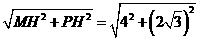=2．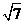

综上所述：当y=3时，P，M两点之间的距离为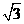2或2．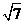

考点：圆的综合题．

26．（11分） 如图，抛物线y=ax2+bx﹣3a（a≠0）与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，2），连接BC．

（1）求该抛物线的解析式和对称轴，并写出线段BC的中点坐标；

（2）将线段BC先向左平移2个单位长度，在向下平移m个单位长度，使点C的对应点C1恰好落在该抛物线上，求此时点C1的坐标和m的值；

（3）若点P是该抛物线上的动点，点Q是该抛物线对称轴上的动点，当以P，Q，B，C四点为顶点的四边形是平行四边形时，求此时点P的坐标．

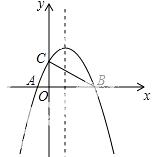
线的解析式和对称轴，再求出点B的坐标，根据中点坐标公式求出线段BC的中点坐标即可；

（2）根据平移的性质可知，点C的对应点C1的横坐标为﹣2，再代入抛物线可求点C1的坐标，进一步得到m的值；

（3）B、C为定点，可分BC为平行四边形的一边及对角线两种情况探讨得到点P的坐标．

∴点C1的横坐标为﹣2，

当x=﹣2时，y=﹣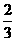×（﹣2）2+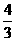×（﹣2）+2=﹣，

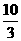∴点C1的坐标为（﹣2，﹣），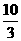

m=2﹣（﹣）=；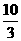

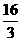（3）①若BC为平行四边形的一边，

∵BC的横坐标的差为3，

∵点Q的横坐标为1，

∴P的横坐标为4或﹣2，

∵P在抛物线上，

∴P的纵坐标为﹣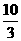，