(单词翻译:单击)
中考数学真题
2014年湖北省孝感市中考数学真题附答案
温馨提示:
1.答题前,考生务必将自己所在县(市、区)、学校、姓名、考号填写在试卷上指定的位置.
2.选择题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑;非选择题的答案必须写在答题卡的指定位置,在本卷上答题无效.
3.本试卷满分120分,考试时间120分钟.
一、精心选一选,相信自己的判断!(本大题共12小题,每小题3分,共36分.在每小题给出的四个选项中只有一项是符合题目要求的,不涂、错涂或涂的代号超过一个,一律得0分)
 1.下列各数中,最大的数是
1.下列各数中,最大的数是
A. B.
B. C.
C.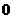 D.
D.
2.如图是某个几何体的三视图,则该几何体的形状是
A.长方体 B.圆锥 C.圆柱 D.三棱柱
3.下列二次根式中,不能与 合并的是
合并的是

A.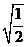 B.
B.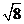 C.
C. D.
D.
4.如图,直线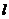 1//
1//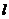 2,
2,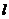 3⊥
3⊥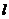 4,∠1=44°,那么∠2的度数为
4,∠1=44°,那么∠2的度数为
| (第4题图) |
A.46° B.44° C.36° D.22°
5.已知 是二元一次方程组
是二元一次方程组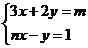 的解,则
的解,则 的值是
的值是
A. B.
B.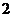 C.
C. D.
D.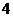
6.分式方程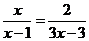 的解为
的解为
A. B.
B. C.
C.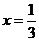 D.
D.
居民(户) | 1 | 3 | 2 | 4 |
月用电量(度/户) | 40 | 50 | 55 | 60 |
7.为了解某社区居民的用电情况,随机对该社区10户居民进行了调查,下表是这10户居民2014年4月份用电量的调查结果:那么关于这10户居民月用电量(单位:度),下列说法错误的是
A.中位数是55 B.众数是60 C.方差是29 D.平均数是54

8.如图,在 ABCD中,对角线AC、BD相交成的锐角为 ,
, 若
若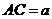 ,
,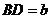 ,则 ABCD的面积是
,则 ABCD的面积是
A. B.
B.
C. D.
D.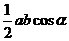

9.如图,正方形 的两边
的两边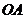 、
、 分别在
分别在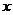 轴、
轴、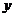 轴上,点
轴上,点 (5,3)在边
(5,3)在边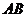 上,以
上,以 为中心,把△
为中心,把△ 旋转90°,则旋转后点
旋转90°,则旋转后点 的对应点
的对应点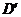 的坐标是
的坐标是
A.(2,10) B.(-2,0)
C.(2,10)或(-2,0) D.(10,2)或(-2,0)
10.如图,在半径为6 的⊙
的⊙ 中,点
中,点 是劣弧
是劣弧 的中点,点
的中点,点 是优弧
是优弧 上一点,且
上一点,且 ,下列四个结论:①
,下列四个结论:①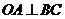 ;②
;② ;③
;③ ;④四边形
;④四边形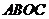 是菱形.其中正确结论的序号是
是菱形.其中正确结论的序号是
A.①③ B.①②③④ C.②③④ D.①③④
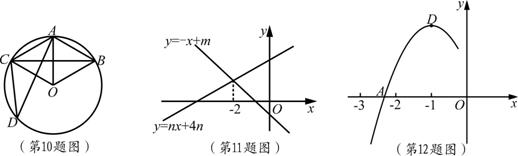
11.如图,直线 与
与 (
(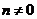 )的交点的横坐标为
)的交点的横坐标为 ,则关于x的不等式
,则关于x的不等式 的整数解为
的整数解为
A. B.
B. C.
C. D.
D.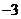
12.抛物线 的顶点为
的顶点为 ,与
,与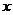 轴的一个交点
轴的一个交点 在点
在点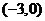 和
和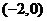 之间,其部分图象如图所示,则以下结论:①
之间,其部分图象如图所示,则以下结论:①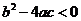 ;②
;② ;
;
③ ;④方程
;④方程 有两个相等的实数根,其中正确结论的个
有两个相等的实数根,其中正确结论的个 数为
数为
A.1个  B.2个
B.2个  C.3个 D.4个
C.3个 D.4个
二、细心填一填,试试自己的身手!(本大题共6小题,每小题3分,共18分.请将结果直接填写在答题卡相应位置上)
13.函数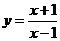 的自变量
的自变量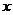 的取值范围是 ☆ .
的取值范围是 ☆ .
14.下列事件:①随意翻到一本书的某页,这页的页码是奇数;②测得某天的最高气温是100℃;③掷一次骰子,向上一面的数字是2;④度量四边形的内角和,结果是360°.其中是随机事件的是 ☆ .(填序号)
15.若 ,则代数式
,则代数式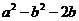 的值为 ☆ .
的值为 ☆ .
16.如图,已知矩形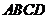 ,把矩形沿直线
,把矩形沿直线 折叠,点
折叠,点 落在点
落在点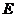 处,连接
处,连接 、
、 ,若△
,若△ 是等边三角形,则
是等边三角形,则 = ☆ .
= ☆ .

17.如图,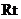 △
△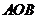 的一条直角边
的一条直角边 在
在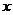 轴上,双曲线
轴上,双曲线 经过斜边
经过斜边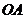 的中点
的中点 ,与另一直角边交于点
,与另一直角边交于点 ,若
,若 =9,则
=9,则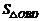 的值为 ☆ .
的值为 ☆ .
18.正方形 ,
,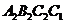 ,
, ,…按如图所示的方式放置.点
,…按如图所示的方式放置.点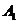 ,
, ,
,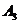 ,…和点
,…和点 ,
,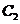 ,
, ,…分别在直线
,…分别在直线 和
和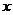 轴上,则点
轴上,则点 的坐标是 ☆ .
的坐标是 ☆ .

三 、用心做一做,显显自己的能力!(本大题共7小题,满分66分.解答写在答题卡上)
、用心做一做,显显自己的能力!(本大题共7小题,满分66分.解答写在答题卡上)
19.(本题满分6分)
计算: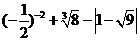
20.(本题满分8分)
如图,在Rt△ 中,∠
中,∠ =90°.
=90°.
(1)先作∠ 的平分线交
的平分线交 边于点
边于点 ,再以点
,再以点 为圆心,
为圆心, 为半径作⊙
为半径作⊙ (要求:尺规作图,保留作图痕迹,不写作法);(4分)
(要求:尺规作图,保留作图痕迹,不写作法);(4分)
(2)请你判断(1)中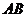 与⊙
与⊙ 的位置关系,并证明你的结论.(4分)
的位置关系,并证明你的结论.(4分)
 |
21.(本题满分10分)
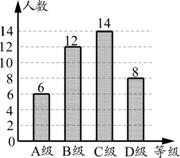
为了解中考体育科目训练情况,某县从全县九年级学生中随机抽取了部分学生进行了一次中考体育科目测试(把测试结果分为四个等级: 级:优秀;
级:优秀;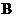 级:良好;
级:良好;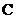 级:及格;
级:及格; 级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
级:不及格),并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
(1)本次抽样测试的学生人数是 ☆ ;(2分)
(2)图1中∠ 的度数是 ☆ ,并把图2条形统计图补充完整;(2分)
的度数是 ☆ ,并把图2条形统计图补充完整;(2分)
(3)该县九年级有学生3500名,如果全部参加这次中考体育科目测试,请估计不及格的人数为 ☆ ;(3分)
(4)测试老师想从4位同学(分别记为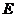 、
、 、
、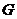 、
、 ,其中
,其中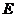 为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.(3分)
为小明)中随机选择两位同学了解平时训练情况,请用列表或画树形图的方法求出选中小明的概率.(3分)

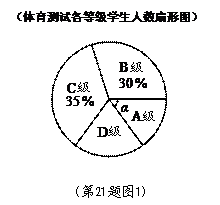 |
22.(本题满分10分)
已知关于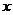 的方程
的方程 有两个不相等的实数根
有两个不相等的实数根 、
、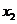 .
.
(1)求 的取值范围;(3分)
的取值范围;(3分)
(2)试说明 ,
, ;(3分)
;(3分)
(3)若抛物线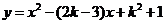 与
与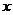 轴交于
轴交于 、
、 两点,点
两点,点 、点
、点 到原点的距离分别为
到原点的距离分别为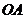 、
、 ,且
,且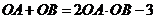 ,求
,求 的值.(4分)
的值.(4分)
23.(本题满分10分)
我市荸荠喜获丰收,某生产基地收获荸荠40吨.经市场调查,可采用批发、零售、加工销售三种销售方式,这三种销售方式每吨荸荠的利润如下表:
销售方式 | 批发 | 零售 | 加工销售 |
利润(百元/吨) | 12 | 22 | 30 |
设按计划全部售出后的总利润为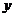 百元,其中批发量为
百元,其中批发量为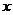 吨,且加工销售量为15吨.
吨,且加工销售量为15吨.
(1)求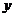 与
与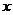 之间的函数关系式;(4分)
之间的函数关系式;(4分)
(2)若零售量不超过批发量的4倍,求该生产基地按计划全部售完荸荠后获得的最大利润.(6分)
24. (本题满分10分)
(本题满分10分)
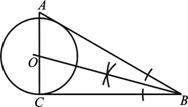
如图,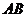 是⊙
是⊙ 的直径,点
的直径,点 是⊙
是⊙ 上一点
上一点 ,
,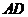 与过点
与过点 的切线垂直,垂足为点
的切线垂直,垂足为点 ,直线
,直线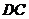 与
与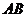 的延长线相交于点
的延长线相交于点 ,弦
,弦 平分∠
平分∠ ,交
,交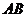 于点
于点 ,
, 连接
连接 .
.
(1)求证: 平分∠
平分∠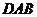 ;(3分)
;(3分)
(2)求证:△ 是等腰三角形;(3分)
是等腰三角形;(3分)
(3)若 ,
,
 ,求线段
,求线段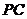 的长.(4分)
的长.(4分)
 |
25.(本题满分12分 )
)
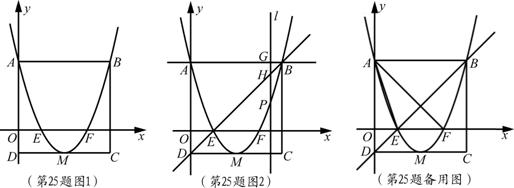
如图1,矩形 的边
的边 在
在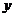 轴上,抛物线
轴上,抛物线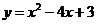 经过点
经过点 、点
、点 ,与
,与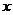 轴交于点
轴交于点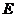 、点
、点 ,且其顶点
,且其顶点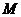 在
在 上.
上.
(1)请直接写出下列各点的坐标:
 ☆ ,
☆ , ☆ ,
☆ , ☆ ,
☆ , ☆ ;(4分)
☆ ;(4分)
(2)若点 是抛物线上一动点(点
是抛物线上一动点(点 不与点
不与点 、点
、点 重合),过点
重合),过点 作
作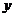 轴的平行线
轴的平行线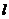 与直线
与直线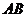 交于点
交于点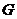 ,与直线
,与直线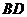 交于点
交于点 ,如图2.
,如图2.
①当线段 =
= 时,求点
时,求点 的坐标;(4分)
的坐标;(4分)
②当点 在直线
在直线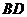 下方时,点
下方时,点 在直线
在直线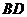 上,且满足△
上,且满足△ ∽△
∽△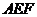 ,求△
,求△ 面积的最大值.(4分)
面积的最大值.(4分)
参考答案
孝感市2014年高中阶段学校招生考试
数学参考答案及评分说明
一、选择题
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | A | D | C | A | D | B | C | A | C | B | D | C |
二、填空题
13.x≠1; 14.①③; 15.1; 16. ; 17.6; 18.(63,32) .
; 17.6; 18.(63,32) .
三、解答题
19.解:原式= +2-
+2- ················· 2分
················· 2分
=4+2-2 ··················· 4分
 =4 ····················· 6分
=4 ····················· 6分
20.解:(1)如图:
·········· 4分
(2)AB与⊙O相切. ················· 6分
证明:作OD⊥AB于D,如图.
∵BO平分∠ABC,∠ACB=90°,OD⊥AB,
∴OD=OC,
| D |
| A |
∴AB与⊙O相切. ··················· 8分
 |
21.(1)40; …………………………………2分
…………………………………2分
| (第21题答案图) |
(2)54°,如图:… ………………………………4分
………………………………4分
(3)700; …………………………………7分
 (4)画树形图如下:
(4)画树形图如下:
·· 8分
∴P(选中小明)= . ············ 10分
. ············ 10分
22.解:(1)由题意可知: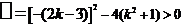 , ········· 1分
, ········· 1分
即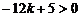 ········· 2分
········· 2分
∴ . ········ 3分
. ········ 3分
(2)∵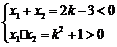 , ········ 5分
, ········ 5分
∴ . ········ 6分
. ········ 6分
( 3)依题意,不妨设A(x1,0),B(x2,0).
3)依题意,不妨设A(x1,0),B(x2,0).
∴ ,
,
 , ······· 8分
, ······· 8分
∵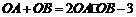 ,
,
∴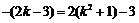 ,
,
解得k1=1,k2=-2. ········· 9分
∵ ,∴k=-2. ········ 10分
,∴k=-2. ········ 10分
23.解:(1)依题意可知零售量为(25-x)吨,则
y=12 x +22(25-x) +30×15 ··············· 2分
∴y =-10 x+1000 ················· 4分
(2)依题意有:
 , 解得:5≤x≤25. ······· 6分
, 解得:5≤x≤25. ······· 6分
∵-10<0,∴y随x的增大而减小. ········ 7分
∴当x=5时,y有最大值,且y最大=950(百元).
∴最大利润为950百元. ········ 10分
24. 解:(1)∵PD切⊙O于点C,∴OC⊥PD.··············· 1分
又AD⊥PD,∴OC∥AD.∴∠ACO=∠DAC.
又OC=OA,∴∠ACO=∠CAO,
∴∠DAC=∠CAO,即AC平分∠DAB.············· 3分
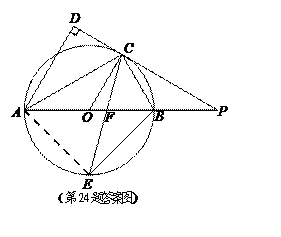
(2)∵AD⊥PD,∴∠DAC+∠ACD=90°.
又AB为⊙O的直径,∴∠ACB=90°.
∴∠PCB+∠ACD=90°,∴∠DAC=∠PCB.
又∠DAC= ∠CAO,∴∠CAO=∠PCB.…… 4分
∠CAO,∴∠CAO=∠PCB.…… 4分
∵CE平分∠ACB,∴∠ACF=∠BCF,
∴∠CAO+∠ACF=∠PCB+∠BCF,
∴∠PFC=∠PCF, …………… 5分
∴PC=PF,∴△PCF是等腰三 角形.…………… 6分
角形.…………… 6分
(3)连接AE.∵CE平分∠ACB,∴ ,∴
,∴ .
.
∵AB为⊙O的直径,∴∠AEB=90°.
在Rt△ABE中, . ········ 7分
. ········ 7分
∵∠PAC=∠PCB,∠P=∠P,∴△PAC∽△PCB,········ 8分
∴ .又tan∠ABC=
.又tan∠ABC= ,∴
,∴ ,∴
,∴ .
.
设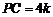 ,
, ,则在Rt△POC中,
,则在Rt△POC中,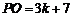 ,
, ,
,
∵ ,∴
,∴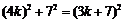 ,
,
∴k=6 (k=0不合题意,舍去).
∴ . ············ 10分
. ············ 10分
25.(1)A(0,3),B(4,3),C(4,-1),D(0,-1). ········· 4分
(2)①设直线BD的解析式为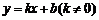 ,由于直线BD经过D(0,-1),B(4,3),
,由于直线BD经过D(0,-1),B(4,3),
∴ ,解得
,解得 ,∴直线BD的解析式为
,∴直线BD的解析式为 .·· 5分
.·· 5分
设点P的坐标为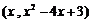 ,则点H
,则点H ,点G
,点G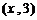 .
.
1°当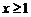 且x≠4时,点G在PH的延长线上,如图①.
且x≠4时,点G在PH的延长线上,如图①.
∵PH=2GH,∴ ,
,
∴ ,解得
,解得 ,
, .
.
当 时,点P,H,G重合于点B,舍去.
时,点P,H,G重合于点B,舍去.
∴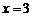 .∴此时点P的坐标为
.∴此时点P的坐标为 . ········ 6分
. ········ 6分
2°当 时,点G在PH的反向延长线上,如图②,PH=2GH不成立.………7分
时,点G在PH的反向延长线上,如图②,PH=2GH不成立.………7分
3°当 时,点G在线段PH上,如图③.
时,点G在线段PH上,如图③.
∵PH=2GH,∴ ,
,
∴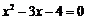 ,解得
,解得 ,
, (舍去),
(舍去),
∴ .此时点P的坐标为
.此时点P的坐标为 .
.
综上所述可知,点P的坐标为 或
或 . ······· 8分
. ······· 8分
 |
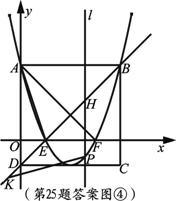
②如图④,令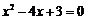 ,得
,得 ,
, ,∴E
,∴E ,F
,F ,∴E
,∴E F=2.
F=2.
 ∴
∴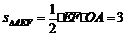 . ……………………9分
. ……………………9分
∵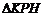 ∽
∽ ,∴
,∴ ,
,
∴ . …………11分
. …………11分
∵ ,
,
∴当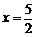 时,
时,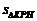 的最大值为
的最大值为 . …………12分
. …………12分
注意:1.按照评分标准分步评分,不得随意变更给分点;
2.上述各题的其它解法,只要思路清晰,解法正确,均应参照上述标准给予相应分数.


