(单词翻译:单击)
一、选择题(每小题4分,共48分)
1. 下列各数中,既不是正数也![]() 不是负数的是
不是负数的是
A. 0 B. -1 C. 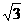 D. 2
D. 2
2. 宁波轨道交通1号线、2号线建设总投资253.7亿元,其中253.7亿用科学计数法表示为
A. 253.7×108 B. 25.37×109 C. 2.537×1010 D. 2.537×1011
3. 用矩形纸片折出直角的平分线,下列折法正确的是

4. 杨梅开始采摘啦!每筐杨梅以5千克为基准,超过的千克数记为正数,不足的千克数记为负数,记录如图,则这4筐杨梅的总质量是

A. 19.7千克 B. ![]() 19.9千克 C. 20.1千克 D. 20.3千克
19.9千克 C. 20.1千克 D. 20.3千克
5. 圆锥的母线长为4,底面半径为2,![]() 则此圆锥的侧面积是
则此圆锥的侧面积是
A.  B.
B.  C.
C.  D.
D. 
6. 菱形的两条对角线长分别是6和8,则此菱形的边长是
A. 10![]() B. 8 C. 6 D. 5
B. 8 C. 6 D. 5
7. 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为直角三角形的概率是
A. 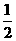 B.
B. 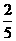 C.
C. 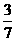 D.
D. 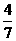
8. 如图,梯![]() 形ABCD中AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为
形ABCD中AD∥BC,∠B=∠ACD=90°,AB=2,DC=3,则△ABC与△DCA的面积比为
A. 2:3 B. 2:5 C. 4:9 D. 
9. 已知命题“关于 的一元二次方程
的一元二次方程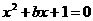 ,当
,当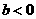 时必有实数解”,能说明这个命题是假命题的一个反例是
时必有实数解”,能说明这个命题是假命题的一个反例是
A.  B.
B. 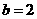 C.
C.  D.
D. 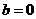
10. 如果一个多![]() 面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥。如图是一个四棱柱和一个六棱锥,它们各有12条棱,下列棱柱中和九棱锥的棱数相等的是
面体的一个面是多边形,其余各面是有一个公共顶点的三角形,那么这个多面体叫做棱锥。如图是一个四棱柱和一个六棱锥,它们各有12条棱,下列棱柱中和九棱锥的棱数相等的是
A. 五棱柱 B. 六棱柱 C. 七棱柱 D. 八棱柱
11. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是
A. 2.5 B. 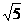 C.
C. 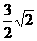 D. 2
D. 2

12. 已知点A( ,
,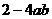 )在抛物线
)在抛物线 上,则点A关于抛物线对称轴的对称点坐标为
上,则点A关于抛物线对称轴的对称点坐标为
A. (-3,7) B. (-1,7) C. (-4,10) D. (0,10)
二、填空题(每小题4分,共24分)
13. -4的绝对值是_________
14. 方程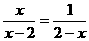 的根是
的根是 = _________
= _________
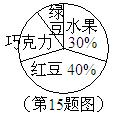
15. 某冷饮店一天售出各种口味雪糕数量的扇形统计图如图所示,其中售出红豆口味的雪糕200支,那么售出水果口味雪糕的数量是 _________ 支
16. 一个大正方形和四个全等的小正方形按图①、②两种方式摆放,则图②的大正方形中,未被小正 方形覆盖部分的面积是 _________(用
方形覆盖部分的面积是 _________(用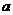 ,
, 的代数式表示)
的代数式表示)
17. 为解决停车难得问题,在如图一段长56米的路段开辟停车位,每个![]() 车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出 _________个这样的停车位(
车位是长5米、宽2.2米的矩形,矩形的边与路的边缘成45°角,那么这个路段最多可以划出 _________个这样的停车位(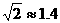 )
)
18. 如图,半径为6cm的⊙O中,C,D为直径AB的三等分点,点E,F分别在AB两侧的半圆上,∠BCE=∠BDF=60°,连结AE,BF,则图中 两个阴影部分的面积为 _________ cm2
两个阴影部分的面积为 _________ cm2

三、解答题(本题有8小题,共78分)
19.(本题6分)
(1)化简: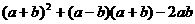 ;
;
(2)解不等式: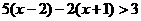
20.(本题8分)
作为宁波市政府民生实事之一的公共自行车建设工程已基本完成,某部门对今年4月份中的7天进行了公共自行车日租车辆的统计,结果如下:
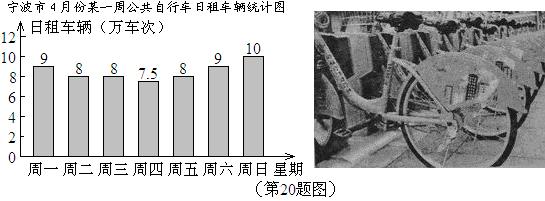
(1)求这7天租车辆的众数、中位数和平均数;
(2)用(1)中的平均数估计4月份(30天)共租车多少万车次?
(3)市政府在公共自行车建设项目中共投入9600万元,估计2014年共租车3200万车次,每车次平均收入租车费0.1元,求2014年租车费收入占总投入的百分率(精确到0.1%)
21.(本题8分)
如图,从A地到B地的公路需要经过C地,图中AC=10千米,∠CAB=25°,∠CBA=37°。因城市规划的需要,将在A,B两地之间修建一条笔直的公路。
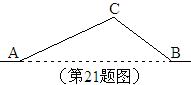
(1)求改直后的公路AB的长;
(2)问:公路改造后比原 来缩短了多少千米?
来缩短了多少千米?
(sin25°≈0.42,cos25°≈0.91,sin37°≈0.60,tan37°≈0.75)
22.(本题10分)
如图,点A,B分别在 轴,
轴, 轴上,点D在第一象限内,DC⊥
轴上,点D在第一象限内,DC⊥ 轴于点C,AO=CD=2,AB=DA=
轴于点C,AO=CD=2,AB=DA=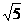 ,反比例函数
,反比例函数 的图象过CD的中点E。
的图象过CD的中点E。
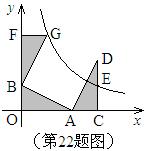
(1)求证:△AOB≌△DCA;
(2)求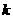 的值;
的值;
(3)△BFG和△DCA关于某点成中心对称,其中点F在 轴上,试判断点G是否在反比例函数的图象上,并说明理由。
轴上,试判断点G是否在反比例函数的图象上,并说明理由。
23.(本题10分)
如图,已知二次函数![]()
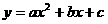 的图象过A(2,0),B(0,-1)和C(4,5)三点。
的图象过A(2,0),B(0,-1)和C(4,5)三点。
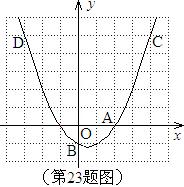
(1)求二次函数的解析式;
(2)设二次函数的图象与 轴的另一个交点为D,求点D的坐标;
轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线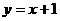 ,并写出当
,并写出当 在什么范围内时,一次函数的值大于二次函数的值。
在什么范围内时,一次函数的值大于二次函数的值。
24.(本题10分)
用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。
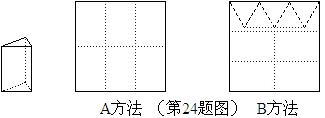
现有19张硬纸板,裁剪时 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
25.(本题12分)
课本作业题中有这样一道题:把一张顶角为36°的等腰三角形纸片剪两刀,分成3张小纸片,使每张小纸片都是等腰三角形,你能办到吗?请画示意图说明剪法。
我们有多种剪法,图1是其中的一种方法:
定义:如果两条线段将一个三角形分成3个等腰三角形,我们把这两条线段叫做这个三角形的三分线。
(1)请你在图2中用两种不同的方法画出顶角为45°的等腰三角形的三分线,并标注每个等腰三角形顶角的度数(若两种方法分![]() 得的三角形成3对全等三角形,则视为同一种);
得的三角形成3对全等三角形,则视为同一种);
(2)△ABC中,∠B=30°,AD和DE是△ABC的三分线,点D在BC边上,点E在AC边上,且AD=BD,DE=CE,设∠C=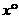 ,试画出示意图,并求出
,试画出示意图,并求出 所有可能的值;
所有可能的值;
(3)如图3,△ABC中,AC=2,BC=3,∠C=2∠![]() B,请画出△ABC的三分线,并求出三分线的长。
B,请画出△ABC的三分线,并求出三分线的长。
26.(本题14分)
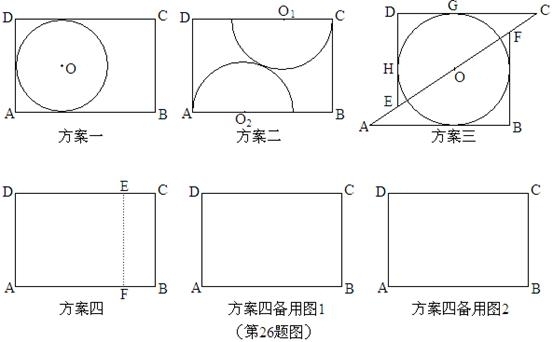
木匠黄师傅用长AB=3,宽BC=2的矩形木板做一个尽可能大的圆形桌面,他设计了四种方案:
方案一:直接锯一个半径最大的圆;
方案二:圆心O1,O2分别在CD,AB上,半径分别是O1C,O2A,锯两个外切的半![]() 圆拼成一个圆;
圆拼成一个圆;
方案三:沿对角线AC将矩形锯成两个三角形,适当平移三角形并锯一个最大的圆;
方案四:锯一块小矩形BCEF拼接到矩形AEFD下面,并利用拼成的木板锯一个尽可能大的圆。
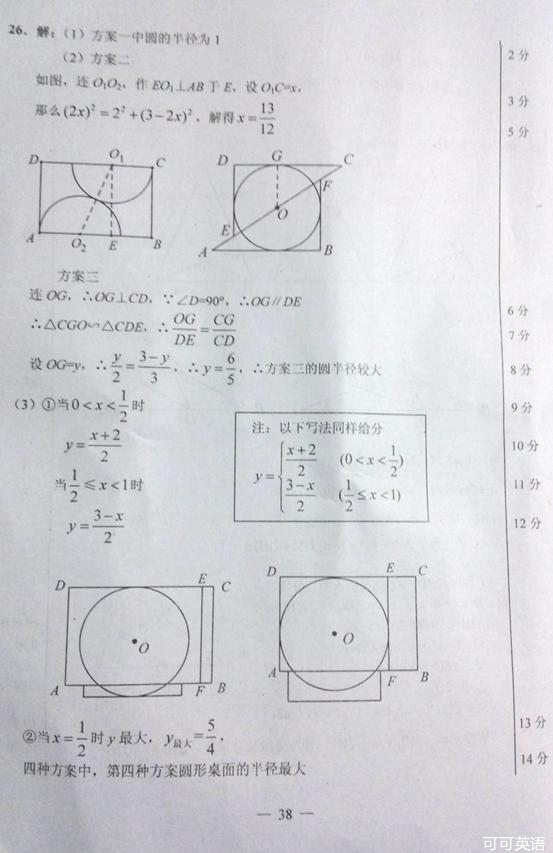
(1)写出方案一中的圆的半径;
(2)通过计算说明方案二和方案三中,哪个圆的半径较大?
(3)在方案四中,设CE= (
( ),圆的半径为
),圆的半径为 ,
,
①求 关于
关于 的函数解析式;
的函数解析式;
②当 取何值时圆的半径最大?最大半径是多少?并说明四种方案中,哪一个圆形桌面的半径最大?
取何值时圆的半径最大?最大半径是多少?并说明四种方案中,哪一个圆形桌面的半径最大?