(单词翻译:单击)
一、选择题(本大题共10小题,每小题3分,共30分)
1.﹣4的相反数【 】
A. 4 B. 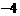 C.
C. 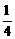 D.
D. 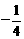

2.如图,∠1=40°,如果CD∥BE,那么∠B的度数为【 】
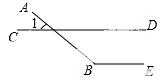
A. 160° B. 140° C. 60° D. 50°

考点:1.平角的定义;2.平行线的性质.
3.已知一个几何体的三视图如图所示,则该几何体是【 】

A. 圆柱 B. 圆锥 C. 球 D. 棱柱
【答案】A.
【解析】

4.若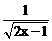 在实数范围内有意义,则x的取值范围是【 】
在实数范围内有意义,则x的取值范围是【 】
A.  B.
B. 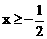 C.
C. 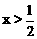 D.
D. 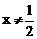

5.点P(2,﹣5)关于x轴对称的点的坐标为【 】
A. (﹣2,5) B. (2,5) C. (﹣2,﹣5) D. (2,﹣5)

6.化简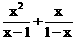 的结果是【 】
的结果是【 】
A. 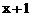 B.
B. 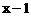 C.
C. 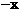 D.
D. 

考点:1.分式的加减法;2. 提公因式法因式分解.
7.已知一次函数y=kx﹣1,若y随x的增大而增大,则它的图象经过【 】
A. 第一、二、三象限 B. 第一、二、四象限 C. 第一、三、四象限 D. 第二、三、四象限

考点:一次函数图象与系数的关系.
8.若关于x的一元一次不等式组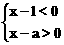 无解,则a的取值范围是【 】
无解,则a的取值范围是【 】
A. 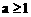 B.
B. 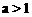 C.
C. 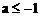 D.
D. 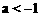

9.如图,△ABC中,AB=AC=18,BC=12,正方形DEFG的顶点E,F在△ABC内,顶点D,G分别在AB,AC上,AD=AG,DG=6,则点F到BC的距离为【 】
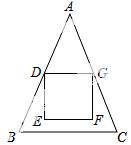
A. 1 B. 2 C. 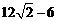 D.
D. 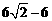

故选D.

考点:1.等腰三角形的性质;2.正方形的性质;3. 相似三角形的判定和性质;4.平行的判定和性质;5. 勾股定理;6.转换思想的应用.
10.如 图,一个半径为r的圆形纸片在边长为a(
图,一个半径为r的圆形纸片在边长为a(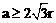 )的等边三角形内任意运动,则在该等边三角形
)的等边三角形内任意运动,则在该等边三角形 内,这个圆形纸片“不能接触到的部分”的面积是【 】
内,这个圆形纸片“不能接触到的部分”的面积是【 】
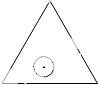
A. 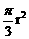 B.
B. 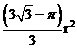 C.
C. 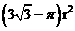 D.
D. 

故选C.
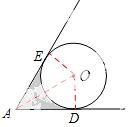
考点:1.面动问题;2. 等边三角形的性质;3. 切线的性质;4.扇形和三角形面积的计算;5.转换思想的应用.
二、填空题(本大题共8小题,每小 题3分,共24分)
题3分,共24分)
11.我国第一艘航母“辽宁舰”最大排水量为67500吨,这个数据用科学记数法可表示为________ 吨.
【答案】104.
【解析】
试题分析:根据科学记数法的定义,科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值. 在确定n的值时,看该数是大于或等于1还是小于1. 当该数大于或等于1时,n为它的整数位数减1;当该数小于1时,-n为它第 一个有效数字前0的个数(含小数点前的1个0).因此,
一个有效数字前0的个数(含小数点前的1个0).因此,
∵67500一共5位,∴67500=6.75×104.
考点:科学记数法.
12.因式分解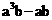 = _______.
= _______.

13.如果关于x的方程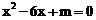 有两个相等的实数根,那么m= _______.
有两个相等的实数根,那么m= _______.

考点:1.抛物线与x轴的交点;2. 抛物线的轴对称性质.
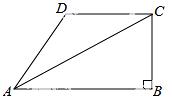
15.如图,四边形ABCD 中,AB∥DC,∠B=90°,连接AC,∠DAC=∠BAC.
中,AB∥DC,∠B=90°,连接AC,∠DAC=∠BAC. 若BC=4cm,AD=5cm,则AB=_______ cm.
若BC=4cm,AD=5cm,则AB=_______ cm.
【答案】8.
【解析】

考点:1.直角梯形的性质;2. 矩形的判定和性质;3.勾股定理;4. 平行的性质;5.等腰三角形的判定.
矩形的判定和性质;3.勾股定理;4. 平行的性质;5.等腰三角形的判定.
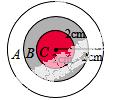
 16.在如图所示(A,B,C三个区域)的图形中随机地撒一把豆子,豆子落在 _______ 区域的可能性最大(填A或B或C).
16.在如图所示(A,B,C三个区域)的图形中随机地撒一把豆子,豆子落在 _______ 区域的可能性最大(填A或B或C).

17.如图,点A、B、C、D在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠OAD+∠OCD= _______ °.
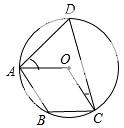

考点:1.圆内接四边形的性质;2.圆周角定理;3. 平行四边形的性质.
18.已知实数m,n满足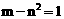 ,则代数式
,则代数式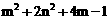 的最小值等于_______ .
的最小值等于_______ .

考点:1.配方法的应用;2. 偶次幂的非负数的性质;3.整体思想的应用.
三、解答题(本大题共10小题,共96分)
19.(10分)计算:
(1)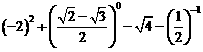 ;
;
(2)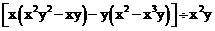 .
.
 【答案】(1)1;(2)
【答案】(1)1;(2)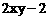 .
.
【解析】

考点:1. 有理数的乘方;2.零指数幂;3.二次根式化简;4.负整数指数幂;5. 整式的混合运算.
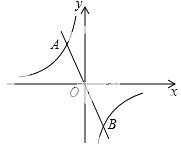
20.(8分)如图,正比例函数y=﹣2x与反比例函数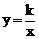 的图象相交于A(m,2
的图象相交于A(m,2 ),B两点.
),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)结合图象直接写出当﹣2x>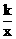 时,x的取值范围.
时,x的取值范围.
【答案】(1)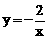 ,(1,﹣2);(2)x<﹣1或0<x<1.
,(1,﹣2);(2)x<﹣1或0<x<1.
【解析】

∵点A与点B关于原点对称,∴B点坐标为(1,﹣2).
(2)当x<﹣1或0< x<1时,﹣2x>
x<1时,﹣2x>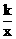 .
.
考点:1.反比例函数与一次函数的交点问题;2.曲线上点的坐标与方程的关系;3.数形结合思想的应用.
21.(8分)如图,海中有一灯塔P,它的周围8海里内有暗礁.海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?
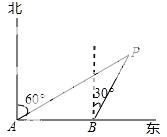
【答案】海轮不改变方向继续前进没有触礁的危险,理由见解析.
【解析】

考点:1.解直角三角形的应用(方向角问题);2. 锐角三角函数定义;3.特殊角的三角函数值;4.实数的大小比较.
22.(8分)九年级(1)班开展了为期一周的“敬老爱亲”社会活动,并根据学生做家务的时间来评价他们在活动中的表现,老师调查了全班50名学生在这次活动中做家务的时间,并将统计的时间(单位:小时)分成5组:
A.0.5≤x<1 B.1≤x<1.5 C.1.5≤x<2 D.2≤x<2.5 E.2.5≤x<3;并制成两幅不完整的统计图(如图):
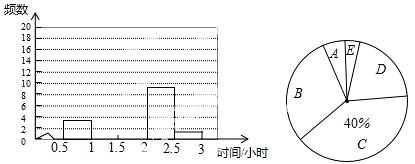
请根据图中提供的信息,解答下列问题:
(1)这次活动中学生做家务时间的中位数所在的组是 _______ ;
(2)补全频数分布直方图;
(3 )该班的小明同学这一周做家务2小时,他认为自己做家务的时间比班里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计知识说明理由.
)该班的小明同学这一周做家务2小时,他认为自己做家务的时间比班里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计知识说明理由.

(2)根据(1)得出的数据补图如下:
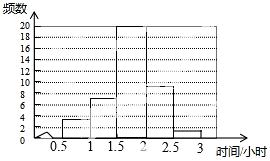
(3)符合实际.
设中位数为m,根据题意,m的取值范围是1.5≤m<2,
∵小明帮父母做家务的时间大于中位数,
∴他帮父母做家务的时间比班级中一半以上的同学多.
考点:1.频数分布直方图;3.扇形统计图;4.频数、频率和总量的关系;5.中位数.
23.(8 分)盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的概率是
分)盒中有x个黑球和y个白球,这些球除颜色外无其他差别.若从盒中随机取一个球,它是黑球的概率是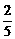 ;若往盒中再放
;若往盒中再放 进1个黑球,这时取得黑球的概率变为
进1个黑球,这时取得黑球的概率变为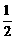 .
.
(1)填空:x= _______ ,y= _______ ;
(2)小王和小林利用x个黑球和y个白球进行摸球游戏.约定:从盒中随机摸取一个,接着从剩下的球中再随机摸取一个,若两球颜色相同则小王胜,若颜色不同则小林胜.求两个人获胜的概率各是多少?

(2)画树状图得:
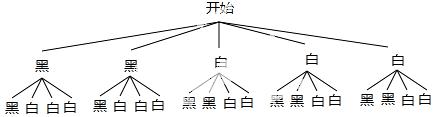
∵共有20种等可能的结果,两球颜色相同的有8种情况,颜色不同的有12种情况,
∴P(小王胜)=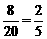 ,P(小林胜)=
,P(小林胜)=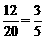 .
.
考点:1. 列表法或树状图法;2.概率公式;3.方程组的应用.
列表法或树状图法;2.概率公式;3.方程组的应用.
24.(8分)如图,AB是⊙O的直径,弦 CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
CD⊥AB于点E,点M在⊙O上,MD恰好经过圆心O,连接MB.
(1)若CD=16,BE=4,求⊙O的直径;
(2)若∠M=∠D,求∠D的度数.

【答案】(1)20;(2)30°.
【解析】

考点:1.垂径定理;2.勾股定理;3.圆周角定理;4.直角三角形两锐角的关系;5.方程思想的应用.
25.(9分)如图①,底面积为30cm2的空圆柱形容器内水平放置着由两个实心圆柱组成的“几何体”,现向容器内匀速注水,注满为止,在注水过程中,水面高度h(cm)与注水时间t(s)之间的关系如图②所 示.
示.
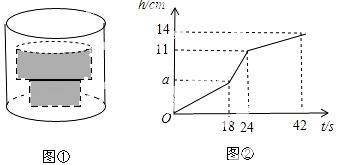
请根据图中提供的信息,解答下列问题:
(1)圆柱形容器的高为 _______ cm,匀速注水的水流速度为 _______ cm3/s;
 (2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
(2)若“几何体”的下方圆柱的底面积为15cm2,求“几何体”上方圆柱的高和底面积.
【答案】(1)14,5;(2)24cm2.
【解析】

答:“几何体”上方圆柱的底面积为24cm2.
考点:1.一次函数和一元一次方程的应用;2.直线上点的坐标与方程的关系.
26.(10分)如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EC,GD.
(1)求证:EB=GD;
(2)若∠DAB=60°,AB=2,AG=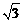 ,求GD的长.
,求GD的长.
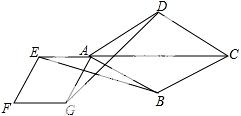

(2)如答图,连接BD交AC于点P,则BP⊥AC,
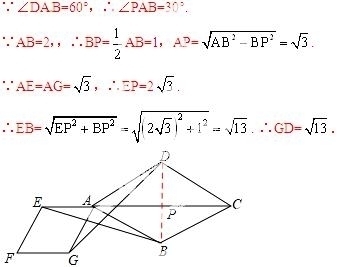
考点:1. 菱形的性质;2.相似多边形的性质;3.全等三角形的判定和性质;4.勾股定理;5.含30度角直角三角形的性质.
27.(13分)如图,矩形ABCD中,AB=3,AD=4,E为AB上一点,AE=1,M为射线AD上一动点,AM=a(a为大于0的常数),直线EM与直线CD交于点F,过点M作MG⊥EM,交直线BC于G.
(1)若M为边AD中点,求证:△EFG是等腰三角形;
(2)若点G与点C重合,求线 段MG的长;
段MG的长;
(3)请用含a的代数式表示△EFG的面积S,并指出S的最小整数值.
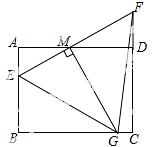
 长度,然后用含a的代数式表示△EFG的面积S,指出S的最小整数值.
长度,然后用含a的代数式表示△EFG的面积S,指出S的最小整数值.

又∵∠MCD+∠MFD=90°,∠AME+∠AEM=9 0°,∴∠AME=∠MCD.
0°,∴∠AME=∠MCD.
∵∠MAE=∠CDM=90°,∴△MAE∽△CDM. ∴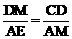 ,即
,即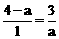 ,解得a=1或3.
,解得a=1或3.
代入CM=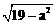 得CM=
得CM=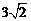 或
或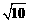 .
.
∵点G与点C重合,∴MG=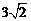 或
或 .
.
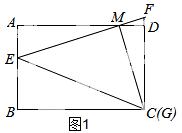
(3)①当点M在AD上时,如答图2,过点M作MN⊥BC交BC于点N,
∵AB=3,AD=4,AE=1,AM=a。∴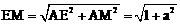 ,MD=AD-AM=4-a.
,MD=AD-AM=4-a.
∵∠A=∠MDF=90°,∠AME=∠DMF, ∴△MAE∽△MDF. ∴
∴△MAE∽△MDF. ∴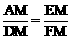 ,即
,即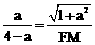 .
.
∴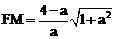 .∴
.∴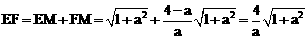 .
.
∵AD∥BC,∴∠MGN=∠DMG.
∵∠AME+∠AEM=90°,∠AME+∠DMG=90°,∴∠AME=∠DMG. ∴∠MGN=∠AME.

②当点M在AD的延长线上时,如图3,过点M作MN⊥BC,交BC延长线于点N,
∵AB=3,AD=4,AE=1,AM=a,∴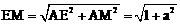 ,MD=a-4.
,MD=a-4.
∵DC∥AB,∴△MAE∽△MDF.∴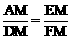 ,即
,即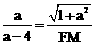 .∴
.∴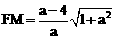 .
.
∴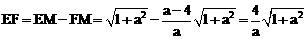 .
.
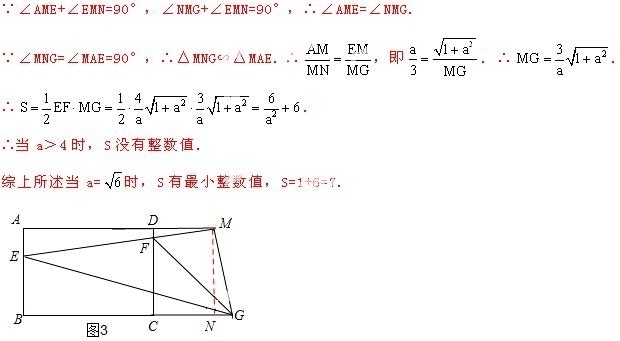
考点:1.单动点问题;2.矩形的性质;3.全等三角形的判定和性质;4. 等腰三角形的判定和;5.勾股定理;6.相似三角形的判定和性质;7.分类思想的应用.
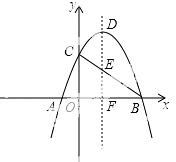
28.(14分)如图,抛物线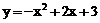 与x轴相交于A、B两点,与y轴交于C,顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F.
与x轴相交于A、B两点,与y轴交于C,顶点为D,抛物线的对称轴DF与BC相交于点E,与x轴相交于点F.
(1)求线段DE的长;
(2)设过E的直线与抛物线相交于M(x1,y1),N(x2,y2),试判断当|x1﹣x2|的值最小时,直线MN与x轴的位置关系,并说明理由;
(3)设P为x轴上的一点,∠DAO+∠DPO=∠α,当tan∠α=4时,求点P的坐标.
【答案】(1)2;(2)当|x1﹣x2|的值最小时,直线MN与x轴的位置关系是平行,理由见解析;(3)P1(19,0),P2(﹣17,0).
【解析】

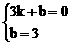 ,解得
,解得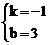 .
.

∴x1+x2=b1,x1x2=b1﹣3.
∵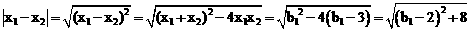 ,
,
∴当b1=2时,|x1﹣x2|最小值=2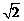 .
.
∵b1=2时,y=(2﹣b1)x+b1=2,∴直线MN∥x轴.
(3)如答图,∵D(1,4),∴tan∠DOF=4.
又∵tan∠α=4,∴∠DOF=∠α.
∵∠DOF=∠DAO+∠ADO=∠α, ∠DAO+∠DPO=∠α,∴∠DPO=∠ADO.
∠DAO+∠DPO=∠α,∴∠DPO=∠ADO.
∴△ADP∽△AOD. ∴AD2=AO•AP.
∵AF=2,DF=4,
∴AD2=AF2+DF2=20. ∴OP=19.
∴P1(19,0),P2( ﹣17,0).
﹣17,0).

考点:1.二次函数综合题;2.待定系数法的应用;3.曲线上点的坐标与方程的关系;4.一元二次方程根与系数的关系;5.配方法的应用;6.偶次幂的非负数性质;7.平行的判定;8.锐角三角函数定义;9.相似三角形的判定和性质.


