(单词翻译:单击)
一、选择题:本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项符合题目要求的。
1.若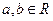 ,
,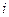 为虚数单位,且
为虚数单位,且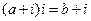 ,则( )
,则( )
A.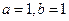 B.
B.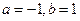 C.
C.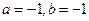 D.
D.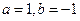
答案:D
2.设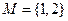 ,
,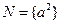 ,则“
,则“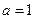 ”是“
”是“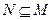 ”则( )
”则( )
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件
答案:A
3.设图一是某几何体的三视图,则该几何体的体积为( )
A. B.
B.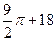
C.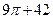 D.
D.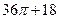
答案:B
4.通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由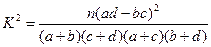 算得
算得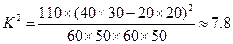
附表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是( )
A.在犯错误的概率不超过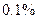 的前提下,认为“爱好该项运动与性别有关”
的前提下,认为“爱好该项运动与性别有关”
B.在犯错误的概率不超过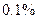 的前提下,认为“爱好该项运动与性别无关”
的前提下,认为“爱好该项运动与性别无关”
C.有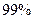 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”
D.有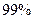 以上的把握认为“爱好该项运动与性别有关”
以上的把握认为“爱好该项运动与性别有关”
答案:C
5.设双曲线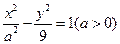 的渐近线方程为
的渐近线方程为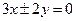 ,则
,则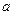 的值为( )
的值为( )
A.4 B.3 C.2 D.1
答案:C
6. 由直线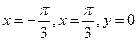 与曲线
与曲线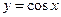 所围成的封闭图形的面积为( )
所围成的封闭图形的面积为( )
A.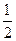 B.1 C.
B.1 C.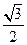 D.
D.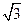
答案:D
7. 设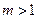 ,在约束条件
,在约束条件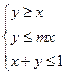 下,目标函数
下,目标函数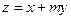 的最大值小于2,则
的最大值小于2,则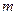 的取值范围为( )
的取值范围为( )
A.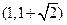 B.
B.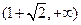 C.
C.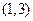 D.
D.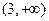
答案:A
8.设直线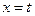 与函数
与函数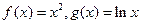 的图像分别交于点
的图像分别交于点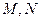 ,则当
,则当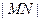 达到最小时
达到最小时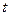 的值为( )
的值为( )
A.1 B.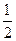 C.
C.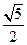 D.
D.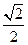
答案:D
二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分,把答案填在答题卡中对应题号的横线上。
一、选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题记分)
9.在直角坐标系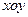 中,曲线C1的参数方程为
中,曲线C1的参数方程为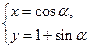 (
(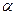 为参数)在极坐标系(与直角坐标系
为参数)在极坐标系(与直角坐标系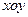 取相同的长度单位,且以原点O为极点,以
取相同的长度单位,且以原点O为极点,以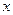 轴正半轴为极轴)中,曲线
轴正半轴为极轴)中,曲线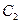 的方程为
的方程为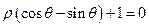 ,则
,则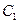 与
与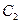 的交点个数为 。
的交点个数为 。
答案:2
10.设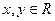 ,则
,则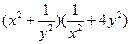 的最小值为 。
的最小值为 。
答案:9
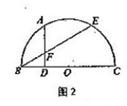
11.如图2,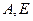 是半圆周上的两个三等分点,直径
是半圆周上的两个三等分点,直径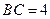 ,
,
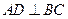 ,垂足为D,
,垂足为D, 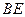 与
与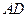 相交与点F,则
相交与点F,则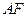 的长为 。
的长为 。
答案: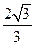
二、必做题(12~16题)
12、设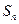 是等差数列
是等差数列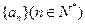 的前
的前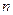 项和,且
项和,且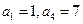 ,则
,则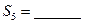
答案:25
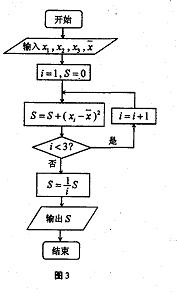
13、若执行如图3所示的框图,输入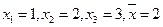 ,则输出的数等于 。
,则输出的数等于 。
答案: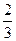
14、在边长为1的正三角形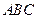 中,设
中,设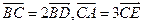 ,则
,则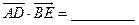 。
。
答案: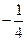
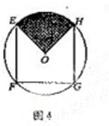
15、如图4, 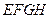 是以
是以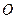 为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形
为圆心,半径为1的圆的内接正方形,将一颗豆子随机地扔到该圆内,用A表示事件“豆子落在正方形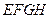 内”,B表示事件“豆子落在扇形
内”,B表示事件“豆子落在扇形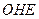 (阴影部分)内”,则
(阴影部分)内”,则
(1)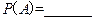 ;(2)
;(2)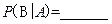
答案:(1)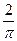 ;(2)
;(2)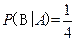
16、对于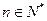 ,将
,将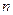 表示为
表示为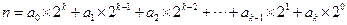 ,当
,当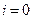 时,
时,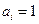 ,当
,当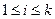 时,
时,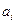 为0或1.记
为0或1.记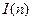 为上述表示中
为上述表示中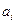 为0的个数,(例如
为0的个数,(例如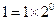 ,
,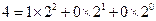 :故
:故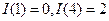 )则
)则
(1)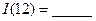 (2)
(2)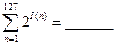
答案:(1)2;(2)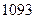
三.解答题:本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤。
17.(本小题满分12分)在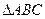 中,角
中,角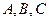 所对的边分别为
所对的边分别为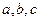 ,且满足
,且满足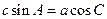 .
.
(I)求角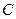 的大小;
的大小;
(II)求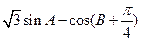 的最大值,并求取得最大值时角
的最大值,并求取得最大值时角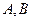 的大小.
的大小.
18. 某商店试销某种商品20天,获得如下数据:
日销售量(件) | 0 | 1 | 2 | 3 |
频数 | 1 | 5 | 9 | 5 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率。
(Ⅰ)求当天商品不进货的概率;
(Ⅱ)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。
19.(本题满分12分)如图5,在圆锥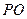 中,已知
中,已知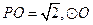 的直径
的直径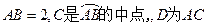 的中点.
的中点.
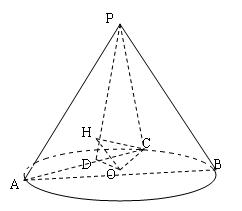
(I)证明: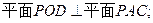
(II)求二面角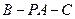 的余弦值.
的余弦值.
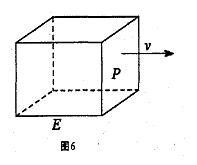
20. 如图6,长方形物体E在雨中沿面P(面积为S)的垂直方向作匀速移动,速度为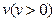 ,雨速沿E移动方向的分速度为
,雨速沿E移动方向的分速度为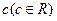 。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与
。E移动时单位时间内的淋雨量包括两部分:(1)P或P的平行面(只有一个面淋雨)的淋雨量,假设其值与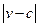 ×S成正比,比例系数为
×S成正比,比例系数为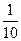 ;(2)其它面的淋雨量之和,其值为
;(2)其它面的淋雨量之和,其值为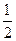 ,记
,记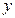 为E移动过程中的总淋雨量,当移动距离d=100,面积S=
为E移动过程中的总淋雨量,当移动距离d=100,面积S=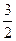 时。
时。
(Ⅰ)写出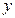 的表达式
的表达式
(Ⅱ)设0<v≤10,0<c≤5,试根据c的不同取值范围,确定移动速度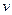 ,使总淋雨量
,使总淋雨量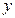 最少。
最少。
解析:(I)由题意知,E移动时单位时间内的淋雨量为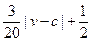 ,
,
故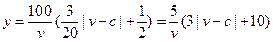 .
.
(II)由(I)知,当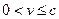 时,
时,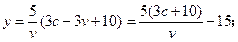
当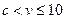 时,
时,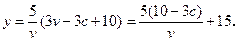
故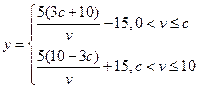 。
。
(1)当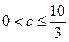 时,
时,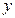 是关于
是关于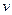 的减函数.故当
的减函数.故当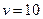 时,
时,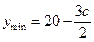 。
。
(2) 当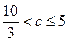 时,在
时,在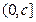 上,
上,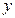 是关于
是关于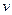 的减函数;在
的减函数;在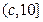 上,
上,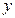 是关于
是关于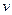 的增函数;故当
的增函数;故当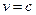 时,
时,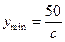 。
。
21.(本小题满分13分)
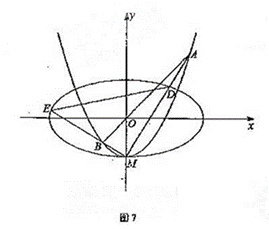
如图7,椭圆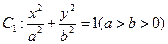 的离心率为
的离心率为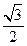 ,
,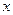 轴被曲线
轴被曲线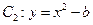 截得的线段长等于
截得的线段长等于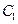 的长半轴长。
的长半轴长。
(Ⅰ)求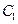 ,
,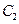 的方程;
的方程;
(Ⅱ)设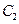 与
与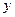 轴的交点为M,过坐标原点O的直线
轴的交点为M,过坐标原点O的直线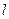 与
与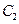 相交于点A,B,直线MA,MB分别与
相交于点A,B,直线MA,MB分别与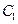 相交与D,E.
相交与D,E.
(i)证明: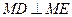 ;
;
(ii)记△MAB,△MDE的面积分别是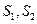 .问:是否存在直线
.问:是否存在直线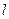 ,使得
,使得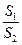 =
=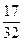 ?
?
请说明理由。
解析:(I)由题意知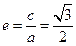 ,从而
,从而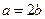 ,又
,又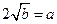 ,解得
,解得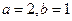 。
。
故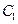 ,
,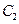 的方程分别为
的方程分别为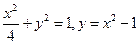 。
。
(II)(i)由题意知,直线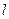 的斜率存在,设为
的斜率存在,设为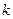 ,则直线
,则直线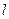 的方程为
的方程为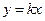 .
.
由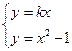 得
得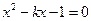 ,
,
设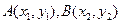 ,则
,则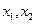 是上述方程的两个实根,于是
是上述方程的两个实根,于是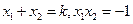 。
。
又点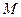 的坐标为
的坐标为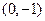 ,所以
,所以
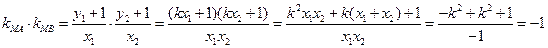
故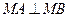 ,即
,即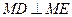 。
。
(ii)设直线的斜率为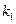 ,则直线的方程为
,则直线的方程为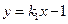 ,由
,由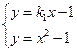 解得
解得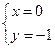 或
或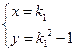 ,则点的坐标为
,则点的坐标为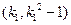
又直线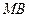 的斜率为
的斜率为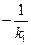 ,同理可得点B的坐标为
,同理可得点B的坐标为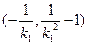 .
.
于是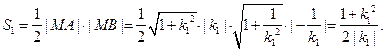
由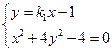 得
得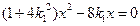 ,
,
解得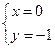 或
或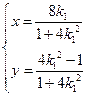 ,则点
,则点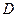 的坐标为
的坐标为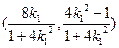 ;
;
又直线的斜率为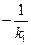 ,同理可得点
,同理可得点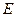 的坐标
的坐标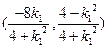
于是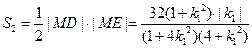
因此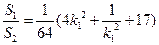
由题意知,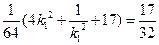 解得
解得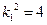 或
或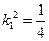 。
。
又由点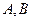 的坐标可知,
的坐标可知,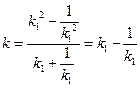 ,所以
,所以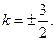
故满足条件的直线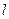 存在,且有两条,其方程分别为
存在,且有两条,其方程分别为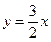 和
和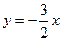 。
。
22.(本小题满分13分)
已知函数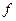 (
(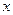 ) =
) =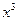 ,g (
,g (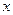 )=
)=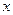 +
+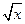 。
。
(Ⅰ)求函数h (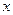 )=
)=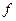 (
(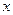 )-g (
)-g (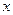 )的零点个数,并说明理由;
)的零点个数,并说明理由;
(Ⅱ)设数列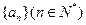 满足
满足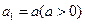 ,
,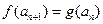 ,证明:存在常数M,使得对于任意的
,证明:存在常数M,使得对于任意的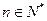 ,都有
,都有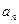 ≤
≤ 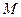 .
.
解析:(I)由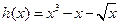 知,
知,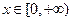 ,而
,而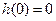 ,且
,且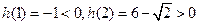 ,则
,则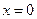 为
为 的一个零点,且
的一个零点,且 在
在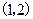 内有零点,因此
内有零点,因此 至少有两个零点
至少有两个零点
解法1: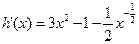 ,记
,记 ,则
,则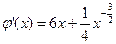 。
。
当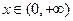 时,
时,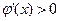 ,因此
,因此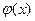 在
在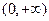 上单调递增,则
上单调递增,则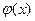 在
在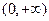 内至多只有一个零点。又因为
内至多只有一个零点。又因为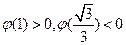 ,则
,则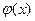 在
在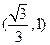 内有零点,所以
内有零点,所以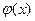 在
在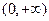 内有且只有一个零点。记此零点为
内有且只有一个零点。记此零点为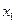 ,则当
,则当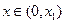 时,
时,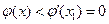 ;当
;当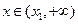 时,
时,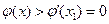 ;
;
所以,
当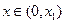 时,
时, 单调递减,而
单调递减,而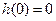 ,则
,则 在
在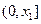 内无零点;
内无零点;
当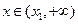 时,
时, 单调递增,则
单调递增,则 在
在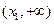 内至多只有一个零点;
内至多只有一个零点;
从而 在
在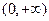 内至多只有一个零点。综上所述,
内至多只有一个零点。综上所述, 有且只有两个零点。
有且只有两个零点。
解法2: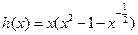 ,记
,记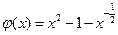 ,则
,则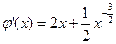 。
。
当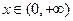 时,
时,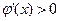 ,因此
,因此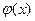 在
在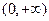 上单调递增,则
上单调递增,则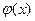 在
在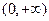 内至多只有一个零点。因此
内至多只有一个零点。因此 在
在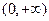 内也至多只有一个零点,
内也至多只有一个零点,
综上所述, 有且只有两个零点。
有且只有两个零点。
(II)记 的正零点为
的正零点为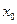 ,即
,即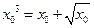 。
。
(1)当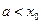 时,由
时,由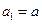 ,即
,即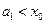 .而
.而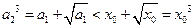 ,因此
,因此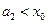 ,由此猜测:
,由此猜测: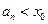 。下面用数学归纳法证明:
。下面用数学归纳法证明:
①当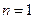 时,
时,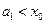 显然成立;
显然成立;
②假设当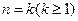 时,有
时,有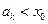 成立,则当
成立,则当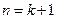 时,由
时,由
 知,
知,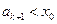 ,因此,当
,因此,当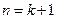 时,
时,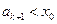 成立。
成立。
故对任意的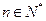 ,
,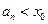 成立。
成立。
(2)当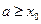 时,由(1)知,
时,由(1)知, 在
在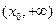 上单调递增。则
上单调递增。则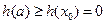 ,即
,即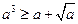 。从而
。从而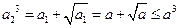 ,即
,即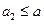 ,由此猜测:
,由此猜测: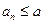 。下面用数学归纳法证明:
。下面用数学归纳法证明:
①当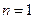 时,
时,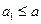 显然成立;
显然成立;
②假设当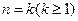 时,有
时,有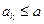 成立,则当
成立,则当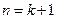 时,由
时,由
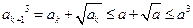 知,
知,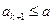 ,因此,当
,因此,当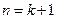 时,
时,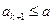 成立。
成立。
故对任意的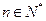 ,
,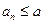 成立。
成立。
综上所述,存在常数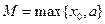 ,使得对于任意的
,使得对于任意的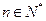 ,都有
,都有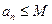 .
.