(单词翻译:单击)
2014年高考数学真题Word版(湖南卷+文科)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设命题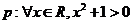 ,则
,则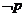 为( )
为( )
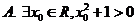
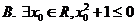
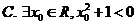
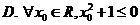
2.已知集合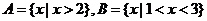 ,则
,则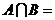 ( )
( )
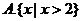
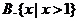
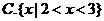
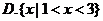
3.对一个容器为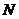 的总体抽取容量为
的总体抽取容量为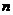 的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为
的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为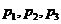 ,则( )
,则( )
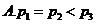
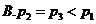
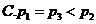
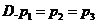
4.下列函数中,既是偶函数又在区间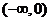 上单调递增的是( )
上单调递增的是( )
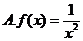
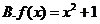
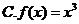
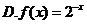
5.在区间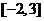 上随机选取一个数
上随机选取一个数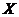 ,则
,则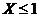 的概率为( )
的概率为( )
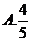
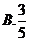
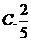
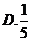
6.若圆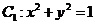 与圆
与圆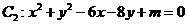 ,则
,则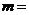 ( )
( )
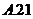
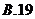
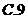
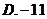
7.执行如图1所示的程序框图,如果输入的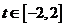 ,则输出的
,则输出的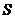 属于( ) A.
属于( ) A.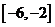 B.
B.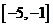 C.
C.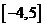 D.
D.
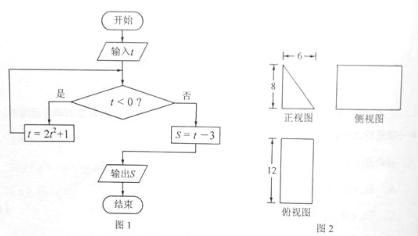
8.一块石材表示的几何体的三视图如图2所示,将石材切削、打磨、加工成球,则能得 到的最大球的半径等于( ) A.1 B.2 C.3 D.4 9.若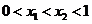 ,则( ) A.
,则( ) A. B.
B.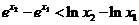 C.
C.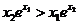 D.
D.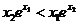
10.在平面直角坐标系中,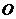 为原点,
为原点,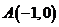 ,
,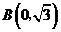 ,
,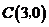 ,动点
,动点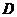 满足
满足 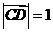 ,则
,则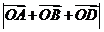 的取值范围是( ) A.
的取值范围是( ) A.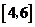 B.
B.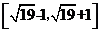 C.
C.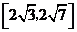 D.
D.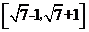
填空题:本大题共5小题,每小题5分,共25分.
复数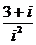 (
(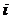 为虚数单位)的实部等于_________.
为虚数单位)的实部等于_________.
在平面直角坐标系中,曲线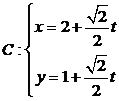 (
(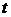 为参数)的普通方程为___________.
为参数)的普通方程为___________.
13.若变量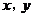 满足约束条件
满足约束条件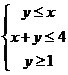 ,则
,则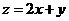 的最大值为_________.
的最大值为_________.
14.平面上以机器人在行进中始终保持与点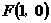 的距离和到直线
的距离和到直线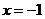 的距离相等.若
的距离相等.若
机器人接触不到过点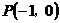 且斜率为
且斜率为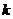 的直线,则
的直线,则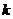 的取值范围是___________.
的取值范围是___________.
15.若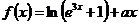 是偶函数,则
是偶函数,则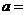 ____________.
____________.
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算过程.
16.(本小题满分12分)
已知数列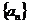 的前
的前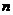 项和
项和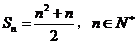 .
.
(I)求数列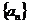 的通项公式;
的通项公式;
(II)设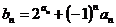 ,求数列
,求数列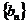 的前
的前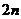 项和.
项和.
17.(本小题满分12分)
某企业有甲、乙两个研发小组,为了比较他们的研发水平,现随机抽取这两个小组往年
研发新产品的结果如下:
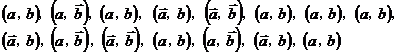
其中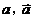 分别表示甲组研发成功和失败;
分别表示甲组研发成功和失败;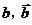 分别表示乙组研发成功和失败.
分别表示乙组研发成功和失败.
(I)若某组成功研发一种新产品,则给改组记1分,否记0分,试计算甲、乙两组研
发新产品的成绩的平均数和方差,并比较甲、乙两组的研发水平;
(II)若该企业安排甲、乙两组各自研发一种新产品,试估算恰有一组研发成功的概率.
(本小题满分12分)
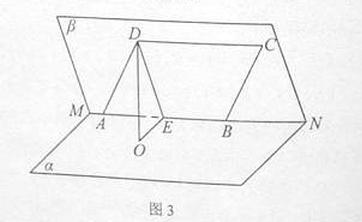
如图3,已知二面角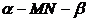 的大小为
的大小为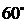 ,菱形
,菱形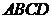 在面
在面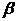 内,
内,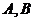 两点在棱
两点在棱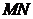 上,
上,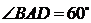 ,
,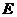 是
是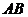 的中点,
的中点,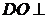 面
面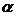 ,垂足为
,垂足为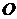 .
.
证明: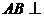 平面
平面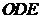 ;
;
(2)求异面直线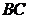 与
与 所成角的余弦值.
所成角的余弦值.
19.(本小题满分13分)
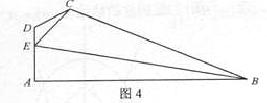
如图4,在平面四边形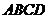 中,
中,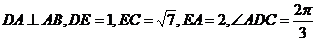 ,
,
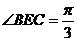
(1)求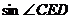 的值;
的值;
(2)求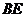 的长
的长
(本小题满分13分)
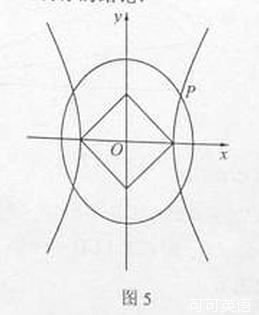
如图5, 为坐标原点,双曲线
为坐标原点,双曲线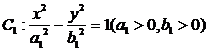 和椭圆
和椭圆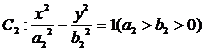 均过点
均过点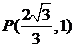 ,且以
,且以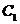 的两个顶点和
的两个顶点和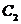 的两个焦点为顶点的四边形是面积为2的正方形.
的两个焦点为顶点的四边形是面积为2的正方形.
求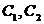 的方程;
的方程;
是否存在直线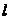 ,使得
,使得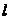 与
与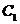 交于
交于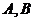 两点,与
两点,与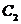 只有一个公共点,且
只有一个公共点,且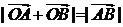 ?证明你的结论.
?证明你的结论.
21.(本小题满分13分)
已知函数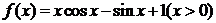 .
.
求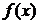 的单调区间;
的单调区间;
(2)记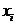 为
为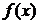 的从小到大的第
的从小到大的第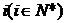 个零点,证明:对一切
个零点,证明:对一切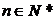 ,有
,有