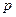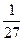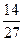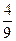(单词翻译:单击)
一、选择题:本题考查基础知识和基本运算.每小题5分,满分50分.

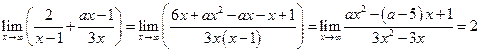 ,
,
故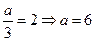
(4)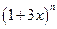 (其中
(其中 且
且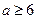 )的展开式中
)的展开式中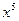 与
与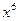 的系数相等,则
的系数相等,则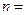
(A)6 (B)7
(C) 8 (D)9
解析:选B。 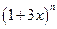 的通项为
的通项为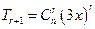 ,故
,故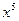 与
与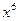 的系数分别为
的系数分别为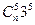 和
和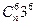 ,令他们相等,得:
,令他们相等,得: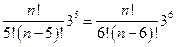 ,解得
,解得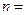 7
7

(7)已知a>0,b>0,a+b=2,则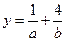 的最小值是
的最小值是
(A)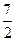 (B)4
(B)4
(C)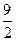 (D)5
(D)5

(C)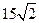 (D)
(D)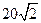
解析:选B ,由题意,AC为直径,设圆心为F,则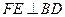 ,圆的标准方程为
,圆的标准方程为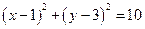 ,故
,故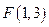 ,由此,易得:
,由此,易得: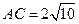 ,又
,又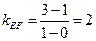 ,所以直线BD的方程为
,所以直线BD的方程为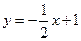 ,F到BD的距离为
,F到BD的距离为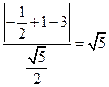 ,由此得,
,由此得,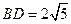 所以四边形ABCD的面积为
所以四边形ABCD的面积为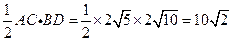

(A)-8 (B)8
(C)12 (D)13
解析:选D. 设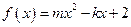 ,则方程
,则方程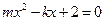 在
在 区间(0,1)内有两个不同的根等价于
区间(0,1)内有两个不同的根等价于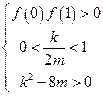 ,因为
,因为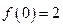 ,所以
,所以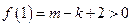 ,故抛物线开口向上,于是
,故抛物线开口向上,于是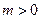 ,
,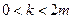 ,令
,令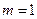 ,则由
,则由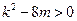 ,得
,得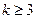 ,则
,则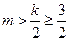 ,所以m至少为2,但
,所以m至少为2,但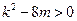 ,故k至少为5,又
,故k至少为5,又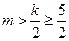 ,所以m至少为3,又由
,所以m至少为3,又由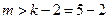 ,所以
,所以 m至少为4,……依次类推,发现当
m至少为4,……依次类推,发现当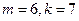 时,
时,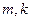 首次满足
首次满足
 所有条件,故
所有条件,故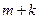 的最小值为13
的最小值为13
二、填空题:本大题共5小题,每小题5分,共25分,把答案写在答题卡相应位置上。

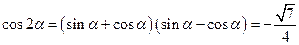 ,所以
,所以
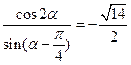
(15)设 圆
圆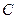 位于抛物线
位于抛物线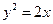 与直线
与直线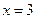 所组成的封闭区域(包含边界)内,则圆
所组成的封闭区域(包含边界)内,则圆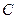 的半径能取到的最大值为
的半径能取到的最大值为
解析: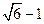 。 为使圆
。 为使圆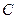 的半径取到最大值,显然圆心应该在x轴上且与直线
的半径取到最大值,显然圆心应该在x轴上且与直线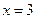 相切,设圆
相切,设圆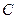 的半径为
的半径为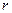 ,则圆
,则圆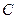 的方程为
的方程为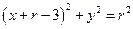 ,将其与
,将其与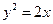 联立得:
联立得: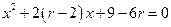 ,令
,令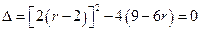 ,并由
,并由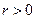 ,得:
,得: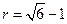
三、解答题:本大题共5小题,共75分,解答应写出文字说明,证明过程和清算步骤

又因为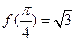 ,
,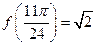
所以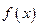 在
在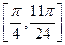 上的最小值为
上的最小值为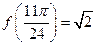
 (17)(本小题满分13分。(Ⅰ)小问5分(Ⅱ)小问8分.)
(17)(本小题满分13分。(Ⅰ)小问5分(Ⅱ)小问8分.)
某市公租房房屋位于A.B.C三个地区,设每位申请人只申请其中一个片区的房屋, 且申请其中任一个片区的房屋是等
且申请其中任一个片区的房屋是等 可能的,求该
可能的,求该 市的任4位申请人中:
市的任4位申请人中:
(Ⅰ)若有2人申请A片区房屋的概率;
(Ⅱ)申请的房屋在片区的个数的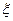 分布列与期望。
分布列与期望。
解析:(Ⅰ)所有可能的申请方式有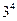 种,恰有2人申请A片区房源的申请方式有
种,恰有2人申请A片区房源的申请方式有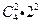 种,从而恰有2人申请A片区房源的概率为
种,从而恰有2人申请A片区房源的概率为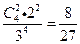
(Ⅱ)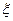 的所有可能值为1,2,3.又
的所有可能值为1,2,3.又
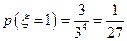 ,
,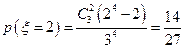 ,
,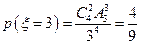
综上知,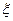 的分布列为:
的分布列为:
| 1 | 2 | 3 |
| | | |
从而有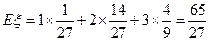
(18)(本小题满分13分。(Ⅰ)小题6分(Ⅱ)小题7分。)
设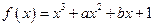 的导数
的导数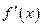 满足
满足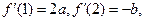 其中常数
其中常数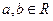 .
.
(Ⅰ)求曲线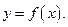 在点
在点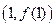 处的切线方程。
处的切线方程。
(Ⅱ)设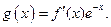 求函数
求函数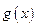 的极值。
的极值。
解析:(Ⅰ)因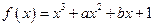 ,故
,故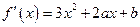 ,
,
令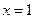 ,得
,得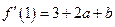 ,由已知
,由已知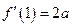 ,解得
,解得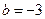
(19)本小题满分12分,(Ⅰ)小问5分,(Ⅱ)小问7分。
如图, 在四面体
在四面体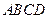 中,平面
中,平面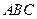 ⊥
⊥ 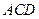 ,
, 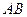 ⊥
⊥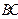 ,
,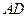 =
=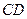 ,∠
,∠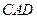 =
=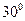
(Ⅰ)若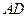 =2,
=2,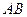 =2
=2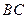 ,求四边形
,求四边形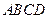 的体积。
的体积。
(Ⅱ)若二面角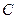 -
-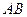 -
-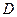 为
为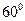 ,求异面直线
,求异面直线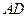 与
与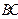 所成角的余弦值。
所成角的余弦值。
解析:(Ⅰ)如图所示,设F为AC的中点,由于AD=CD,所以DF⊥AC.
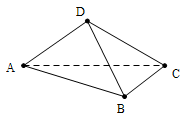
故由平面 ⊥
⊥  ,知DF⊥平面
,知DF⊥平面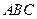 ,即
,即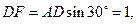 ,
,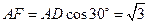 。在
。在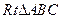 中,因
中,因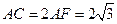 ,AB=2BC,有勾股定理易得
,AB=2BC,有勾股定理易得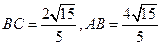 .
.
故四面体ABCD的体积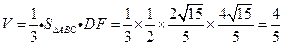
(Ⅱ)如图所示设G、H分别为变CD,BD的中点,则FG//AD,GH//BC,,从而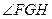 是异面直线
是异面直线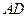 与
与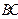 所成角或其补角。
所成角或其补角。

设E为边AB的中点,则EF//BC,由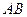 ⊥
⊥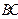 ,知
,知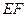 ⊥
⊥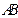 ,又由(Ⅰ)有DF⊥平面
,又由(Ⅰ)有DF⊥平面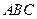 ,故由三垂线定理知
,故由三垂线定理知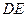 ⊥
⊥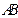 ,所以
,所以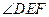 为二面角
为二面角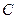 -
-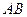 -
-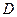 的平面角,由题设知
的平面角,由题设知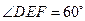 ,设AD=a,则DF=ADsinCAD=
,设AD=a,则DF=ADsinCAD=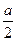
解析:(Ⅰ)由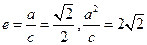 ,解得
,解得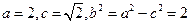 ,
,
故椭圆的标准方程为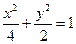
(Ⅱ)设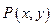 ,
,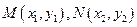 ,则由
,则由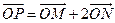 得
得
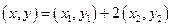 ,即
,即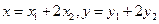 ,
,

(21)(本小题满 分12分。(Ⅰ)小问5分,(Ⅱ)小问7分)
分12分。(Ⅰ)小问5分,(Ⅱ)小问7分)
设实数数列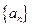 的前n项和
的前n项和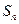 满足
满足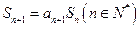
(Ⅰ)若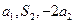 成等比数列,求
成等比数列,求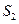 和
和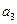
(Ⅱ)求证:对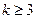 有
有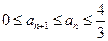 。
。
解析:(Ⅰ)由题意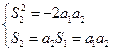 ,得
,得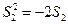 ,
,
由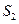 是等比中项知
是等比中项知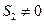 ,因此
,因此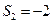 ,
,
由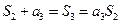 ,解得,
,解得,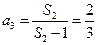
(Ⅱ)证明:有题设条件有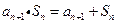 ,
,
故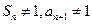 ,且
,且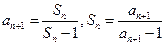
从而对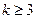 有
有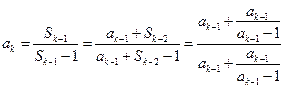 ①
①