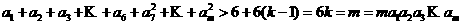(单词翻译:单击)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个备选项中,只有一项是符合题目要求的。
1.直线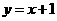 与圆
与圆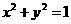 的位置关系为( )
的位置关系为( )
A.相切 B.相交但直线不过圆心 C.直线过圆心 D.相离
2.已知复数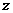 的实部为
的实部为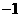 ,虚部为2,则
,虚部为2,则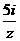 =( )
=( )
A.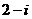 B.
B.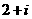 C.
C.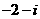 D.
D.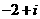
3.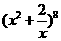 的展开式中
的展开式中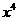 的系数是( )
的系数是( )
A.16 B.70 C.560 D.1120
4.已知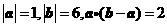 ,则向量
,则向量 与向量
与向量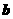 的夹角是( )
的夹角是( )
A.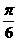 B.
B.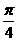 C.
C.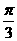 D.
D.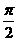

5.不等式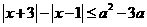 对任意实数
对任意实数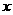 恒成立,则实数
恒成立,则实数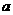 的取值范围为( )
的取值范围为( )
A. B.
B.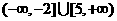 C.
C.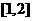 D.
D.
6.锅中煮有芝麻馅汤圆6个,花生馅汤圆5个,豆沙馅汤圆4个,这三种汤圆的外部特征完全相同。从中任意舀取4个汤圆,则每种汤圆都至少取到1个的概率为( )
A.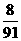 B.
B.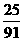 C.
C.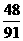 D.
D.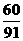
7.设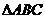 的三个内角
的三个内角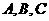 ,向量
,向量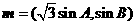 ,
,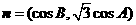 ,若
,若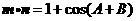 ,则
,则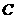 =( )
=( )
A.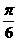 B.
B.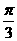 C.
C.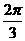 D.
D.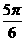
8.已知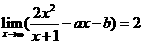 ,其中
,其中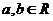 ,则
,则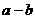 的值为( )
的值为( )
A.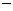 6 B.
6 B.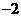 C.
C.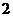 D.
D.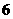
9.已知二面角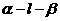 的大小为
的大小为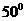 ,
,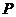 为空间中任意一点,则过点
为空间中任意一点,则过点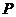 且与平面
且与平面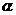 和平面
和平面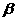 所成的角都是
所成的角都是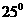 的直线的条数为( )
的直线的条数为( )
A.2 B.3 C.4 D.5
10.已知以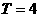 为周期的函数
为周期的函数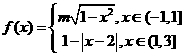 ,其中
,其中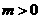 。若方程
。若方程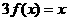 恰有5个实数解,则
恰有5个实数解,则 的取值范围为( )
的取值范围为( )
A.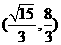 B.
B.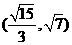 C.
C.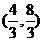 D.
D.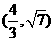
二、填空题:本大题共5小题,每小题5分,共25分.把答案写在答题卡相应位置上.
11.若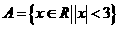 ,
,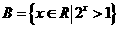 ,则
,则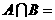 ___________.
___________.
12.若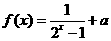 是奇函数,则
是奇函数,则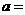 __________.
__________.
13.将4名大学生分配到3个乡镇去当村官,每个乡镇至少一名,则不同的分配方案有__________种(用数字作答).
14.设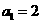 ,
,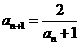 ,
,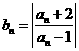 ,
,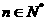 ,则数列
,则数列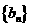 的通项公式
的通项公式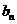 = __________.
= __________.
15.已知双曲线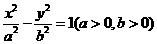 的左、右焦点分别为
的左、右焦点分别为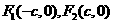 ,若双曲线上存在一点
,若双曲线上存在一点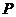 使
使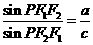 ,则该双曲线的离心率的取值范围是__________.
,则该双曲线的离心率的取值范围是__________.
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)
设函数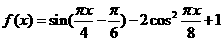 .
.
(Ⅰ)求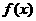 的最小正周期.
的最小正周期.
(Ⅱ)若函数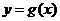 与
与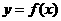 的图像关于直线
的图像关于直线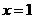 对称,求当
对称,求当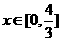 时
时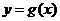 的最大值.
的最大值.
17.(本小题满分13分,(Ⅰ)问7分,(Ⅱ)问6分)
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为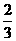 和
和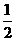 ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
(Ⅰ)两种大树各成活1株的概率;
(Ⅱ)成活的株数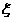 的分布列与期望.
的分布列与期望.
18.(本小题满分13分,(Ⅰ)问5分,(Ⅱ)问8分)
设函数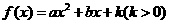 在
在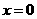 处取得极值,且曲线
处取得极值,且曲线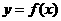 在点
在点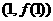 处的切线垂直于直线
处的切线垂直于直线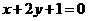 .
.
(Ⅰ)求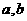 的值;
的值;
(Ⅱ)若函数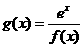 ,讨论
,讨论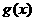 的单调性.
的单调性. 
19.(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
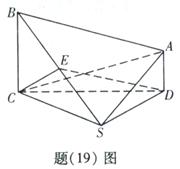
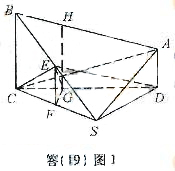
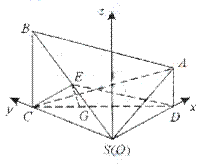
如题(19)图,在四棱锥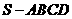 中,
中,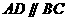 且
且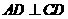 ;平面
;平面
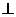 平面
平面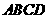 ,
,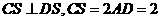 ;
;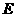 为
为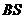 的中点,
的中点,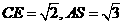 .求:
.求:
(Ⅰ)点 到平面
到平面 的距离;
的距离;
(Ⅱ)二面角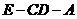 的大小.
的大小.
20.(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
已知以原点 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为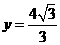 ,离心率
,离心率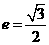 ,
, 是椭圆上的动点.
是椭圆上的动点.
(Ⅰ)若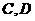 的坐标分别是
的坐标分别是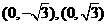 ,求
,求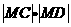 的最大值;
的最大值;
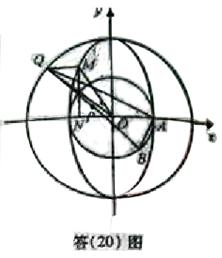
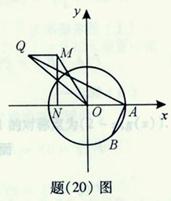
(Ⅱ)如题(20)图,点 的坐标为
的坐标为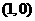 ,
,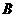 是圆
是圆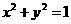 上的点,
上的点,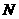 是点
是点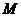 在
在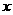 轴上的射影,点
轴上的射影,点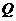 满足条件:
满足条件: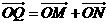 ,
,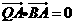 .求线段
.求线段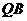 的中点
的中点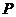 的轨迹方程;
的轨迹方程;
21.(本小题满分12分,(Ⅰ)问5分,(Ⅱ)问7分)
设 个不全相等的正数
个不全相等的正数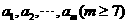 依次围成一个圆圈.
依次围成一个圆圈.
(Ⅰ)若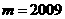 ,且
,且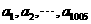 是公差为
是公差为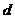 的等差数列,而
的等差数列,而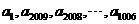 是公比为
是公比为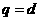 的等比数列;数列
的等比数列;数列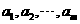 的前
的前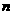 项和
项和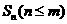 满足:
满足: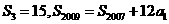 ,求通项
,求通项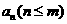 ;
;
(Ⅱ)若每个数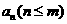 是其左右相邻两数平方的等比中项,求证:
是其左右相邻两数平方的等比中项,求证: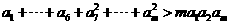 ;
;
2009年普通高等学校招生全国统一考试(重庆卷)
数学试题(理工农医类)答案
一、选择题:每小题5分,满分50分 .
(1) B (2) A (3) D (4) C (5) A (6) C
(7) C (8) D (9) B (10) B.
二.填空题:每小题5分,满分25分 .
(11) (0,3) (12) 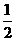 (13) 36 (14)
(13) 36 (14) 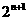 (15) (1,
(15) (1, 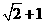 )
)
三.解答题:满分75分 .
(16)(本小题13分)
解:(Ⅰ)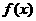 =
=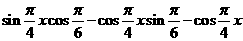
=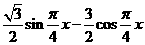
=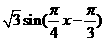
故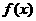 的最小正周期为T =
的最小正周期为T = 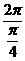 =8
=8
(Ⅱ)解法一:
在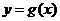 的图象上任取一点
的图象上任取一点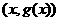 ,它关于
,它关于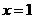 的对称点
的对称点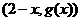 .
.
由题设条件,点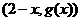 在
在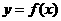 的图象上,从而
的图象上,从而
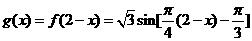 =
=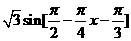 =
=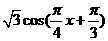
当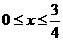 时,
时,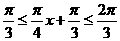 ,因此
,因此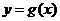 在区间
在区间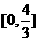 上的最大值为
上的最大值为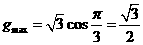
解法二:
因区间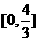 关于x = 1的对称区间为
关于x = 1的对称区间为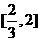 ,且
,且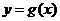 与
与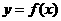 的图象关于x = 1对称,故
的图象关于x = 1对称,故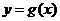 在
在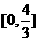 上的最大值为
上的最大值为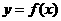 在
在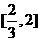 上的最大值
上的最大值
由(Ⅰ)知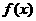 =
=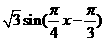
当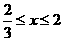 时,
时,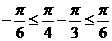
因此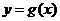 在
在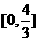 上的最大值为
上的最大值为
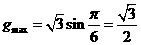 .
.
(17)(本小题13分)
解:设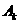 表示甲种大树成活k株,k=0,1,2
表示甲种大树成活k株,k=0,1,2
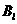 表示乙种大树成活l株,l=0,1,2
表示乙种大树成活l株,l=0,1,2
则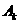 ,
,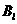 独立. 由独立重复试验中事件发生的概率公式有
独立. 由独立重复试验中事件发生的概率公式有
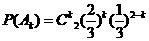 ,
, 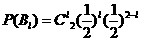 .
.
据此算得
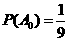 ,
, 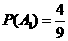 ,
, 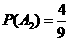 .
.
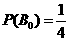 ,
, 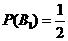 ,
, 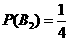 .
.
(Ⅰ) 所求概率为
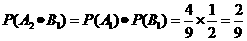 .
.
(Ⅱ) 解法一:
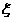 的所有可能值为0,1,2,3,4,且
的所有可能值为0,1,2,3,4,且
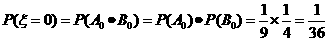 ,
,
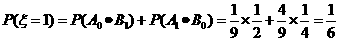 ,
,
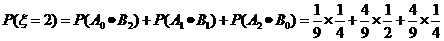
=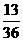 ,
,
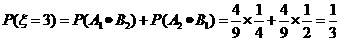 .
.
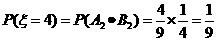 .
.
综上知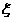 有分布列
有分布列
| 0 | 1 | 2 | 3 | 4 |
P | 1/36 | 1/6 | 13/36 | 1/3 | 1/9 |
从而,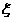 的期望为
的期望为
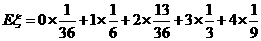
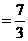 (株)
(株)
解法二:
分布列的求法同上
令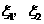 分别表示甲乙两种树成活的株数,则
分别表示甲乙两种树成活的株数,则

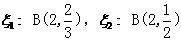
故有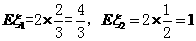
从而知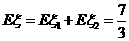
18、(本小题13分)
解(Ⅰ)因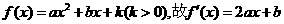
又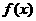 在x=0处取得极限值,故
在x=0处取得极限值,故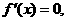 从而
从而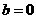
由曲线y=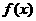 在(1,f(1))处的切线与直线
在(1,f(1))处的切线与直线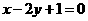 相互垂直可知
相互垂直可知
该切线斜率为2,即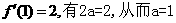
(Ⅱ)由(Ⅰ)知,
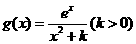
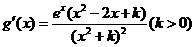
令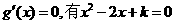
(1)当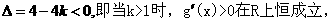
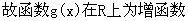
(2)当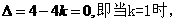
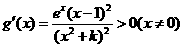
K=1时,g(x)在R上为增函数
(3)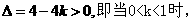 方程
方程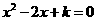 有两个不相等实根
有两个不相等实根
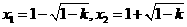
当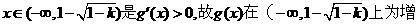 函数
函数
当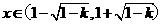 时,
时,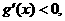 故
故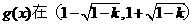 上为减函数
上为减函数
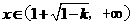 时,
时,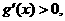 故
故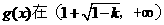 上为增函数
上为增函数
(19)(本小题12分)
解法一:
(Ⅰ)因为AD//BC,且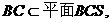 所以
所以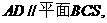 从而A点到平面
从而A点到平面 的距离等于D点到平面
的距离等于D点到平面 的距离。
的距离。
因为平面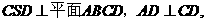 故
故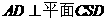 ,从而
,从而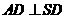 ,由AD//BC,得
,由AD//BC,得
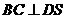 ,又由
,又由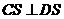 知
知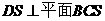 ,从而
,从而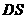 为点A到平面
为点A到平面 的距离,因此在
的距离,因此在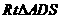 中
中
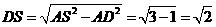
(Ⅱ)如答(19)图1,过E电作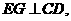 交
交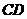 于点G,又过G点作
于点G,又过G点作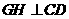 ,交AB于H,故
,交AB于H,故
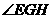 为二面角
为二面角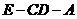 的平面角,记为
的平面角,记为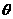 ,过E点作EF//BC,交
,过E点作EF//BC,交 于点F,连结GF,因平面
于点F,连结GF,因平面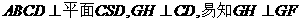 ,故
,故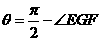 .
.
由于E为BS边中点,故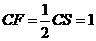 ,在
,在 中,
中,
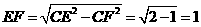 ,因
,因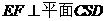 ,又
,又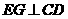
故由三垂线定理的逆定理得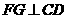 ,从而又可得
,从而又可得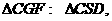
因此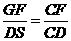 而在
而在 中,
中,
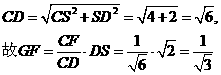
在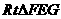 中,
中,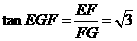 可得
可得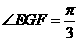 ,故所求二面角的大小为
,故所求二面角的大小为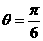
解法二:
(Ⅰ)如答(19)图2,以S(O)为坐标原点,射线OD,OC分别为x轴,y轴正向,建立空间坐标系,设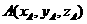 ,因平面
,因平面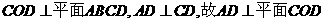
即点A在xoz平面上,因此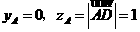
又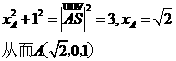
因AD//BC,故BC⊥平面CSD,即BCS与平面
yOx重合,从而点A到平面BCS的距离为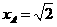 .
.
(Ⅱ)易知C(0,2,0),D(,0,0). 因E为BS的中点.
ΔBCS为直角三角形 ,
知 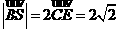
设B(0,2, 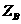 ),
),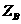 >0,则
>0,则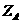 =2,故B(0,2,2),所以E(0,1,1) .
=2,故B(0,2,2),所以E(0,1,1) .
在CD上取点G,设G(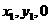 ),使GE⊥CD .
),使GE⊥CD .
由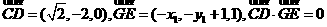 故
故
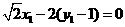 ①
①
又点G在直线CD上,即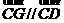 ,由
,由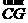 =(
=(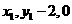 ),则有
),则有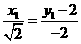 ②
②
联立①、②,解得G=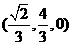 ,
,
故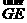 =
=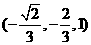 .又由AD⊥CD,所以二面角E-CD-A的平面角为向量
.又由AD⊥CD,所以二面角E-CD-A的平面角为向量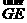 与向量
与向量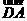 所成的角,记此角为
所成的角,记此角为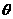 .
.
因为 =
=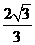 ,
,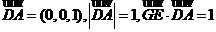 ,所以
,所以
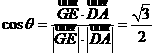
故所求的二面角的大小为 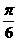 .
.
(20)(本小题12分)
解:(Ⅰ)由题设条件知焦点在y轴上,故设椭圆方程为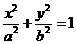 (a >b> 0 ).
(a >b> 0 ).
设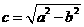 ,由准线方程
,由准线方程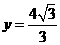 得.由
得.由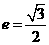 得
得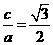 ,解得 a = 2 ,c =
,解得 a = 2 ,c = 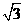 ,从而 b = 1,椭圆方程为
,从而 b = 1,椭圆方程为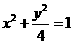 .
.
又易知C,D两点是椭圆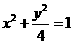 的焦点,所以,
的焦点,所以,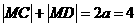
从而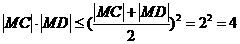 ,当且仅当
,当且仅当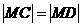 ,即点M的坐标为
,即点M的坐标为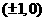 时上式取等号,
时上式取等号,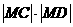 的最大值为4 .
的最大值为4 .
(II)如图(20)图,设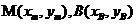
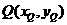 .因为
.因为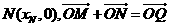 ,故
,故
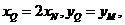
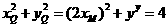 ①
①
因为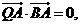
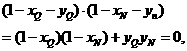
所以 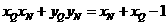 . ②
. ②
记P点的坐标为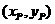 ,因为P是BQ的中点
,因为P是BQ的中点
所以 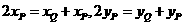
由因为 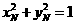 ,结合①,②得
,结合①,②得
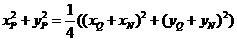
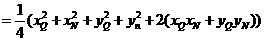
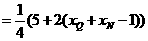
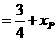
故动点P的估计方程为
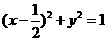
(21)(本小题12分)
解:(I)因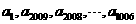 是公比为d的等比数列,从而
是公比为d的等比数列,从而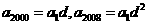 由
由 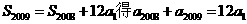 ,故
,故
解得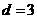 或
或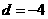 (舍去)。因此
(舍去)。因此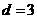
又 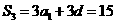 。解得
。解得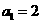
从而当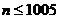 时,
时,
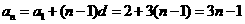
当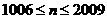 时,由
时,由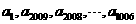 是公比为d的等比数列得
是公比为d的等比数列得
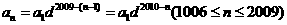
因此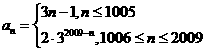
(II)由题意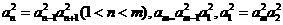 得
得
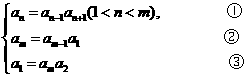
有①得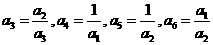 ④
④
由①,②,③得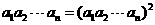 ,
,
故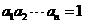 . ⑤
. ⑤
又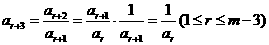 ,故有
,故有
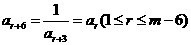 .⑥
.⑥
下面反证法证明: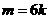
若不然,设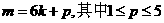
若取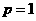 即
即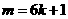 ,则由⑥得
,则由⑥得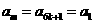 ,而由③得
,而由③得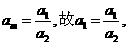
得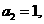 由②得
由②得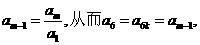 而
而
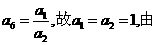 ④及⑥可推得
④及⑥可推得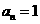 (
(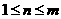 )与题设矛盾
)与题设矛盾
同理若P=2,3,4,5均可得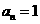 (
(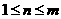 )与题设矛盾,因此
)与题设矛盾,因此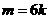 为6的倍数
为6的倍数
由均值不等式得
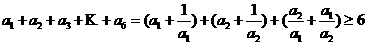
由上面三组数内必有一组不相等(否则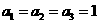 ,从而
,从而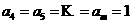 与题设矛盾),故等号不成立,从而
与题设矛盾),故等号不成立,从而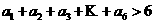
 又
又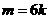 ,由④和⑥得
,由④和⑥得
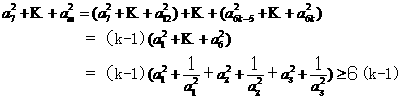
因此由⑤得