(单词翻译:单击)
一、选择题:本大题共10小题,每小题5分,共50分。在每小题给出的四个备选项中,只有一项是符合题目要求的。

3.曲线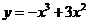 在点(1,2)处的切线方程为
在点(1,2)处的切线方程为
(A) 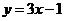 (B)
(B) 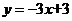 (C)
(C)
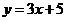 (D)
(D)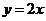
【命题意图】本题考查利用导数求函数的切线,是容易题.
【解析】∵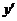 =
=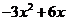 ,∴切线斜率为3,则过(1,2)的切线方程为
,∴切线斜率为3,则过(1,2)的切线方程为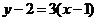 ,即
,即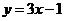 ,故选A.
,故选A.
【答案】A
4.从一堆苹果中任取10只称得它的质量如下(单位:克)
125 120 122 105 130 114 116 95 120 134
则样本数据落在[114.5,124.5) 内的频率为
内的频率为
(A)0.2 (B)0.3 (C)0.4 (D)0.5

6.设 =
=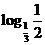 ,
,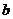 =
=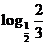 ,
, =
=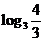 ,则
,则 ,
,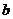 ,
, 的大小关系是
的大小关系是
(A)  <
<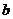 <
< (B)
(B) 
 <
<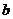 <
< (C)
(C) 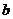 <
< <
< (D)
(D) 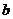 <
< <
<
【命题意图】本题考查对数函数的图像与性质,是简单题.
【解析】∵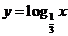 与
与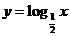 在(0,+∞)都是减函数,且0<
在(0,+∞)都是减函数,且0<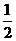 <1,0<
<1,0<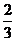 <1,
<1,
∴ =
=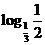 >0,
>0,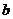 =
=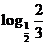 >0,
>0,
又∵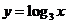 在(0,+∞)上是增函数,且0<
在(0,+∞)上是增函数,且0<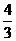 <1,∴
<1,∴ =
=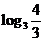 <0,即
<0,即 最小,只有B符合,故选B.
最小,只有B符合,故选B.
【答案】B
7.若函数 =
=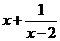 (
( >2)在
>2)在 =
= 处有最小值,则
处有最小值,则 =
=
(A)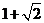 (B)
(B)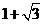
 (C)3 (D)4
(C)3 (D)4

9.设双曲线的左准线与两条渐近线交于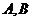 两点,左焦点为在以
两点,左焦点为在以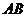 才为之直径的圆内,则该双曲线的离心率的取值范围为
才为之直径的圆内,则该双曲线的离心率的取值范围为
(A)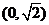 (B)
(B)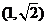 (C)
(C) 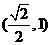 (D)
(D)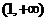
【命题意图】本题考查双曲线的性质、点与圆的位置关系,考查学生转化与化归能力、解不等式能力,难度较大.
【解析】双曲线的左准线为 =
=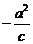 ,渐近线方程为
,渐近线方程为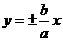 ,联立解得(
,联立解得(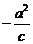 ,
,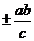 ),
),
∴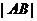 =
=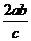 ,根据题意得,
,根据题意得,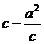 <
<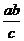 ,即
,即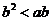 ,即
,即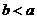 ,即
,即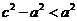 ,即
,即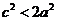 ,即
,即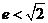 ,又
,又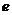 >1,,1<
>1,,1<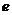 <
<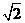 ,故选B.
,故选B.
【答案】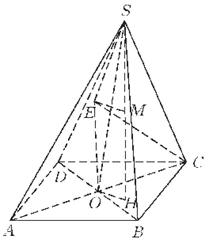 B
B
10.高为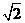 的四棱锥
的四棱锥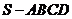 的底面是边长为
的底面是边长为 1的正方形,点
1的正方形,点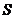 、
、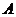 、
、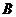 、
、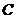 、
、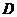 均在半径为1的同一球面上,则底面
均在半径为1的同一球面上,则底面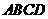 的中心与顶点
的中心与顶点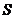 之间的距离为
之间的距离为
(A)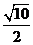 (B)
(B)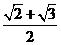 (C)
(C)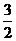 (D)
(D)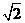
【命题意图】本题考查四棱锥与其外接球的相关知识,考查空间想象能力、转化化归能力以及运算求解能力,是难题.
【解析】如图,设四棱锥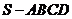 的外接球球心为
的外接球球心为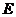 ,则
,则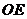 ⊥面
⊥面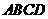 ,在
,在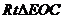 中,
中,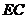 =1,
=1,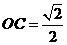 ,∴
,∴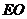 =
=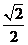 ,
,
∵设四棱锥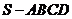 的高
的高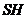 =
=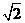 ,∴
,∴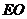 ∥
∥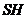 且
且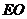 =
=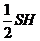 ,
,
取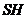 的中点
的中点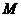 ,连结
,连结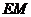 ,则四边形
,则四边形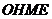 为矩形,∴
为矩形,∴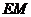 ⊥
⊥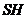 ,
,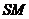 =
=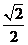 ,在
,在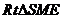 中,
中,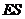 =1,则
=1,则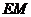 =
=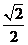 ,∴
,∴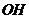 =
=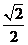 ,
,
 在
在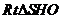 中,
中, =
=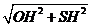 =
=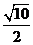 ,故选A.
,故选A.
【答案】A
二.填空题,本大题共5小题,每小题5分,共25分,把答案填写在答题卡相应位置上
11. 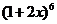 的展开式中
的展开式中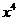 的系数是___________.
的系数是___________.

14.从甲、乙等10位同学中任选3位去参加某项活动,则所选3位中有甲但没有乙的概率为_________
【命题意图】本题考查组合计算和等可能事件的概率计算,是中档题.
【解析】10位同学任选3人共有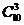 种选法,其中含甲不含乙共有
种选法,其中含甲不含乙共有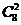 种选法,故所选3位中有甲但没有乙的概率为
种选法,故所选3位中有甲但没有乙的概率为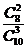 =
=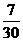 .
.
【答案】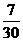
15.若实数 ,
,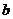 ,
, 满足
满足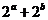 =
=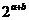 ,
,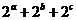 =
=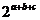 ,则
,则 的最大值是 .
的最大值是 .
【命题意图】本题考查基本不等式的应用,指数、对数等相关知识,考查了转化与化归思想,是难题.
【解析】∵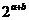 =
=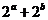 ≥
≥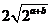 ,∴
,∴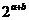 ≥4,
≥4,
又∵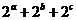 =
=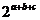 ,∴
,∴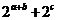 =
=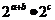 ,∴
,∴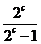 =
=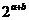 ≥4,即
≥4,即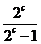 ≥4,即
≥4,即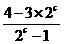 ≥0,∴
≥0,∴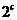 ≤
≤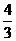 ,∴
,∴ ≤
≤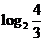 =
=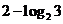 ,∴
,∴ 的最大值为
的最大值为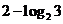 .
.
【答案】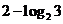

三、解答是:本大题共6小题,共75分 .解
.解 答应写出文字说明、证明过程或演算步骤.
答应写出文字说明、证明过程或演算步骤.
16.(本小题满分 13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)设{
13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)设{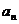 }是公比为正数的等比数列,
}是公比为正数的等比数列,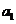 =2,
=2,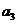 =
=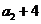 .
.
(Ⅰ)求{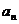 }的通项公式;
}的通项公式;
(Ⅱ)设{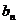 }是首项为1,公差为2的等差数列,求数列{
}是首项为1,公差为2的等差数列,求数列{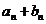 }的前
}的前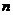 项和
项和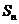 .
.
【命题意图】本题考查等比数列的通项公式和等比数列、等差数列的前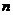 项和公式,考查函数与方程思想和运算求解能力,是简单题.
项和公式,考查函数与方程思想和运算求解能力,是简单题.
【解析】(Ⅰ)设等比数列{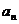 }的公比为
}的公比为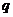 ,由
,由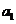 =2,
=2,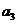 =
=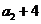 知,
知,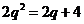 ,
,
即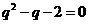 ,解得
,解得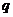 =2或
=2或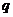 =-1(舍去),∴
=-1(舍去),∴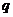 =2,
=2,
∴{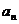 }的通项公式
}的通项公式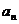 =
=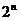 (
(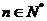 );
);
(Ⅱ) 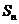 =
=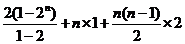 =
=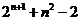 .
.
17.(本小题满分13分,(Ⅰ)小问6分,(Ⅱ)小问7分.)某市公租房的房源位于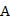 、
、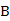 、
、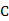 三个片区.设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的.求该市的4位申请人中:
三个片区.设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的.求该市的4位申请人中:
(Ⅰ)没有人申请A片区房源的概率;
(Ⅱ)每个片区的房源都有人申 请的概
请的概 率.
率.
【命题意图】本题考查应用排列组合知识和两个计数原理求等可能事件的概率、独立重复试验,考查运用概率知识分析解决问题能力,是中档题.
【解析】(Ⅰ) (法1)设事件A表示 “没有人申请A片区房源”所有可能的申请方式有
“没有人申请A片区房源”所有可能的申请方式有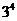 种,其中没有人申请A片区房源方式有
种,其中没有人申请A片区房源方式有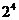 种,则没有人申请A片区房源的概率为
种,则没有人申请A片区房源的概率为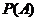 =
=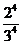 =
=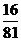 .
.
(法2)设“申请A片区房源”为事件A,
∵每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,
∴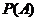 =
=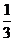 ,
,
对每位申请房源作为一次试验,应为每人申请房源相 互独立,4人申请房源可以看成4次独立重复试验,故没人申请A片房源的概率为
互独立,4人申请房源可以看成4次独立重复试验,故没人申请A片房源的概率为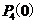 =
=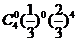 =
=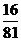 ;
;
(Ⅱ)记“每个片区的房源都有人申请”为事件B,所有可能的申请方式有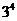 种,其中每个片区的房源都有人申请的方式有
种,其中每个片区的房源都有人申请的方式有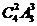 种,
种,
∴每个片区的房源都有人申请的概率为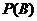 =
=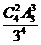 =
=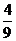 .
.
18. (本小题满分13分,(Ⅰ)小问7分,(Ⅱ)小问6分.)设函数 =
=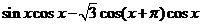 (
(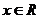 ).
).
(Ⅰ)求 的最小正周期;
的最小正周期;
(Ⅱ)若函数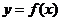 的图象按
的图象按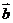 =(
=(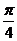 ,
,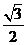 )平移后得到函数
)平移后得到函数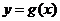 的图象,求
的图象,求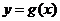 在[0,
在[0,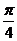 ]上的
]上的 最大值.
最大值.
【命题意图】本题考查诱导公式、两 角和与差的正余弦公式、周期公式、向量平移、三角函数在某个区间上的最值求法和运算求解能力,是中档题.
角和与差的正余弦公式、周期公式、向量平移、三角函数在某个区间上的最值求法和运算求解能力,是中档题.
【解析】(Ⅰ)  =
=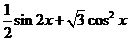 =
=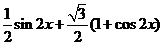
=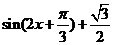 ,
,
∴ 的最小正周期为
的最小正周期为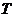 =
=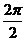 =
=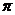 .
.
(Ⅱ)依题意得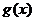 =
=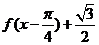 =
=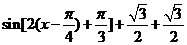
=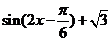
当 ∈[0,
∈[0,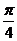 ]时,
]时,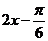 ∈
∈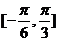 ,∴
,∴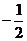 ≤
≤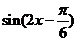 ≤
≤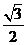 ,
,
∴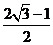 ≤
≤ ≤
≤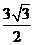 , ∴
, ∴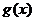 在[0,
在[0,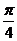 ]的最大值为
]的最大值为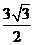 .
.
19. (本小题满分12分,(Ⅰ)小问5分,(Ⅱ )小问7分.)
)小问7分.)
设 =
=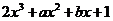 的导数为
的导数为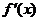 ,若函数
,若函数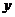 =
=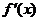 的图象关于直线
的图象关于直线 =
=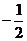 对称,且
对称,且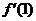 =0.
=0.
(Ⅰ)求实数 ,
,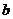 的值;
的值;
(Ⅱ)求函数 的极值.
的极值.
【命题意图】本题考查考查利用导数求函数的极值、二次函数的图像与性质,考查方程与不等式思想、转化和化归思想,属容易题.
【解析】(Ⅰ)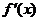 =
=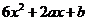 ,
,
∵若函数
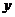 =
=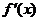 的图象关于直线
的图象关于直线 =
=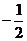 对称,且
对称,且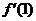 =0,
=0,
∴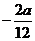 =
=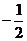 且
且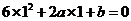 ,解得
,解得 =3,
=3,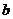 =-12.
=-12.
(Ⅱ)由(Ⅰ)知 =
=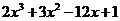 ,
,
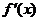 =
=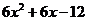 =
=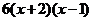 ,
,
 的变化如下:
的变化如下:
| (-∞,-2) | -2 | (-2,1) | 1 | (1,+∞) |
| + | 0 | - | 0 | + |
|
| 极大值21 |
| 极小值-6 |
|
∴当 =-2时,
=-2时, 取极大值,极大值为21,当
取极大值,极大值为21,当 =1时,
=1时, 取极小值,极小值为-6.
取极小值,极小值为-6.
20.(本小题满分12分,(Ⅰ)小问6分,(Ⅱ )小问6分.如图,在四面体
)小问6分.如图,在四面体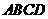 中,平面
中,平面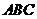 ⊥平面
⊥平面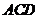 ,
,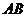 ⊥
⊥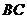 ,
,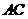 =
=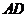 =2,
=2,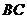 =
=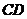 =1.
=1.

(Ⅰ)求四面体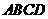 的体积;
的体积;
(Ⅱ)求二面角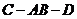 的平面角的正切值.
的平面角的正切值.
【命题意图】本题考查简单几何体的体积计算、二面角的求法,考查空间想象能力、推理论证能力、运算求解能力及转化与化归思想,是中档题.
【解析】(Ⅰ) 如图,过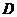 作
作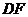 ⊥
⊥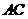 于
于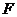 ,∵平面
,∵平面 ⊥平面
⊥平面 ,
,
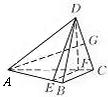
∴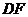 ⊥平面
⊥平面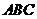 ,则
,则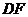 是四面体
是四面体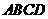 的面
的面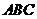 上的高,
上的高,
设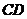 中点为
中点为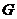 ,∵
,∵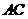 =
=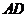 =2,∴
=2,∴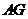 ⊥
⊥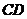 ,
,
∴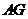 =
=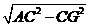 =
=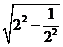 =
=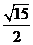 ,
,
∵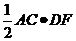 =
=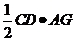 , ∴
, ∴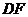 =
=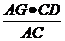 =
=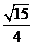 ,
,
在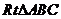 中,
中,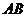 =
=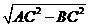 =
=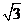 ,∴
,∴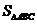 =
=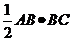 =
=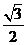 ,
,
∴四棱锥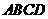 的体积
的体积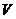 =
=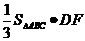 =
=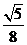 .
.
(Ⅱ)(几何法)过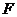 作
作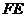 ⊥
⊥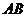 与
与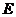 ,连结
,连结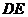 ,由(Ⅰ)知
,由(Ⅰ)知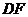 ⊥面
⊥面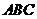 ,
,
由三垂线定理知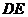 ⊥
⊥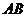 ,∴
,∴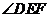 为二面角
为二面角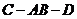 的平面角,
的平面角,
在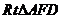 中,
中,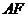 =
=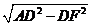 =
=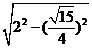 =
=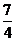 ,
,
在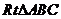 中,
中,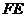 ∥
∥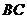 , ∴
, ∴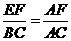 , ∴
, ∴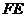 =
=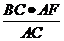 =
=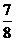 ,
,
在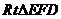 中,
中,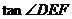 =
=
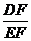 =
=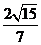 .
.

21. ( 本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分.)如图,椭圆的中心为原点
本小题满分12分,(Ⅰ)小问4分,(Ⅱ)小问8分.)如图,椭圆的中心为原点 ,离心率
,离心率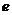 =
=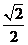 ,一条准线的方程是
,一条准线的方程是 =
=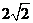 .
.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设动点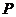 满足:
满足: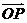 =
=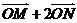 ,其中
,其中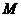 ,
,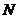 是椭圆上的点,直线
是椭圆上的点,直线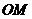 与
与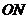 的斜率之积为
的斜率之积为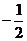 .问:是否存在定点
.问:是否存在定点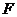 ,使得
,使得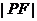 与点
与点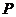 到直线
到直线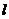 :
: =
=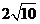 的距离之比为定值?若存在,求
的距离之比为定值?若存在,求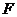 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
【命题意图】本题考查了椭圆标准方程的求解与椭圆的定植问题,考查学生综合运用知识解决问题能力、运算求解能力和探究问题能力,难度较大.
【解析】(Ⅰ) ∵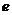 =
=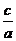 =
=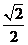 ,
,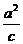 =
=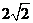 ,解得
,解得 =2,
=2,
 =
=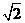 ,∴
,∴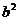 =
=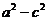 =2,
=2,
∴椭圆的标准方程为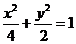 ;
;
(Ⅱ)设P( ,
,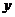 ),
),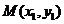 ,
,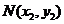 ,
, 则由
则由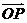 =
=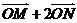 ,得
,得
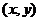 =
=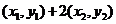 =
=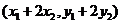 ,
,
∴ =
=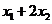 ,
,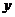 =
=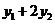 ,
,
∵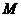 ,
,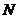 在椭圆
在椭圆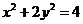 上,∴
上,∴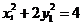 ,
,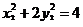 ,
,
∴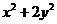 =
=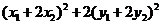 =
=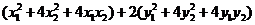
=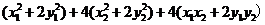 =
=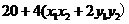 .
.
设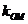 ,
,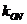 分别表示直线
分别表示直线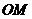 ,
,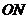 的斜率,由题设条件知,
的斜率,由题设条件知,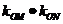 =
=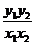 =
=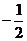 ,
,
∴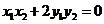 , ∴
, ∴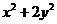 =20,
=20,
∴点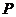 在椭圆
在椭圆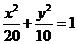 上,该椭圆的右焦点为
上,该椭圆的右焦点为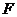 (
(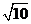 ,0),离心率
,0),离心率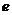 =
=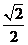 ,右准线为
,右准线为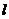 :
: =
=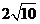 ,
,
∴根据椭圆的第二定义,存在定点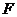 (
(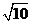 ,0),使得
,0),使得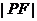 与点
与点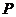 到直线
到直线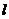 的距离之比为定值.
的距离之比为定值.