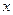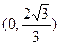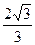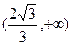(单词翻译:单击)
第I卷
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.若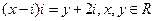 ,则复数
,则复数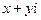 =( )
=( )
A.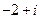 B.
B.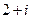 C.
C.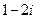 D.
D.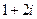
答案:B
解析: 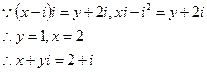
2.若全集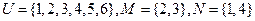 ,则集合
,则集合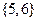 等于( )
等于( )
A.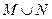 B.
B.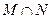 C.
C.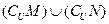 D.
D.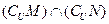
答案:D
解析: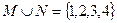 ,
,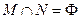 ,
,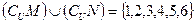 ,
,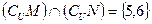
3.若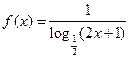 ,则
,则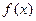 的定义域为( )
的定义域为( )
A. B.
B.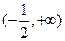 C.
C.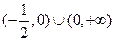 D.
D.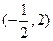
答案:C 解析: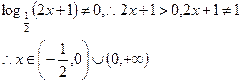
4.曲线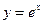 在点A(0,1)处的切线斜率为( )
在点A(0,1)处的切线斜率为( )
A.1B.2C.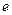 D.
D.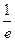
答案:A解析: 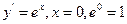
5.设{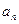 }为等差数列,公差d = -2,
}为等差数列,公差d = -2,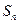 为其前n项和.若
为其前n项和.若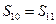 ,则
,则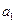 =( )
=( )
A.18B.20C.22D.24
答案:B解析: 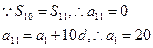
6.观察下列各式:则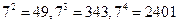 ,…,则
,…,则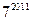 的末两位数字为( )
的末两位数字为( )
A.01B.43C.07D.49
答案:B 解析: 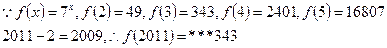
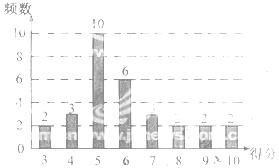
7.为了普及环保知识,增强环保意识,某大学随即抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为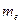 ,众数为
,众数为 ,平均值为
,平均值为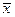 ,则( )
,则( )
A.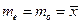 B.
B.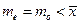 C.
C.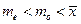 D.
D.
答案:D计算可以得知,中位数为5.5,众数为5所以选D
8.为了解儿子身高与其父亲身高的关系,随机抽取5对父子的身高数据如下:
父亲身高x(cm) | 174 | 176 | 176 | 176 | 178 |
儿子身高y(cm) | 175 | 175 | 176 | 177 | 177 |
则y对x的线性回归方程为
A.y = x-1B.y = x+1C.y = 88+ 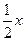 D.y = 176
D.y = 176
 C线性回归方程
C线性回归方程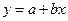 ,
,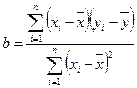 ,
,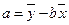
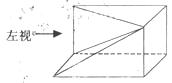
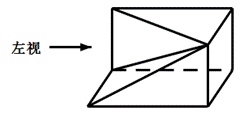
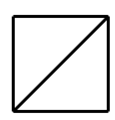
9.将长方体截去一个四棱锥,得到的几何体如右图所示,则该几何体的左视图为( )

答案:D左视图即是从正左方看,找特殊位置的可视点,连起来就可以得到答案。
10.如图,一个“凸轮”放置于直角坐标系X轴上方,其“底端”落在原点O处,一顶点及
中心M在Y轴正半轴上,它的外围由以正三角形的顶点为圆心,以正三角形的边长为半径的三段等弧组成.

今使“凸轮”沿X轴正向滚动前进,在滚动过程中“凸轮”每时每刻都有一个“最高点”,其中心也在不断移动位置,则在“凸轮”滚动一周的过程中,将其“最高点”和“中心点”所形成的图形按上、下放置,应大致为( )
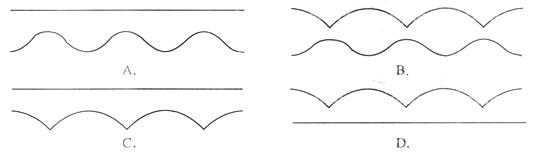
答案:A根据中心M的位置,可以知道中心并非是出于最低与最高中间的位置,而是稍微偏上,随着转动,M的位置会先变高,当C到底时,M最高,排除CD选项,而对于最高点,当M最高时,最高点的高度应该与旋转开始前相同,因此排除B ,选A。
第II卷
二.填空题:本大题共5小题,每小题5分,共25分.
11、11.已知两个单位向量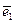 ,
,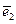 的夹角为
的夹角为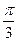 ,若向量
,若向量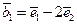 ,
,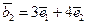 ,则
,则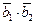 =___.
=___.
答案:-6. 解析:要求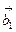 *
*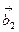 ,只需将题目已知条件带入,得:
,只需将题目已知条件带入,得:
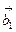 *
*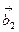 =(
=(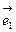 -2
-2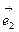 )*(3
)*(3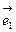 +4
+4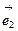 )=
)=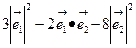
其中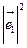 =1,
=1,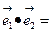 =
=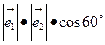 =1*1*
=1*1*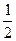 =
=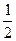 ,
,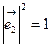 ,
,
带入,原式=3*1—2*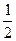 —8*1=—6
—8*1=—6
(PS: 这道题是道基础题,在我们做过的高考题中2007年广东文科的第四题,以及寒假题海班文科讲义73页的第十题,几乎是原题。考查的就是向量的基本运算。送分题(*^__^*) )
12.若双曲线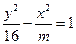 的离心率e=2,则m=____.
的离心率e=2,则m=____.
答案:48.解析:根据双曲线方程: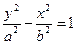 知,
知, 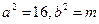 ,并在双曲线中有:
,并在双曲线中有: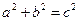 ,
,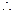 离心率e=
离心率e=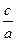 =2
=2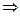
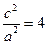 =
=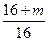 ,
,
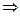 m=48
m=48
(PS: 这道题虽然考的是解析几何,大家印象中的解几题感觉都很难,但此题是个灰常轻松得分题(~ o ~)~zZ。你只需知道解几的一些基本定义,并且计算也不复杂。在2008年安徽文科的第14题以及2009福建文科的第4题,同时在我们寒假题海班讲义文科教材第145页的第3题,寒假理科教材第149页第30题都反复训练过。O(∩_∩)O。。所谓认真听课,勤做笔记,有的就是这个效果!!)
13.下图是某算法的程序框图,则程序运行后输出的结果是____.

答案:27. 解析:由框图的顺序,s=0,n=1,s=(s+n)n=(0+1)*1=1,n=n+1=2,依次循环
S=(1+2)*2=6,n=3,注意此刻3>3仍然是否,所以还要循环一次
s=(6+3)*3=27,n=4,此刻输出,s=27.
(PS: 程序框图的题一直是大家的青睐,就是一个循环计算的过程。2010天津文科卷的第3题,考题与此类似。在我们寒假文科讲义117页的第2题做过与此非常类似的,无非更改些数字。基础是关键!)
14.已知角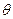 的顶点为坐标原点,始边为x轴的正半轴,若
的顶点为坐标原点,始边为x轴的正半轴,若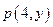 是角
是角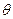 终边上一点,且
终边上一点,且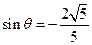 ,则y=_______.
,则y=_______.
答案:—8. 解析:根据正弦值为负数,判断角在第三、四象限,再加上横坐标为正,断定该角为第四象限角。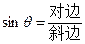 =
=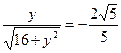
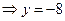
(PS:大家可以看到,步骤越来越少,不就意味着题也越来越简单吗?并且此题在我们春季班教材3第10页的第5题,出现了一模一样。怎么能说高考题是难题偏题。)
15.对于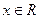 ,不等式
,不等式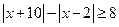 的解集为_______
的解集为_______
答案: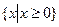 解析:两种方法,方法一:分三段,
解析:两种方法,方法一:分三段,
当x<-10时,-x-10+x-2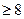 ,
, 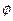
当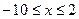 时,x+10-x+2
时,x+10-x+2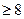 ,
,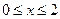
当x>2时, x+10-x+2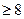 , x>2
, x>2
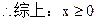
方法二:用绝对值的几何意义,可以看成到两点-10和2的距离差大于等于8的所有点的集合,画出数轴线,找到0到-10的距离为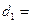 10,到2的距离为
10,到2的距离为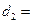 2,
2,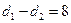 ,并当x往右移动,距离差会大于8,所以满足条件的x的范围是
,并当x往右移动,距离差会大于8,所以满足条件的x的范围是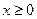 .
.
(PS: 此题竟出现在填空的最后一道压轴题,不知道神马情况。。。。。更加肯定考试考的都是基础,并且!!在我们除夕班的时候讲过一道一摸一样,只是换了数字而已的题型,在除夕教材第10页的15题。。太强悍啦!!几乎每道都是咱上课讲过的题目~~所以,亲爱的童鞋们,现在的你上课还在聊Q, 睡觉流口水吗??)
三.解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
某饮料公司对一名员工进行测试以便确定其考评级别.公司准备了两种不同的饮料共5杯,其颜色完全相同,并且其中3杯为A饮料,另外2杯为B饮料,公司要求此员工一一品尝后,从5杯饮料中选出3杯A饮料.若该员工3杯都选对,则评为优秀;若3杯选对2杯,则评为良好;否则评为及格.假设此人对A和B两种饮料没有鉴别能力.
(1)求此人被评为优秀的概率;
(2)求此人被评为良好及以上的概率.
解:(1)员工选择的所有种类为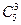 ,而3杯均选中共有
,而3杯均选中共有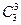 种,故概率为
种,故概率为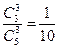 .
.
(2)员工选择的所有种类为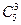 ,良好以上有两种可能:3杯均选中共有
,良好以上有两种可能:3杯均选中共有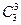 种;
种;
‚:3杯选中2杯共有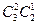 种。故概率为
种。故概率为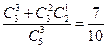 .
.
解析:本题考查的主要知识是排列组合与概率知识的结合,简单题。
17.(本小题满分12分)
在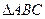 中,
中,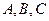 的对边分别是
的对边分别是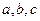 ,已知
,已知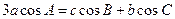 .
.
(1)求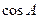 的值;
的值;
(2)若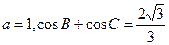 ,求边
,求边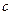 的值.
的值.
解:(1)由 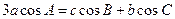 正弦定理得:
正弦定理得:
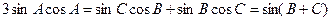
及: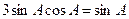 所以
所以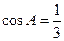 。
。
(2)由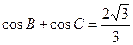
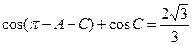 展开易得:
展开易得:
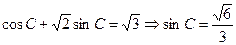
正弦定理: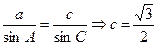
【解析】本题考查的主要知识三角函数及解三角形问题,题目偏难。第一问主要涉及到正弦定理、诱导公式及三角形内角和为180°这两个知识点的考查属于一般难度;第二问同样是对正弦定理和诱导公式的考查但形势更为复杂。
18.(本小题满分12分)
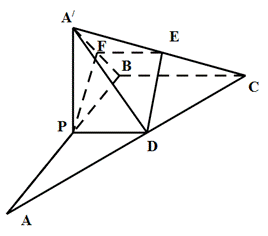
如图,在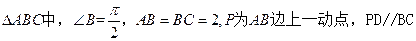 交AC于 点D,现将
交AC于 点D,现将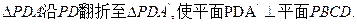
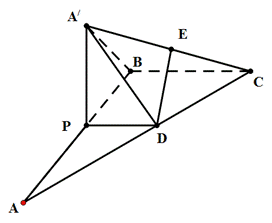
(1)当棱锥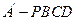 的体积最大时,求PA的长;
的体积最大时,求PA的长;
(2)若点P为AB的中点,E为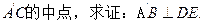
解(1)设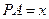 ,则
,则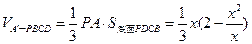
令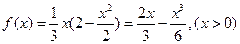
则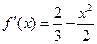
|
|
|
|
|
|
|
|
| 单调递增 | 极大值 | 单调递减 |
由上表易知:当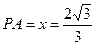 时,有
时,有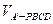 取最大值。
取最大值。
证明:
(2)作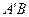 得中点F,连接EF、FP由已知得:
得中点F,连接EF、FP由已知得: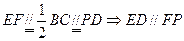
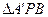 为等腰直角三角形,
为等腰直角三角形,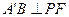 所以
所以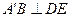 .
.
19.(本小题满分12分)
已知过抛物线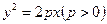 的焦点,斜率为
的焦点,斜率为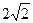 的直线交抛物线于
的直线交抛物线于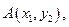
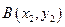 (
(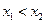 )两点,且
)两点,且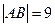 .
.
(1)求该抛物线的方程;
(2)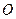 为坐标原点,
为坐标原点,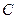 为抛物线上一点,若
为抛物线上一点,若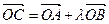 ,求
,求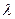 的值.
的值.
解析:(1)直线AB的方程是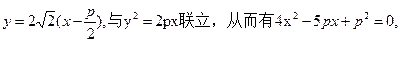
所以: ,由抛物线定义得:
,由抛物线定义得: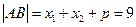 ,所以p=4,
,所以p=4,
抛物线方程为: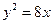
(2)、由p=4,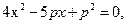 化简得
化简得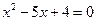 ,从而
,从而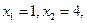
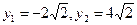 ,从而A:(1,
,从而A:(1,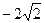 ),B(4,
),B(4,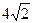 )
)
设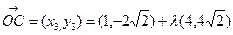 =
=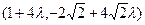 ,又
,又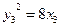 ,即
,即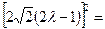 8(4
8(4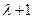 ),即
),即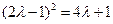 ,解得
,解得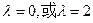
20.(本小题满分13分)
设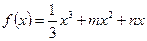 .
.
(1)如果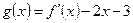 在
在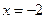 处取得最小值
处取得最小值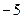 ,求
,求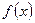 的解析式;
的解析式;
(2)如果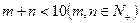 ,
,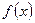 的单调递减区间的长度是正整数,试求
的单调递减区间的长度是正整数,试求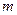 和
和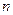
的值.(注:区间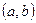 的长度为
的长度为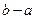 )
)
.解:(1)已知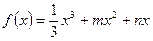 ,
,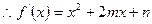
又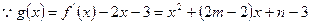 在
在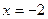 处取极值,
处取极值,
则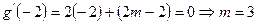 ,又在
,又在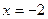 处取最小值-5.
处取最小值-5.
则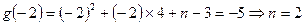
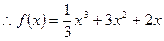
(2)要使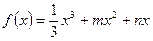 单调递减,则
单调递减,则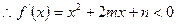
又递减区间长度是正整数,所以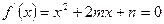 两根设做a,b。即有:
两根设做a,b。即有:
b-a为区间长度。又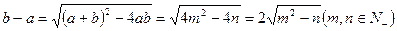
又b-a为正整数,且m+n<10,所以m=2,n=3或,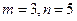 符合。
符合。
21.(本小题满分14分)
(1)已知两个等比数列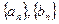 ,满足
,满足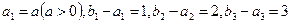 ,若数列
,若数列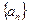 唯一,求
唯一,求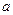 的值;
的值;
(2)是否存在两个等比数列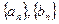 ,使得
,使得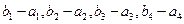 成公差
成公差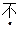 为
为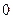 的等差数列?若存在,求
的等差数列?若存在,求 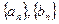 的通项公式;若
的通项公式;若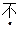 存在,说明理由.
存在,说明理由.
解:(1)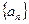 要唯一,
要唯一,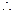 当公比
当公比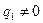 时,由
时,由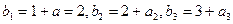 且
且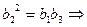
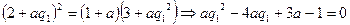 ,
,
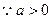 ,
,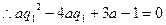 最少有一个根(有两个根时,保证仅有一个正根)
最少有一个根(有两个根时,保证仅有一个正根)
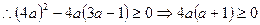 ,此时满足条件的a有无数多个,不符合。
,此时满足条件的a有无数多个,不符合。
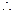 当公比
当公比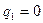 时,等比数列
时,等比数列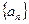 首项为a,其余各项均为常数0,唯一,此时由
首项为a,其余各项均为常数0,唯一,此时由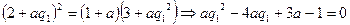 ,可推得
,可推得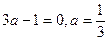 符合
符合
综上: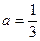 。
。
(2)假设存在这样的等比数列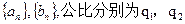 ,则由等差数列的性质可得:
,则由等差数列的性质可得: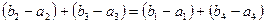 ,整理得:
,整理得: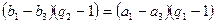
要使该式成立,则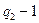 =
=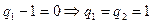 或
或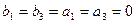 此时数列
此时数列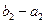 ,
,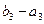 公差为0与题意不符,所以不存在这样的等比数列
公差为0与题意不符,所以不存在这样的等比数列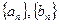 。
。