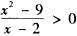(单词翻译:单击)
一、 选择题:本大题共10小题,每小题5分,共50分, 在每小题给出的四个选项中,只有一项是符合题目要求的
1. 若复数z=1+i (i为虚数单位) 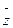 是z的共轭复数 , 则
是z的共轭复数 , 则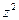 +
+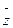 ²的虚部为
²的虚部为
A 0 B -1 C 1 D -2
【答案】A
【解析】考查复数的基本运算
2  若全集U={x∈R|x2≤4} A={x∈R||x+1|≤1}的补集CuA为
若全集U={x∈R|x2≤4} A={x∈R||x+1|≤1}的补集CuA为
A |x∈R |0<x<2| B |x∈R |0≤x<2|
C |x∈R |0<x≤2| D |x∈R |0≤x≤2|
【答案】C
【解析】考查集合的基本运算
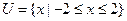 ,
,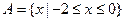 ,则
,则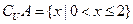 .
.
3.设函数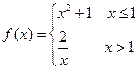 ,则f(f(3))=
,则f(f(3))=
【答案】D
4.若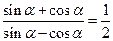 ,则tan2α=
,则tan2α=
【答案】B
【解析】主要考查三角函数的运算,分子分母同 时除以
时除以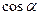 可得
可得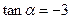 ,带入所求式可得结果.
,带入所求式可得结果.
5. 观察下列事实|x|+|y|=1的不同整数解(x,y)的个数为4 , |x|+|y|=2的不同整数解(x,y)的个数为8, |x|+|y|=3的不同整数解(x,y)的个数为12 ….则|x|+|y|=20的不同整数解(x,y)的个数为
A.76 B.80 C.86 D.92
【答案】B
【解析】本题主要为数列的应用题,观察可得不同 整数解的个数可以构成一个首先为4,公差为4的等差数列,则所求为第20项,可计算得结果.
整数解的个数可以构成一个首先为4,公差为4的等差数列,则所求为第20项,可计算得结果.
6.小波一星期的 总开支分布图如图1所示,一星期的食品开支如图2所示,则小波一星期的鸡蛋开支占总开支的百分比为
总开支分布图如图1所示,一星期的食品开支如图2所示,则小波一星期的鸡蛋开支占总开支的百分比为
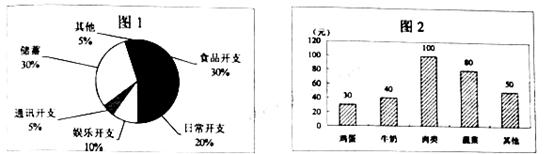
A.30% B.10% C.3% D.不能确定
【答案】C
【解析】本题是一个读图题,图形看懂结果很容易计算.
7.若一个几何体的三视图如图所示,则此几何体的体积为
【答案】C
【解析】本题的主视图是一个六棱柱,由三视图可得地面为变长为1的正六边形,高为1,则直接带公式可求.
8.椭圆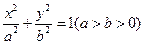 的左、右顶点分别是A,B,左、右焦点分别是F1,F2。若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为
的左、右顶点分别是A,B,左、右焦点分别是F1,F2。若|AF1|,|F1F2|,|F1B|成等比数列,则此椭圆的离心率为
【答案】C
【解析】本题主要考查椭圆和等比数列的知识,根据等比中项的性质可得结果.
9.已知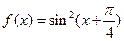 若a=f(lg5),
若a=f(lg5),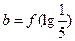 则
则
A.a+b=0 B.a-b=0 C.a+b=1 D.a-b=1
【答案】C
【解析】本题可采用降幂 处理,则
处理,则
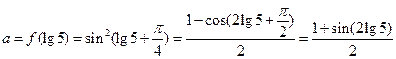
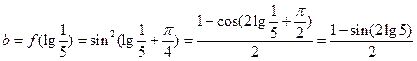 ,则可得a+b=1.
,则可得a+b=1.
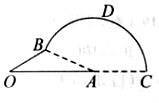
10.如右图,OA=2(单位:m),OB=1(单位:m),OA与OB的夹角为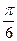 ,以A为圆心,AB为半径作圆弧
,以A为圆心,AB为半径作圆弧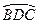 与线段OA延长线交与点C.甲。乙两质点同时从点O出发,甲先以速度1(单位:ms)沿线段OB行至点B,再以速度3(单位:ms)沿圆弧
与线段OA延长线交与点C.甲。乙两质点同时从点O出发,甲先以速度1(单位:ms)沿线段OB行至点B,再以速度3(单位:ms)沿圆弧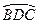 行至点C后停止,乙以速率2(单位:m/s)沿线段OA行至A点后停止。设t时刻甲、乙所到的两点连线与它们经过的路径所围成图形的面积为S(t)(S(0)=0),则函数y=S(t)的图像大致是
行至点C后停止,乙以速率2(单位:m/s)沿线段OA行至A点后停止。设t时刻甲、乙所到的两点连线与它们经过的路径所围成图形的面积为S(t)(S(0)=0),则函数y=S(t)的图像大致是
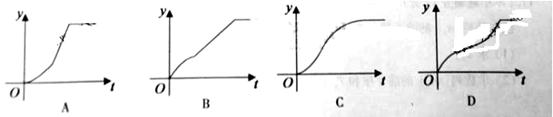
【答案】A
第Ⅱ卷
二。填空题:本大题共5小题,每小题5分,共25分。
【答案】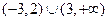
【解析】不等式可化为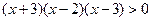 采用穿针引线法解不等式即可.
采用穿针引线法解不等式即可.
12.设单位向量m=(x,y),b=(2,-1)。若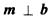 ,则
,则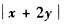 =_______________
=_______________
【答案】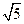
【解析】由已知可得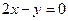 ,又因为m为单位向量所以
,又因为m为单位向量所以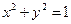 ,联立解得
,联立解得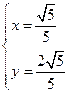 或
或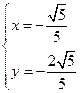 代入所求即可.
代入所求即可.
13.等比数列{an}的前n项和为Sn,公比不为1。若a1=1,且对任意的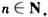 都有an+2+an+1-2an=0,则S5=_________________。
都有an+2+an+1-2an=0,则S5=_________________。
【答案】11
【解析】由已知可得公比q=-2,则a1=1可得S5。
14.过直线x+y-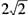 =0上点P作圆x2+y2=1的两条切线,若两条切
=0上点P作圆x2+y2=1的两条切线,若两条切 线的夹角是60°,则点P的坐标是__________。
线的夹角是60°,则点P的坐标是__________。
【答案】(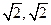 )
)
【解析】本题主要考查数形结合的思想,设p(x,y),则由已知可得po(0为原点)与切线的夹角为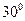 ,则|po|=2,由
,则|po|=2,由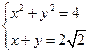 可得
可得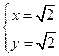 .
.
15.下图是某算法的程序框图,则程序运行后输入的结果是_________。

【答案】3
【解析】当k=1,a=1,T=1
当k=2,a=0,T=1
当k=3,a=0,T=1
当k=4,a=1,T=2
当k=5,a=1,T=3,则此时k=k+1=6所以输出T=3.
三、解答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤。
16.(本小题满分12分)
△ABC中,角A,B,C的对边分别为a,b,c。已知3cos(B-C)-1=6cosBcosC。
(1)求cosA;
【解析】(1)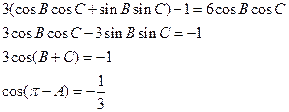 则
则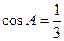 .
.
(2) 由(1)得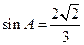 ,由面积可得bc=6①,则根据余弦定理
,由面积可得bc=6①,则根据余弦定理
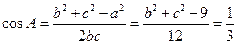 则
则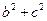 =13②,①②
=13②,①② 两式联立可得b=1,c=5或b=5,c=1.
两式联立可得b=1,c=5或b=5,c=1.
17.(本小题满分12分)
已知数列|an|的前n项和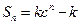 (其中c
(其中c ,k为常数),且a2=4,a6=8a3
,k为常数),且a2=4,a6=8a3
(1)求an;
(2)求数列{nan}的前n项和Tn。
【解析】(1)当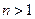 时,
时,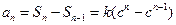
则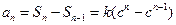
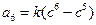 ,
,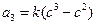
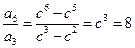 ,∴c=2.∵a2=4,即
,∴c=2.∵a2=4,即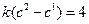 ,解得k=2,∴
,解得k=2,∴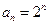 (n)1)
(n)1)
当n=1时,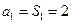
综上所述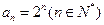
(2) 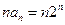 ,则
,则
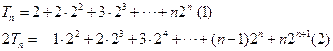 (1)-(2)得
(1)-(2)得
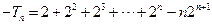
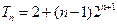
18.(本小题满分12分)
如图,从A1(1,0,0),A2(2,0,0),B1(0,1,0,)B2(0,2,0),C1(0,0,1),C2(0,0,2)这6个点中随机选取3个点。
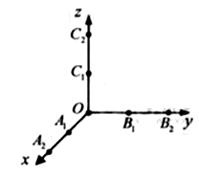
(1) 求这3点与原点O恰好是正三棱锥的四个顶点的概率;
(2) 求这3点与原点O共面的概率。
【解析】(1)总的结果数为20种,则满足条件的种数为2种所以所求概率为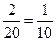
(2)满足条件的情况为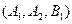 ,
,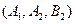 ,
,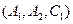 ,
,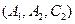 ,
,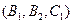 ,
,
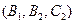 ,所以所求概率为
,所以所求概率为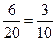 .
.
19. (本小题满分12分)
如图,在梯形ABCD中,AB∥CD,E,F是线段AB上的两点,且DE⊥AB,CF⊥AB,AB=12,AD=5,BC=4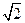 ,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.
,DE=4.现将△ADE,△CFB分别沿DE,CF折起,使A,B两点重合与点G,得到多面体CDEFG.
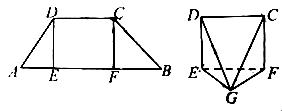
(1) 求证:平面DEG⊥平面CFG;
(2)  求多面体C
求多面体C DEFG的体积。
DEFG的体积。
【解析】(1)由已知可得AE=3,BF=4,则折叠完后EG=3,GF=4,又因为EF=5,所以可得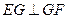
又因为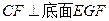 ,可得
,可得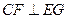 ,即
,即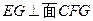 所以平面DEG⊥平面CFG.
所以平面DEG⊥平面CFG.
(2)过G作GO垂直于EF,GO 即为四棱锥G-EFCD的高,所以所求体积为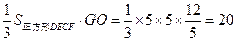
20.(本小题满分13分)
已知三点O(0,0),A(-2,1) ,B(2,1),曲线C上任意一点M(x,y)满足
,B(2,1),曲线C上任意一点M(x,y)满足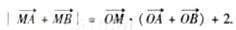
(1)求曲线C的方程;
(2)点Q(x0,y0)(-2<x0<2)是曲线C上动点,曲线C在点Q处的切线为l,点P的坐标是(0,-1),l与PA,PB分别交于点D,E,求△QAB与△PDE的面积之比。
 【解析】(1)
【解析】(1)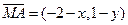 ,
,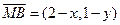 ,
,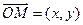 ,
,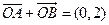
代入式子可得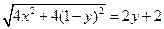 整理得
整理得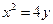
(2)
21.(本小题满分14分)
已知函数f(x)=(ax2+bx+c)ex在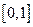 上单调递减且满足f(0)=1,f(1)=0.
上单调递减且满足f(0)=1,f(1)=0.
(1)求a的取值范围;
(2)设g(x)= f(-x)- f′(x),求g(x)在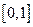 上的最大值和最小值。
上的最大值和最小值。
【解析】(1)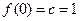 ,
,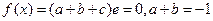 ,
,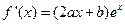 因为在[0,1]上单调递减则令
因为在[0,1]上单调递减则令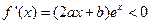 即
即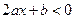 解得
解得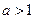
(2)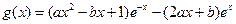
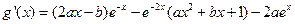

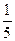 B.3 C.
B.3 C. 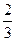
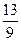
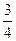 B.
B. 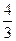 D.
D. 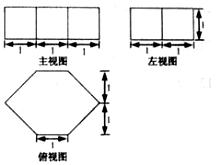
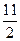 B.5 C.4 D.
B.5 C.4 D. 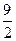
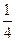 B.
B. 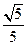
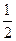 D.
D.