(单词翻译:单击)
一.选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若复数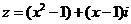 为纯虚数,则实数
为纯虚数,则实数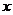 的值为
的值为
A.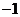 B.
B.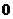 C.
C.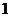 D.
D.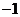 或
或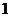
答案:A
【解析】由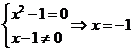 故选A
故选A
2.函数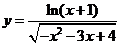 的定义域为
的定义域为
A.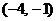 B.
B.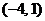 C.
C.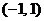 D.
D.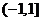
答案:C
【解析】由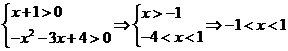 .故选C
.故选C
3.已知全集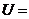
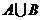 中有m个元素,
中有m个元素,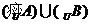 中有n个元素.若
中有n个元素.若 非空,则
非空,则 的元素个数为
的元素个数为
A.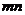 B.
B.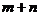 C.
C.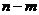 D.
D.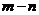
答案:D
【解析】因为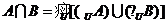 ,所以
,所以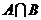 共有
共有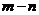 个元素,故选D
个元素,故选D
4.若函数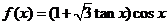 ,
,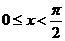 ,则
,则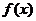 的最大值为
的最大值为
A.1 B.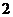 C.
C.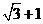 D.
D.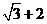
答案:B
【解析】因为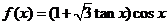 =
=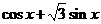 =
=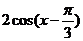
当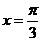 是,函数取得最大值为2. 故选B
是,函数取得最大值为2. 故选B
5.设函数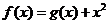 ,曲线
,曲线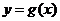 在点
在点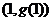 处的切线方程为
处的切线方程为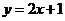 ,则曲线
,则曲线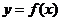 在点
在点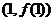 处切线的斜率为
处切线的斜率为
A.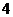 B.
B.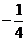 C.
C.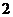 D.
D.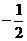
答案:A
【解析】由已知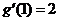 ,而
,而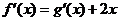 ,所以
,所以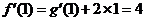 故选A
故选A
6.过椭圆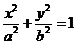 (
(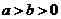 )的左焦点
)的左焦点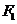 作
作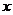 轴的垂线交椭圆于点
轴的垂线交椭圆于点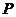 ,
,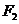 为右焦点,若
为右焦点,若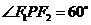 ,则椭圆的离心率为
,则椭圆的离心率为
A.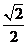 B.
B.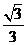 C.
C.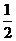 D.
D.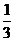

答案:B
【解析】因为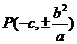 ,再由
,再由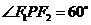 有
有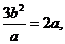 从而可得
从而可得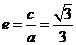 ,故选B
,故选B
7.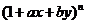 展开式中不含
展开式中不含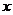 的项的系数绝对值的和为
的项的系数绝对值的和为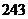 ,不含
,不含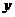 的项的系数绝对值的和为
的项的系数绝对值的和为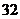 ,则
,则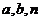 的值可能为
的值可能为
A.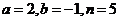 B.
B.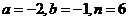
C.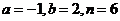 D.
D.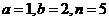

答案:D
【解析】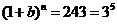 ,
,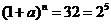 ,则可取
,则可取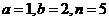 ,选D
,选D
8.数列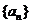 的通项
的通项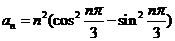 ,其前
,其前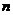 项和为
项和为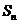 ,则
,则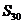 为
为
A.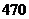 B.
B.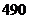 C.
C. D.
D.
答案:A
【解析】由于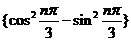 以3 为周期,故
以3 为周期,故
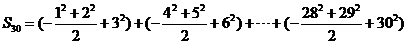
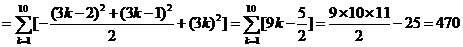 故选A
故选A
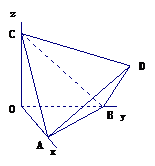
9.如图,正四面体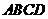 的顶点
的顶点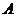 ,
,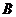 ,
,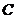 分别在两两垂直的三条射线
分别在两两垂直的三条射线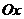 ,
,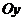 ,
,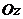 上,则在下列命题中,错误的为
上,则在下列命题中,错误的为
A.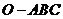 是正三棱锥
是正三棱锥
B.直线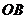 ∥平面
∥平面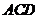
C.直线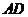 与
与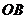 所成的角是
所成的角是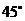
D.二面角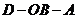 为
为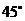
答案:B
【解析】将原图补为正方体不难得出B为错误,故选B
10.为了庆祝六一儿童节,某食品厂制作了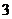 种不同的精美卡片,每袋食品随机装入一张卡片,集齐
种不同的精美卡片,每袋食品随机装入一张卡片,集齐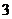 种卡片可获奖,现购买该种食品
种卡片可获奖,现购买该种食品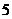 袋,能获奖的概率为
袋,能获奖的概率为
A.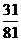 B.
B.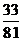 C.
C.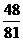 D.
D.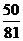

答案:D
【解析】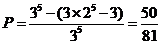 故选D
故选D
11.一个平面封闭区域内任意两点距离的最大值称为该区域的“直径”,封闭区域边界曲线的长度与区域直径之比称为区域的“周率”,下面四个平面区域(阴影部分)的周率从左到右依次记为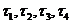 ,则下列关系中正确的为
,则下列关系中正确的为
 |
A.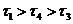 B.
B.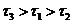 C.
C.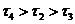 D.
D.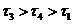
答案:C
【解析】前三个区域的周率依次等于正方形、圆、正三角形的周长和最远距离,所以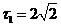 、
、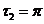 、
、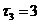 ,第四个区域的周率可以转化为一个正六边形的周长与它的一对平行边之间的距离之比,所以
,第四个区域的周率可以转化为一个正六边形的周长与它的一对平行边之间的距离之比,所以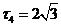 ,则
,则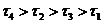 ,选C
,选C
12.设函数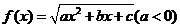 的定义域为
的定义域为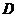 ,若所有点
,若所有点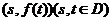 构成一个正方形区域,则
构成一个正方形区域,则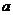 的值为
的值为
A.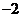 B.
B.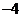 C.
C.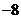 D.不能确定
D.不能确定

答案:B
【解析】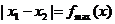 ,
,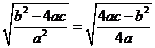 ,
,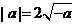 ,
,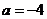 ,选B
,选B
第Ⅱ卷
二.填空题:本大题共4小题,每小题4分,共16分。请把答案填在答题卡上
13.已知向量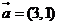 ,
,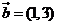 ,
,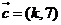 ,若
,若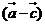 ∥
∥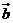 ,则
,则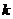 =__________.
=__________.
答案: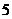
【解析】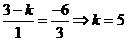
14.正三棱柱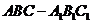 内接于半径为
内接于半径为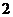 的球,若
的球,若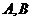 两点的球面距离为
两点的球面距离为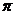 ,则正三棱柱的体积为 .
,则正三棱柱的体积为 .
答案: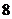
【解析】由条件可得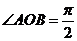 ,所以
,所以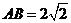 ,
,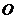 到平面
到平面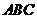 的距离为
的距离为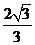 ,所以所求体积等于
,所以所求体积等于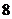 .
.
15.若不等式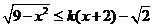 的解集为区间
的解集为区间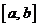 ,且
,且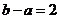 ,则
,则 .
.
答案: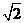
【解析】由数形结合,直线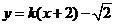 在半圆
在半圆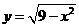 之下必须
之下必须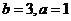 ,则直线
,则直线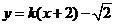 过点(
过点(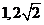 ),则
),则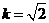
16.设直线系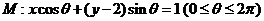 ,对于下列四个命题:
,对于下列四个命题:
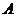 .
.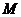 中所有直线均经过一个定点
中所有直线均经过一个定点
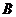 .存在定点
.存在定点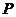 不在
不在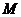 中的任一条直线上
中的任一条直线上
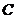 .对于任意整数
.对于任意整数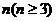 ,存在正
,存在正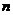 边形,其所有边均在
边形,其所有边均在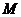 中的直线上
中的直线上
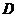 .
.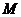 中的直线所能围成的正三角形面积都相等
中的直线所能围成的正三角形面积都相等
其中真命题的代号是 (写出所有真命题的代号).
答案: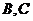
【解析】因为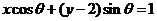 所以点
所以点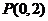 到
到 中每条直线的距离
中每条直线的距离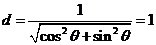
即 为圆
为圆 :
: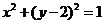 的全体切线组成的集合,从而
的全体切线组成的集合,从而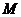 中存在两条平行直线,所以A错误
中存在两条平行直线,所以A错误
又因为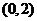 点不存在任何直线上,所以B正确
点不存在任何直线上,所以B正确
对任意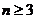 ,存在正
,存在正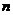 边形使其内切圆为圆
边形使其内切圆为圆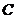 ,故
,故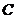 正确
正确
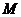 中边能组成两个大小不同的正三角形
中边能组成两个大小不同的正三角形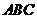 和
和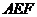 ,故D错误,
,故D错误,
故命题中正确的序号是 B,C
三.解答题:本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤
17.(本小题满分12分)
设函数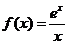
(1)求函数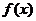 的单调区间;
的单调区间;
(2)若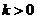 ,求不等式
,求不等式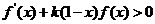 的解集.
的解集.
解: (1) 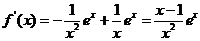 , 由
, 由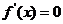 ,得
,得 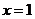 .
.
因为 当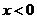 时,
时,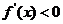 ; 当
; 当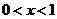 时,
时,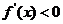 ; 当
; 当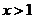 时,
时,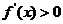 ;
;
所以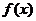 的单调增区间是:
的单调增区间是: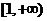 ; 单调减区间是:
; 单调减区间是: 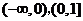 .
.
(2) 由 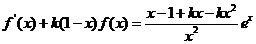
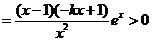 ,
,
得: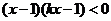 .
.
故:当 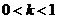 时, 解集是:
时, 解集是: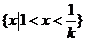 ;
;
当 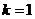 时,解集是:
时,解集是: 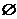 ;
;
当 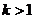 时, 解集是:
时, 解集是: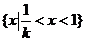 .
.
18.(本小题满分12分)
某公司拟资助三位大学生自主创业,现聘请两位专家,独立地对每位大学生的创业方案进行评审.假设评审结果为“支持”或“不支持”的概率都是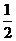 .若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令
.若某人获得两个“支持”,则给予10万元的创业资助;若只获得一个“支持”,则给予5万元的资助;若未获得“支持”,则不予资助,令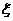 表示该公司的资助总额.
表示该公司的资助总额.
(1) 写出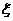 的分布列; (2) 求数学期望
的分布列; (2) 求数学期望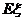
解:(1)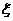 的所有取值为
的所有取值为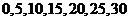
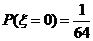
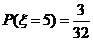
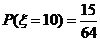
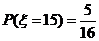
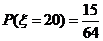
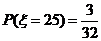
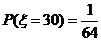
(2)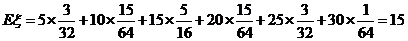 .
.
19.(本小题满分12分)
△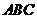 中,
中,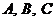 所对的边分别为
所对的边分别为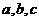 ,
,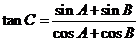 ,
,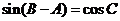 .
.
(1)求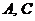 ;
;
(2)若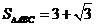 ,求
,求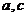 .
. 
解:(1) 因为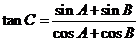 ,即
,即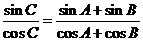 ,
,
所以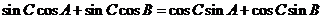 ,
,
即 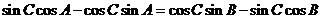 ,
,
得 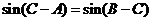 . 所以
. 所以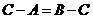 ,或
,或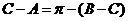 (不成立).
(不成立).
即 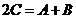 , 得
, 得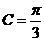 ,所以.
,所以.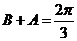
又因为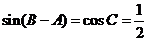 ,则
,则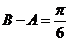 ,或
,或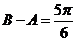 (舍去)
(舍去)
得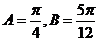
(2)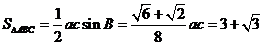 ,
,
又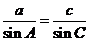 , 即
, 即 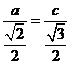 ,
,
得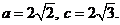
20.(本小题满分12分)
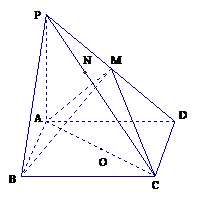
在四棱锥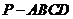 中,底面
中,底面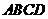 是矩形,
是矩形,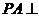 平面
平面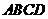 ,
,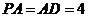 ,
,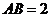 . 以
. 以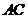 的中点
的中点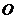 为球心、
为球心、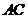 为直径的球面交
为直径的球面交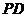 于点
于点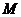 ,交
,交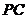 于点
于点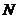 .
.
(1)求证:平面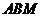 ⊥平面
⊥平面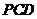 ;
; 
(2)求直线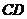 与平面
与平面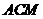 所成的角的大小;
所成的角的大小;
(3)求点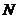 到平面
到平面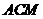 的距离.
的距离.
解:
方法一:(1)依题设知,AC是所作球面的直径,则AM⊥MC。
又因为P A⊥平面ABCD,则PA⊥CD,又CD⊥AD,
所以CD⊥平面PAD,则CD⊥AM,所以A M⊥平面PCD,
所以平面ABM⊥平面PCD。
(2)由(1)知,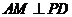 ,又
,又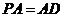 ,则
,则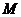 是
是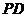 的中点可得
的中点可得
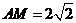 ,
,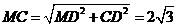
则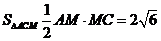
设D到平面ACM的距离为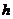 ,由
,由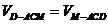 即
即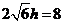 ,
,
可求得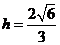 ,
,
设所求角为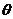 ,则
,则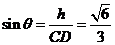 ,
,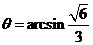 。
。
(3) 可求得PC=6。因为AN⊥NC,由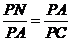 ,得PN
,得PN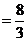 。所以
。所以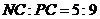 。
。
故N点到平面ACM的距离等于P点到平面ACM距离的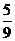 。
。
又因为M是PD的中点,则P、D到平面ACM的距离相等,由(2)可知所求距离为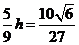 。
。
方法二:
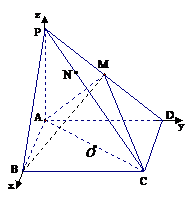
(1)同方法一;
(2)如图所示,建立空间直角坐标系,则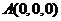 ,
,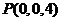 ,
,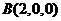 ,
, 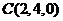 ,
,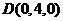 ,
,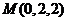 ;设平面
;设平面 的一个法向量
的一个法向量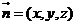 ,由
,由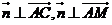 可得:
可得: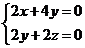 ,令
,令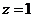 ,则
,则
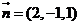 。设所求角为
。设所求角为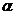 ,则
,则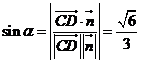 ,
,
所以所求角的大小为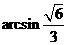 。
。
(3)由条件可得,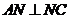 .在
.在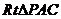 中,
中,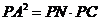 ,所以
,所以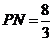 ,则
,则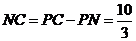 ,
, 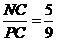 ,所以所求距离等于点
,所以所求距离等于点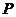 到平面
到平面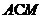 距离的
距离的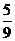 ,设点
,设点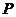 到平面
到平面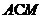 距离为
距离为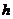 则
则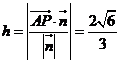 ,所以所求距离为
,所以所求距离为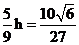 。
。
21.(本小题满分12分)
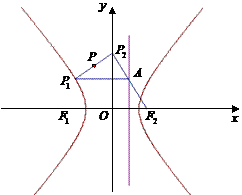
已知点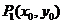 为双曲线
为双曲线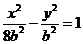 (
(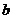 为正常数)上任一点,
为正常数)上任一点,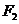 为双曲线的右焦点,过
为双曲线的右焦点,过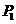 作右准线的垂线,垂足为
作右准线的垂线,垂足为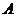 ,连接
,连接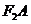 并延长交
并延长交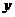 轴于
轴于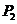 .
.
(1) 求线段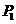
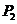 的中点
的中点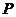 的轨迹
的轨迹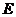 的方程;
的方程;
(2) 设轨迹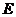 与
与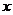 轴交于
轴交于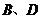 两点,在
两点,在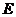 上任取一点
上任取一点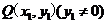 ,直线
,直线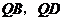 分别交
分别交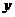 轴于
轴于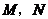 两点.求证:以
两点.求证:以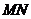 为直径的圆过两定点.
为直径的圆过两定点.
解: (1) 由已知得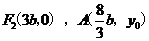 ,则直线
,则直线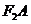 的方程为:
的方程为: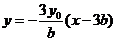 ,
,
令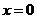 得
得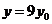 ,即
,即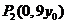 ,
,
设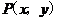 ,则
,则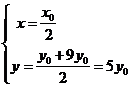 ,即
,即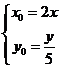 代入
代入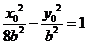 得:
得: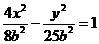 ,
,
即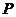 的轨迹
的轨迹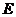 的方程为
的方程为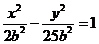 .
.
(2) 在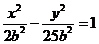 中令
中令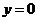 得
得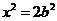 ,则不妨设
,则不妨设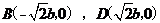 ,
,
于是直线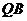 的方程为:
的方程为: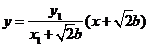 ,
, 直线
直线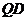 的方程为:
的方程为: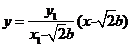 ,
,
则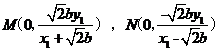 ,
,
则以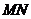 为直径的圆的方程为:
为直径的圆的方程为: 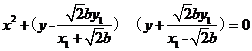
 ,
,
令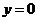 得:
得: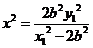 ,而
,而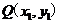 在
在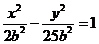 上,则
上,则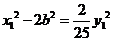 ,
,
于是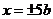 ,即以
,即以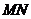 为直径的圆过两定点
为直径的圆过两定点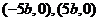 .
.
22.(本小题满分14分)
各项均为正数的数列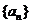 ,
,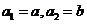 ,且对满足
,且对满足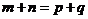 的正整数
的正整数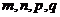 都有
都有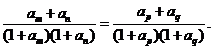
(1)当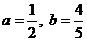 时,求通项
时,求通项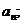
(2)证明:对任意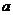 ,存在与
,存在与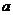 有关的常数
有关的常数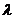 ,使得对于每个正整数
,使得对于每个正整数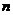 ,都有
,都有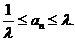
解:(1)由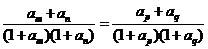 得
得
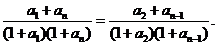 将
将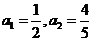 代入化简得
代入化简得
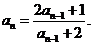
所以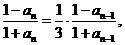
故数列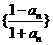 为等比数列,从而
为等比数列,从而
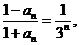 即
即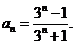
可验证,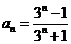 满足题设条件.
满足题设条件.
(2) 由题设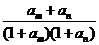 的值仅与
的值仅与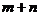 有关,记为
有关,记为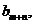 则
则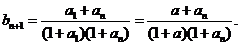
考察函数 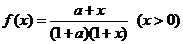 ,则在定义域上有
,则在定义域上有
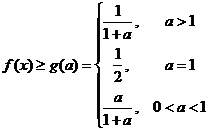
故对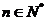 ,
, 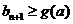 恒成立.
恒成立.
又 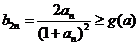 ,
,
注意到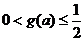 ,解上式得
,解上式得
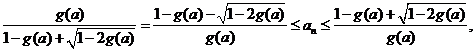
取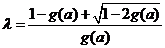 ,即有
,即有 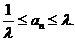 .
.