(单词翻译:单击)
一、选择题:
1.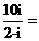
A.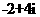 B.
B.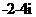 C.
C.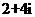 D.
D.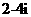
解:原式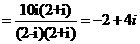 .故选A.
.故选A.
2. 设集合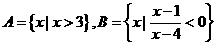 ,则
,则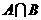 =
=
A.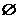 B.
B.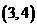 C.
C.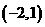 D.
D.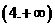
解: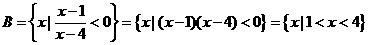 .
.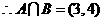 .故选B.
.故选B.
3. 已知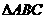 中,
中,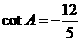 , 则
, 则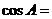
A.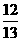 B.
B.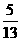 C.
C.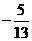 D.
D.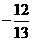
解:已知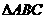 中,
中,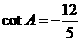 ,
,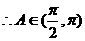 .
.
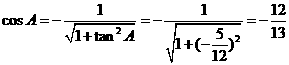 故选D.
故选D.
4.曲线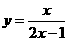 在点
在点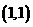 处的切线方程为
处的切线方程为 
A.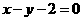 B.
B.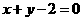 C.
C.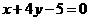 D.
D.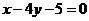
解: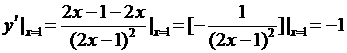 ,
,
故切线方程为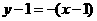 ,即
,即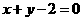 故选B.
故选B.
5. 已知正四棱柱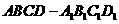 中,
中,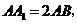
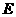 为
为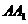 中点,则异面直线
中点,则异面直线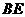 与
与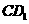 所成的角的余弦值为
所成的角的余弦值为
A.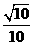 B.
B.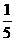 C.
C.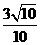 D.
D.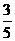
解:令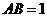 则
则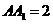 ,连
,连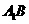
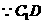 ∥
∥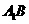
 异面直线
异面直线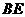 与
与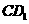 所成的角即
所成的角即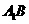
与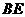 所成的角。在
所成的角。在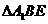 中由余弦定理易得
中由余弦定理易得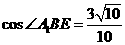 。故选C
。故选C
6. 已知向量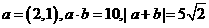 ,则
,则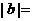

A.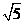 B.
B.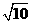 C.
C.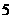 D.
D.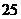
解: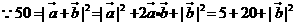
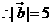 。故选C
。故选C
7. 设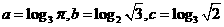 ,则
,则
A.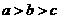 B.
B.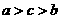 C.
C.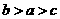 D.
D.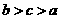
解: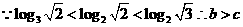
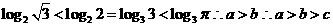 .故选A.
.故选A.
8. 若将函数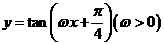 的图像向右平移
的图像向右平移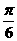 个单位长度后,与函数
个单位长度后,与函数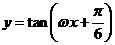 的图像重合,则
的图像重合,则 的最小值为
的最小值为
A.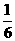 B.
B.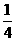 C.
C.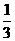 D.
D.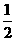
解: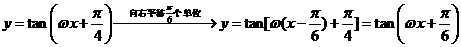
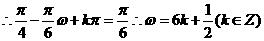 ,
,
又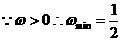 .故选D
.故选D
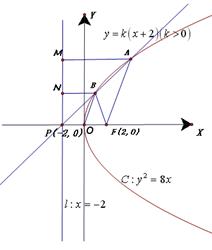
9. 已知直线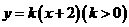 与抛物线
与抛物线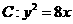 相交于
相交于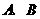 两点,
两点,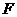 为
为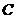 的焦点,若
的焦点,若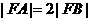 ,则
,则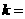
A.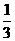 B.
B.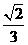 C.
C.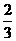 D.
D.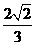
解:设抛物线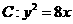 的准线为
的准线为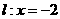 直线
直线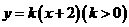 恒过定点P
恒过定点P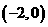 .如图过
.如图过 分 别作
分 别作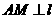 于
于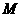 ,
,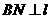 于
于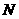 , 由
, 由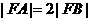 ,则
,则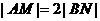 ,点B为AP的中点.连结
,点B为AP的中点.连结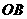 ,则
,则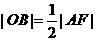 ,
,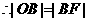 点
点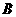 的横坐标为
的横坐标为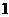 , 故点
, 故点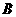 的坐标为
的坐标为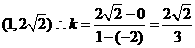 , 故选D
, 故选D
10. 甲、乙两人从4门课程中各选修2门。则甲、乙所选的课程中至少有1门不相同的选法共有
A. 6种 B. 12种 C. 30种 D. 36种
解:用间接法即可.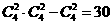 种. 故选C
种. 故选C
11. 已知双曲线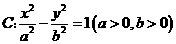 的右焦点为
的右焦点为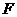 ,过
,过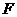 且斜率为
且斜率为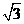 的直线交
的直线交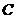 于
于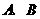 两点,若
两点,若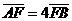 ,则
,则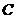 的离心率为
的离心率为
A.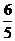 B.
B.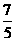 C.
C.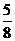 D.
D.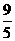
解:设双曲线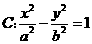 的右准线为
的右准线为 ,过
,过 分 别作
分 别作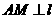 于
于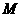 ,
,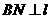 于
于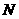 ,
,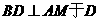 ,由直线AB的斜率为
,由直线AB的斜率为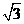 ,知直线AB的倾斜角为
,知直线AB的倾斜角为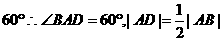 ,
,
由双曲线的第二定义有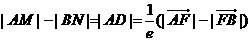
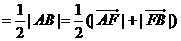 .
.
又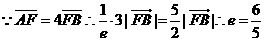 故选A
故选A
12.纸制的正方体的六个面根据其方位分别标记为上、下、东、南、西、北。现有沿该正方体的一些棱将正方体剪开、外面朝上展平,得到右侧的平面图形,则标“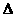 ”的面的方位是
”的面的方位是
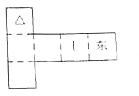
A. 南 B. 北
C. 西 D. 下
解:展、折问题。易判断选B
第II卷(非选择题,共90分)
二、填空题:本大题共4小题,每小题5分,共20分。把答案填在答题卡上。
13.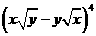 的展开式中
的展开式中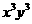 的系数为 6 。
的系数为 6 。
解: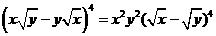 ,只需求
,只需求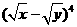 展开式中的含
展开式中的含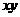 项的系数:
项的系数: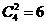

14. 设等差数列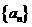 的前
的前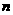 项和为
项和为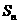 ,若
,若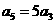 则
则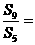 9 .
9 .
解: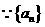 为等差数列,
为等差数列,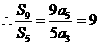
15.设 是球
是球 的半径,
的半径,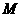 是
是 的中点,过
的中点,过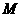 且与
且与 成45°角的平面截球
成45°角的平面截球 的表面得到圆
的表面得到圆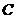 。若圆
。若圆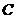 的面积等于
的面积等于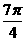 ,则球
,则球 的表面积等于
的表面积等于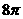 .
.
解:设球半径为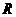 ,圆
,圆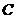 的半径为
的半径为 ,
,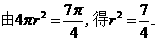
因为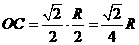 。由
。由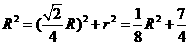 得
得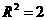 .故球
.故球 的表面积等于
的表面积等于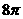 .
.
16. 已知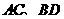 为圆
为圆 :
: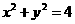 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为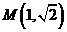 ,则四边形
,则四边形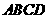 的面积的最大值为 。
的面积的最大值为 。
解:设圆心 到
到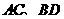 的距离分别为
的距离分别为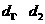 ,则
,则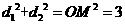 .
.
四边形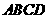 的面积
的面积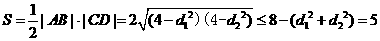
三、解答题:本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤
17(本小题满分10分)
设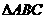 的内角
的内角 、
、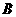 、
、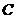 的对边长分别为
的对边长分别为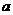 、
、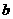 、
、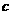 ,
,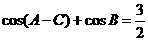 ,
,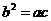 ,求
,求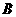 。
。
分析:由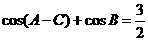 ,易想到先将
,易想到先将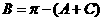 代入
代入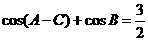 得
得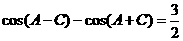 。然后利用两角和与差的余弦公式展开得
。然后利用两角和与差的余弦公式展开得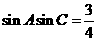 ;又由
;又由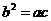 ,利用正弦定理进行边角互化,得
,利用正弦定理进行边角互化,得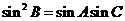 ,进而得
,进而得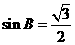 .故
.故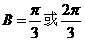 。大部分考生做到这里忽略了检验,事实上,当
。大部分考生做到这里忽略了检验,事实上,当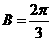 时,由
时,由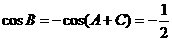 ,进而得
,进而得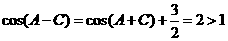 ,矛盾,应舍去。
,矛盾,应舍去。
也可利用若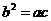 则
则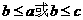 从而舍去
从而舍去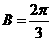 。不过这种方法学生不易想到。
。不过这种方法学生不易想到。
评析:本小题考生得分易,但得满分难。
18(本小题满分12分)
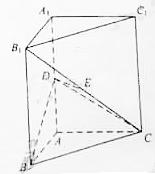
如图,直三棱柱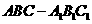 中,
中,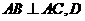 、
、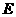 分别为
分别为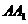 、
、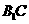 的中点,
的中点,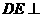 平面
平面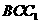
(I)证明: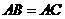
(II)设二面角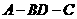 为60°,求
为60°,求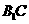 与平面
与平面 所成的角的大小。
所成的角的大小。
(I)分析一:连结BE,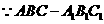 为直三棱柱,
为直三棱柱,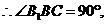
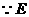 为
为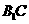 的中点,
的中点,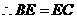 。又
。又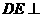 平面
平面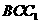 ,
,
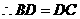 (射影相等的两条斜线段相等)而
(射影相等的两条斜线段相等)而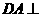 平面
平面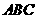 ,
,
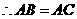 (相等的斜线段的射影相等)。
(相等的斜线段的射影相等)。
分析二:取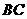 的中点
的中点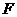 ,证四边形
,证四边形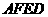 为平行四边形,进而证
为平行四边形,进而证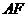 ∥
∥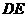 ,
,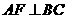 ,得
,得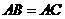 也可。
也可。
分析三:利用空间向量的方法。具体解法略。
(II)分析一:求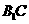 与平面
与平面 所成的线面角,只需求点
所成的线面角,只需求点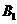 到面
到面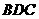 的距离即可。
的距离即可。

作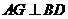 于
于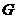 ,连
,连 ,则
,则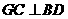 ,
, 为二面角
为二面角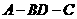 的平面角,
的平面角,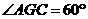 .不妨设
.不妨设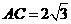 ,则
,则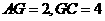 .在
.在 中,由
中,由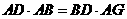 ,易得
,易得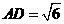 .
.
设点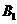 到面
到面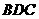 的距离为
的距离为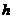 ,
,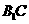 与平面
与平面 所成的角为
所成的角为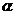 。利用
。利用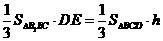 ,可求得
,可求得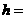
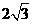 ,又可求得
,又可求得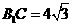
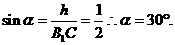
即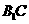 与平面
与平面 所成的角为
所成的角为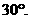
分析二:作出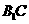 与平面
与平面 所成的角再行求解。如图可证得
所成的角再行求解。如图可证得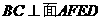 ,所以面
,所以面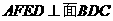 。由分析一易知:四边形
。由分析一易知:四边形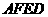 为正方形,连
为正方形,连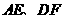 ,并设交点为
,并设交点为 ,则
,则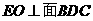 ,
, 为
为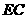 在面
在面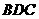 内的射影。
内的射影。 。以下略。
。以下略。
分析三:利用空间向量的方法求出面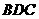 的法向量
的法向量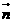 ,则
,则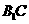 与平面
与平面 所成的角即为
所成的角即为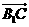 与法向量
与法向量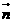 的夹角的余角。具体解法详见高考试题参考答案。
的夹角的余角。具体解法详见高考试题参考答案。
总之在目前,立体几何中的两种主要的处理方法:传统方法与向量的方法仍处于各自半壁江山的状况。命题人在这里一定会兼顾双方的利益。
19(本小题满分12分)
设数列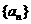 的前
的前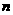 项和为
项和为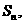 已知
已知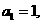
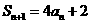
(I)设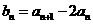 ,证明数列
,证明数列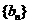 是等比数列
是等比数列
(II)求数列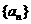 的通项公式。
的通项公式。
解:(I)由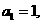 及
及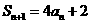 ,有
,有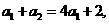
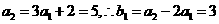
由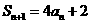 ,...① 则当
,...① 则当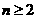 时,有
时,有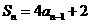 .....②
.....②
②-①得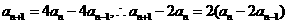
又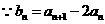 ,
,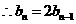
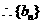 是首项
是首项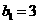 ,公比为2的等比数列.
,公比为2的等比数列.
(II)由(I)可得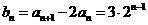 ,
,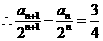
 数列
数列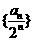 是首项为
是首项为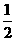 ,公差为
,公差为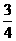 的等比数列.
的等比数列.

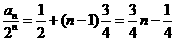 ,
,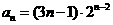
评析:第(I)问思路明确,只需利用已知条件寻找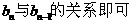 .
.
第(II)问中由(I)易得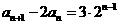 ,这个递推式明显是一个构造新数列的模型:
,这个递推式明显是一个构造新数列的模型: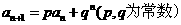 ,主要的处理手段是两边除以
,主要的处理手段是两边除以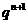 .
.
20(本小题满分12分)
某车间甲组有10名工人,其中有4名女工人;乙组有5名工人,其中有3名女工人,现采用分层抽样方法(层内采用不放回简单随机抽样)从甲、乙两组中共抽取3名工人进行技术考核。
(I)求从甲、乙两组各抽取的人数;
(II)求从甲组抽取的工人中恰有1名女工人的概率;
(III)记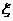 表示抽取的3名工人中男工人数,求
表示抽取的3名工人中男工人数,求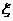 的分布列及数学期望。
的分布列及数学期望。
分析:(I)这一问较简单,关键是把握题意,理解分层抽样的原理即可。另外要注意此分层抽样与性别无关。
(II)在第一问的基础上,这一问处理起来也并不困难。
从甲组抽取的工人中恰有1名女工人的概率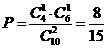
(III)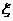 的可能取值为0,1,2,3
的可能取值为0,1,2,3
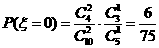 ,
,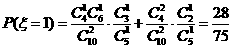 ,
,
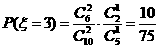 ,
,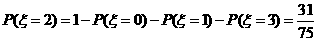
分布列及期望略。
评析:本题较常规,比08年的概率统计题要容易。在计算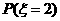 时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
时,采用分类的方法,用直接法也可,但较繁琐,考生应增强灵活变通的能力。
(21)(本小题满分12分)
已知椭圆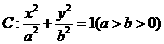 的离心率为
的离心率为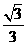 ,过右焦点F的直线
,过右焦点F的直线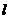 与
与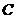 相交于
相交于 、
、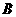 两点,当
两点,当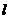 的斜率为1时,坐标原点
的斜率为1时,坐标原点 到
到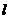 的距离为
的距离为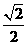
(I)求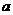 ,
,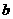 的值;
的值;
(II)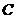 上是否存在点P,使得当
上是否存在点P,使得当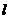 绕F转到某一位置时,有
绕F转到某一位置时,有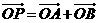 成立?若存在,求出所有的P的坐标与
成立?若存在,求出所有的P的坐标与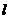 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
解:(I)设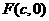 ,直线
,直线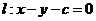 ,由坐标原点
,由坐标原点 到
到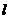 的距离为
的距离为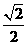
则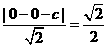 ,解得
,解得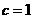 .又
.又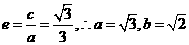 .
.
(II)由(I)知椭圆的方程为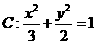 .设
.设 、
、
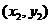
由题意知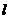 的斜率为一定不为0,故不妨设
的斜率为一定不为0,故不妨设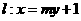
代入椭圆的方程中整理得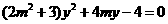 ,显然
,显然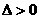 。
。
由韦达定理有: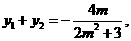
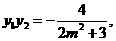 ........①
........①
.假设存在点P,使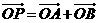 成立,则其充要条件为:
成立,则其充要条件为:
点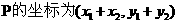 ,点P在椭圆上,即
,点P在椭圆上,即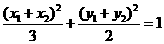 。
。
整理得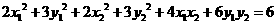 。
。
又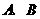 在椭圆上,即
在椭圆上,即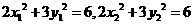 .
.
故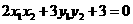 ................................②
................................②
将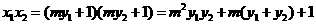 及①代入②解得
及①代入②解得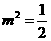
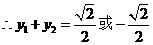 ,
,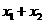 =
=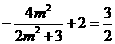 ,即
,即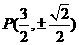 .
.
当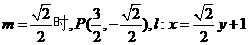 ;
;
当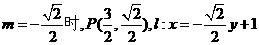 .
.
评析:处理解析几何题,学生主要是在“算”上的功夫不够。所谓“算”,主要讲的是算理和算法。算法是解决问题采用的计算的方法,而算理是采用这种算法的依据和原因,一个是表,一个是里,一个是现象,一个是本质。有时候算理和算法并不是截然区分的。例如:三角形的面积是用底乘高的一半还是用两边与夹角的正弦的一半,还是分割成几部分来算?在具体处理的时候,要根据具体问题及题意边做边调整,寻找合适的突破口和切入点。
22.(本小题满分12分)
设函数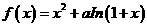 有两个极值点
有两个极值点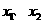 ,且
,且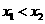
(I)求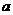 的取值范围,并讨论
的取值范围,并讨论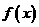 的单调性;
的单调性;
(II)证明: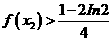
解: (I)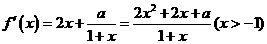
令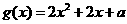 ,其对称轴为
,其对称轴为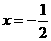 。由题意知
。由题意知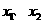 是方程
是方程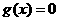 的两个均大于
的两个均大于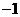 的不相等的实根,其充要条件为
的不相等的实根,其充要条件为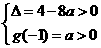 ,得
,得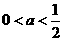
⑴当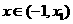 时,
时,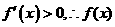 在
在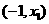 内为增函数;
内为增函数;
⑵当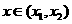 时,
时,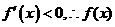 在
在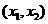 内为减函数;
内为减函数;
⑶当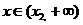 时,
时,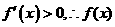 在
在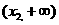 内为增函数;
内为增函数;
(II)由(I)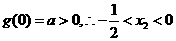 ,
,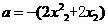
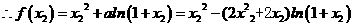
设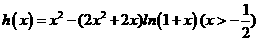 ,
,
则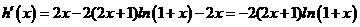
⑴当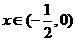 时,
时,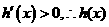 在
在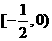 单调递增;
单调递增;
⑵当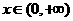 时,
时,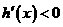 ,
,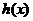 在
在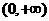 单调递减。
单调递减。
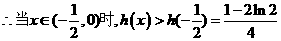
故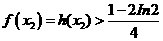 .
.