(单词翻译:单击)
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数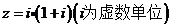 在复平面上对应的点位于
在复平面上对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【答案】 B
【解析】 z = i·(1+i) = i – 1,所以对应点(-1,1).选B
选B
2.某学校有男、女学生各500名.为了解男女学生在学习兴趣与业余爱好方面是否存在显著差异,拟从全体学生中抽取100名学生进行调查,则宜采用的抽样方法是
A.抽签法 B.随机数法 C.系统抽样法 D.分层抽样法
【答案】 D
【解析】 因为抽样的目的与男女性别有关,所以采用分层抽样法能够反映男女人数的比例。
选D
3.在锐角中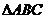 ,角
,角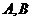 所对的边长分别为
所对的边长分别为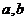 .若
.若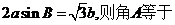
A.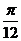 B.
B.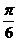 C.
C.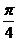 D.
D.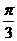
【答案】 D
【解析】 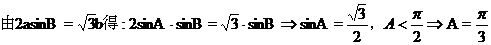
选D
4.若变量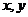 满足约束条件
满足约束条件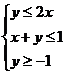 ,
,
A.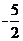 B.
B.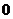 C.
C.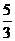 D.
D.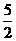
【答案】 C
【解析】 区域为三角形,直线u = x + 2y 经过三角形顶点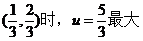
选C
5.函数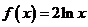 的图像与函数
的图像与函数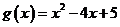 的图像的交点个数为
的图像的交点个数为
A.3 B.2 C.1 D.0
【答案】 B
【解析】 二次函数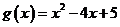 的图像开口向上,在x轴上方,对称轴为x=2,g(2) = 1; f(2) =2ln2=ln4>1.所以g(2) < f(2), 从图像上可知交点个数为2
的图像开口向上,在x轴上方,对称轴为x=2,g(2) = 1; f(2) =2ln2=ln4>1.所以g(2) < f(2), 从图像上可知交点个数为2
选B
6. 已知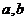 是单位向量,
是单位向量,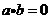 .若向量
.若向量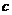 满足
满足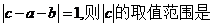
A.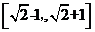 B.
B.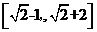
C.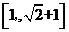 D.
D.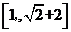
【答案】 A
【解析】 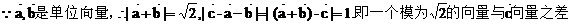 的模为1,可以在单位圆中解得
的模为1,可以在单位圆中解得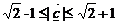 。
。
选A
7.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于
A.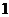 B.
B.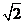 C.
C.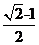 D.
D.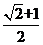
【答案】 C
【解析】 由题知,正方体的棱长为1,
 。
。
选C
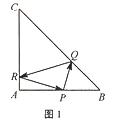 8.在等腰三角形
8.在等腰三角形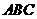 中,
中,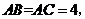 点
点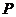 是边
是边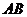 上异于
上异于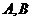 的一点,光线从点
的一点,光线从点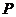 出发,经
出发,经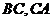 发射后又回到原点
发射后又回到原点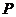 (如图
(如图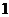 ).若光线
).若光线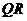 经过
经过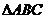 的中心,则
的中心,则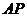 等
等
A.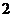 B.
B.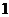
C.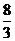 D.
D.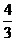
【答案】 D
【解析】 使用解析法。
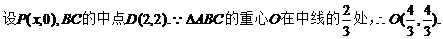
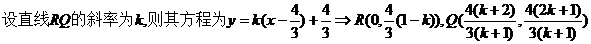 。
。
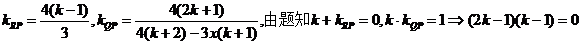
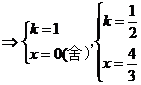
选D
二、填空题:本大题共8小题,考生作答7小题,每小题5分,共35分.
(一)选做题(请考生在第9、10、11三题中任选两题作答,如果全做,则按前两题计分)
9.在平面直角坐标系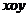 中,若
中,若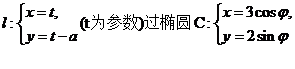
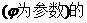 右顶点,则常数
右顶点,则常数 3 .
3 .
【答案】 3
【解析】 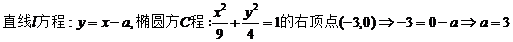
10.已知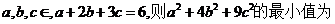 12 .
12 .
【答案】 12
【解析】 
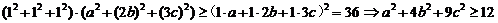
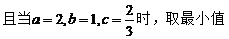 .
.
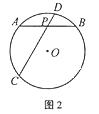
11.如图2,在半径为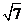 的
的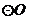 中,弦
中,弦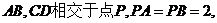
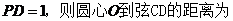 .
.
【答案】 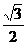
【解析】
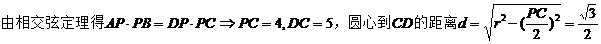
(一) 必做题(12-16题)
12.若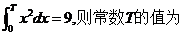 3 .
3 .
【答案】 3
【解析】
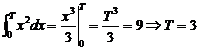
13.执行如图3所示的程序框图,如果输入 9 .
9 .
【答案】 9
【解析】 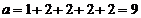
14.设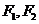 是双曲线
是双曲线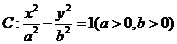 的两个焦点,P是C上一点,若
的两个焦点,P是C上一点,若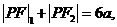 且
且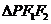 的最小内角为
的最小内角为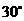 ,则C的离心率为___。
,则C的离心率为___。
【答案】 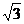
【解析】 设P点在右支上,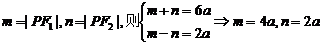
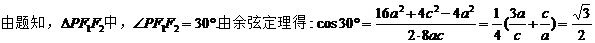
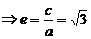
15.设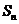 为数列
为数列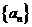 的前n项和,
的前n项和,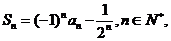 则
则
(1)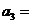 _____;
_____;
(2)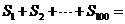 ___________。
___________。
【答案】 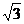
【解析】 设P点在右支上,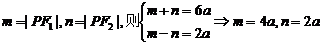
16.设函数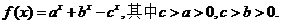
(1)记集合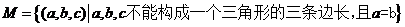 ,则
,则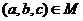 所对应的
所对应的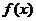 的零点的取值集合为__
的零点的取值集合为__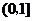 __。
__。
【答案】 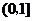
【解析】 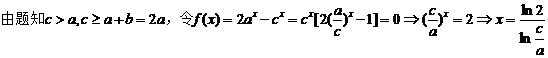
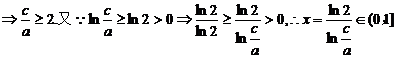 。
。
所以f(x)的零点集合为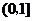
(2)若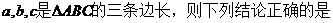 ①②③ .(写出所有正确结论的序号)
①②③ .(写出所有正确结论的序号)
①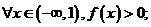
②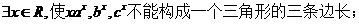
③若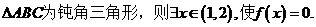
【答案】 ①②③
【解析】 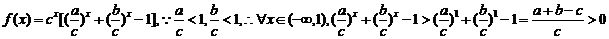 1
1
所以①正确。
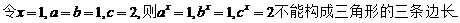 所以②正确。
所以②正确。
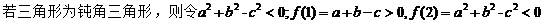
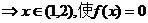 。所以③正确。
。所以③正确。
三、解答题:本大题共6小题,共75分。解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
已知函数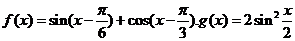 。
。
(I)若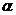 是第一象限角,且
是第一象限角,且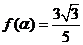 。求
。求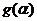 的值;
的值;
(II)求使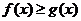 成立的x的取值集合。
成立的x的取值集合。
【答案】 (I)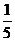 (II)
(II)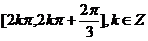
【解析】 (I)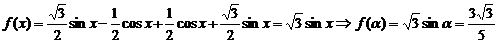 .
.
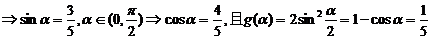
(II)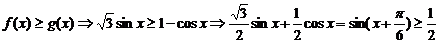
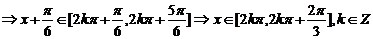 .(完)
.(完)
18.(本小题满分12分)
某人在如图4所示的直角边长为4米的三角形地块的每个格点(指纵、横的交叉点记忆三角形的顶点)处都种了一株相同品种的作物。根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如下表所示:
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
这里,两株作物“相近”是指它们之间的直线距离不超过1米。
(I)从三角形地块的内部和边界上分别随机选取一株作物,求它们恰好“相近”的概率;
(II)从所种作物中随机选取一株,求它的年收获量的分布列与数学期望。
【答案】 (Ⅰ) 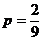 (Ⅱ)
(Ⅱ)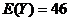
【解析】 (Ⅰ) 由图知,三角形边界共有12个格点,内部共有3个格点.
从三角形上顶点按逆时针方向开始,分别有0,0,1,1,0,1,1,0,0,1,2,1对格点,共8对格点恰好“相近”。
所以,从三角形地块的内部和边界上分别随机选取一株作物,它们恰好“相近”的概率
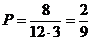
(Ⅱ)三角形共有15个格点。
与周围格点的距离不超过1米的格点数都是1个的格点有2个,坐标分别为(4,0),(0,4)。
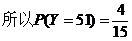
与周围格点的距离不超过1米的格点数都是2个的格点有4个,坐标分别为(0,0), (1,3), (2,2),(3,1)。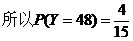
与周围格点的距离不超过1米的格点数都是3个的格点有6个,坐标分别为(1,0), (2,0), (3,0),(0,1,) ,(0,2),(0,3,)。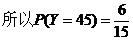
与周围格点的距离不超过1米的格点数都是4个的格点有3个,坐标分别为(1,1), (1,2), (2,1)。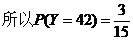
如下表所示:
X | 1 | 2 | 3 | 4 |
Y | 51 | 48 | 45 | 42 |
频数 | 2 | 4 | 6 | 3 |
概率P |
|
|
|
|
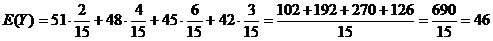
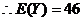 . (完)
. (完)
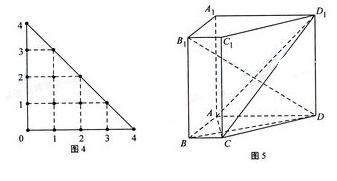
19.(本小题满分12分)如图5,在直棱柱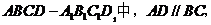
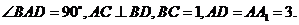
(I)证明: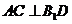 ;
;
(II)求直线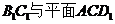 所成角的正弦值。
所成角的正弦值。
【答案】 (Ⅰ) 见下 (Ⅱ)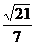
【解析】 (Ⅰ) 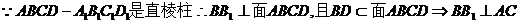
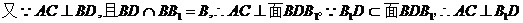 . (证毕)
. (证毕)
(Ⅱ)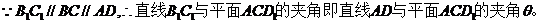
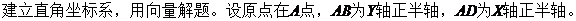
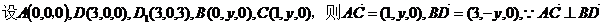


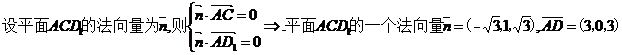
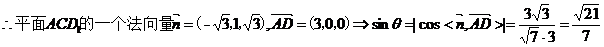
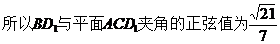 。(完)
。(完)
20.(本小题满分13分)
在平面直角坐标系xOy中,将从点M出发沿纵、横方向到达点N的任一路径成为M到N的一条“L路径”。如图6所示的路径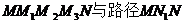 都是M到N的“L路径”。某地有三个新建的居民区,分别位于平面xOy内三点
都是M到N的“L路径”。某地有三个新建的居民区,分别位于平面xOy内三点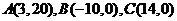 处。现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心。
处。现计划在x轴上方区域(包含x轴)内的某一点P处修建一个文化中心。
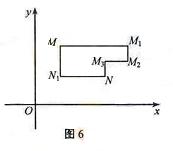
(I)写出点P到居民区A的“L路径”长度最小值的表达式(不要求证明);
(II)若以原点O为圆心,半径为1的圆的内部是保护区,“L路径”不能进入保护区,请确定点P的位置,使其到三个居民区的“L路径”长度值和最小。
【答案】 (Ⅰ)d= |x – 3| + |y – 20|,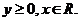
(Ⅱ)当点P(x,y)满足P(3,1)时, 其到三个居民区的“L路径”长度值和最小为45
【解析】 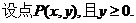
(Ⅰ) 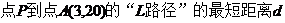 ,
,
 ,其中
,其中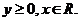
(Ⅱ)本问考查分析解决应用问题的能力,以及绝对值的基本知识。
点P到A,B,C三点的“L路径”长度之和的最小值d = 水平距离之和的最小值h + 垂直距离之和的最小值v。且h和v互不影响。显然当y=1时,v = 20+1=21;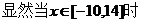 ,水平距离之和h=x – (-10) + 14 – x + |x-3|
,水平距离之和h=x – (-10) + 14 – x + |x-3| 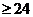 ,且当x=3时,h=24.因此,当P(3,1)时,d=21+24=45.
,且当x=3时,h=24.因此,当P(3,1)时,d=21+24=45.
所以,当点P(x,y)满足P(3,1)时,点P到A,B,C三点的“L路径”长度之和d的最小值为45.
21.(本小题满分13分)
过抛物线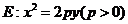 的焦点F作斜率分别为
的焦点F作斜率分别为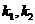 的两条不同的直线
的两条不同的直线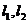 ,且
,且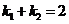 ,
,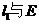 相交于点A,B,
相交于点A,B,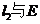 相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为
相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为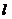 。
。
(I)若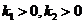 ,证明;
,证明;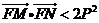 ;
;
(II)若点M到直线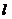 的距离的最小值为
的距离的最小值为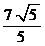 ,求抛物线E的方程。
,求抛物线E的方程。
【答案】 (Ⅰ) 见下 (Ⅱ)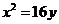
【解析】 (Ⅰ) 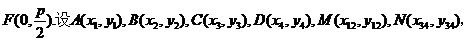

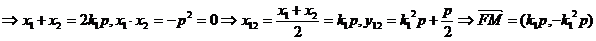
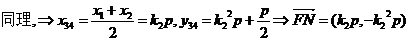 .
.
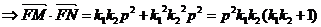
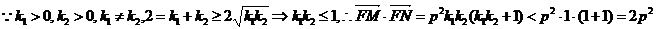 所以,
所以,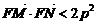 成立. (证毕)
成立. (证毕)
(Ⅱ)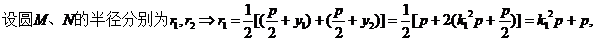
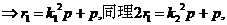
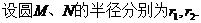 则
则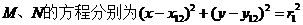 ,
,
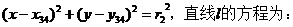
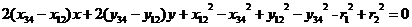 .
.
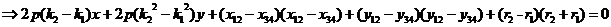
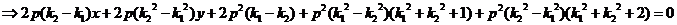
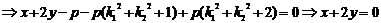
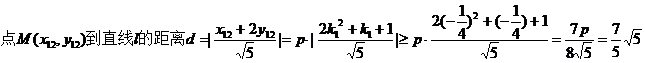
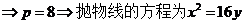 .(完)
.(完)
22.(本小题满分13分)
已知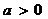 ,函数
,函数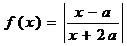 。
。
(I);记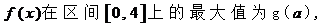 求
求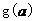 的表达式;
的表达式;
(II)是否存在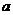 ,使函数
,使函数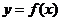 在区间
在区间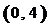 内的图像上存在两点,在该两点处的切线相互垂直?若存在,求
内的图像上存在两点,在该两点处的切线相互垂直?若存在,求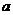 的取值范围;若不存在,请说明理由。
的取值范围;若不存在,请说明理由。
【答案】 (Ⅰ) 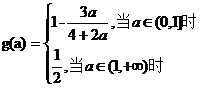 (Ⅱ)
(Ⅱ)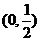
【解析】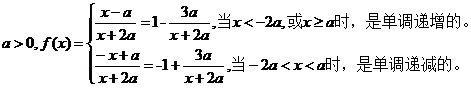
(Ⅰ)

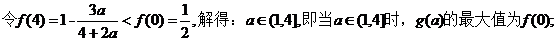
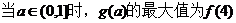
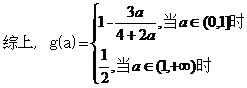
(II)由前知,y=f(x)的图像是由两段反比例函数的图像组成的。因此,若在图像上存在两点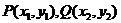 满足题目要求,则P,Q分别在两个图像上,且
满足题目要求,则P,Q分别在两个图像上,且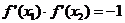 。
。
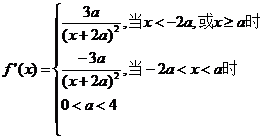
不妨设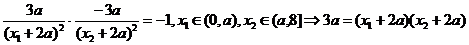
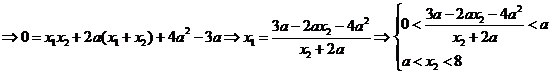
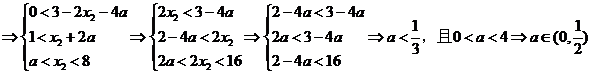
所以,当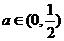 时,函数
时,函数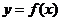 在区间
在区间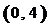 内的图像上存在两点,在该两点处的切线相互垂直.(完)
内的图像上存在两点,在该两点处的切线相互垂直.(完)