一、选择题．每题3分，共5小题，共15分．只有一个正确答案．

1．（3分）四个数﹣1，0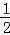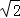，，中为无理数的是（　　）

A． ﹣1 B． 0 C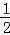． D．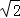

2．（3分）从上面看如图所示的几何体，得到的图形是（　　）

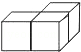
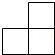A． B． C． D．

3．（3分）数据2，4，3，4，5，3，4的众数是（　　）

A． 5 B． 4 C． 3 D． 2

4．（3分）不等式组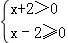的解集是（　　）

A． x≥2 B． x＞﹣2 C． x≤2 D． ﹣2＜x≤2

5．（3分）若一个多边形的内角和小于其外角和，则这个多边形的边数是（　　）

A． 3 B． 4 C． 5 D． 6

二、填空题．每题3分，共8题，共24分．

6．（3分）﹣3的相反数是 　．

7．（3分）若∠α=42°，则∠α的余角的度数是 　．

8．（3分）分解因式：m2﹣2m= 　．

9．（3分）化简：3a2b÷ab= 　．

10．（3分）“节约光荣，浪费可耻”，据统计我国每年浪费粮食约8000000吨，这个数据用科学记数法可表示为 　吨．

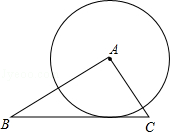
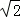11．（3分）如图，在△ABC中，AB=2，AC=，以A为圆心，1为半径的圆与边BC相切，则∠BAC的度数是 　度．

12．（3分）分式方程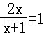的解x= 　．

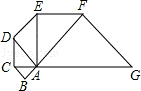
13．（3分）如图，已知△ABC是腰长为1的等腰直角三形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，则第2013个等腰直角三角形的斜边长是 　．

三、解答题．共10小题，共81分．

14．（7分）计算：．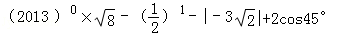

15．（7分）解方程组．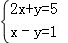

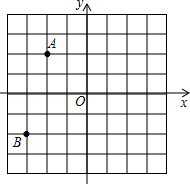
16．（7分）如图，在平面直角坐标系中，A（﹣2，2），B（﹣3，﹣2）

（1）若点C与点A关于原点O对称，则点C的坐标为 　；

（2）将点A向右平移5个单位得到点D，则点D的坐标为 　；

（3）由点A，B，C，D组成的四边形ABCD内（不包括边界）任取一个横、纵坐标均为整数的点，求所取的点横、纵坐标之和恰好为零的概率．

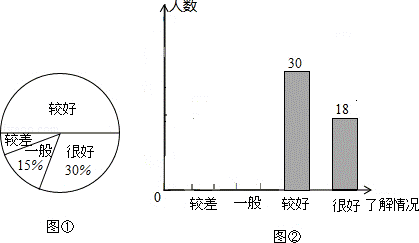
17．（7分）“安全教育，警钟长鸣”，为此，某校随机抽取了九年级（1）班的学生对安全知识的了解情况进行了一次调查统计．图①和图②是通过数据收集后，绘制的两幅不完整的统计图．请你根据图中提供的信息，解答以下问题：

（1）九年级（1）班共有 　名学生；

（2）在扇形统计图中，对安全知识的了解情况为“较差”部分所对应的圆心角的度数是　 　；

（3）若全校有1500名学生，估计对安全知识的了解情况为“较差”、“一般”的学生共有 　名．

18（8分）已知，一次函数y=x+1的图象与反比例函数y=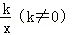的图象都经过点A（a，2）．

（1）求a的值及反比例函数的表达式；

（2）判断点B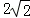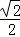（，）是否在该反比例函数的图象上，请说明理由．

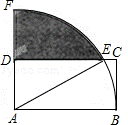
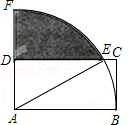
19．（8分）如图，在矩形ABCD中，AB=2DA，以点A为圆心，AB为半径的圆弧交DC于点E，交AD的延长线于点F，设DA=2．

（1）求线段EC的长；

（2）求图中阴影部分的面积．

20．（8分）为建设环境优美、文明和谐的新农村，某村村委会决定在村道两旁种植A，B两种树木，需要购买这两种树苗1000棵．A，B两种树苗的相关信息如表：

设购买A种树苗x棵，绿化村道的总费用为y元，解答下列问题：

（1）写出y（元）与x（棵）之间的函数关系式；

（2）若这批树苗种植后成活了925棵，则绿化村道的总费用需要多少元？

（3）若绿化村道的总费用不超过31000元，则最多可购买B种树苗多少棵？

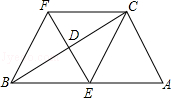
21．（8分）如图，在四边形ABFC中，∠ACB=90°，BC的垂直平分线EF交BC于点D，交AB与点E，且CF=AE，

（1）求证：四边形BECF是菱形；

（2）若四边形BECF为正方形，求∠A的度数．

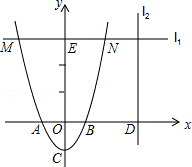
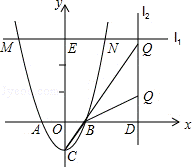
22．（10分）如图，已知抛物线y=2x2﹣2与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．

（1）写出以A，B，C为顶点的三角形面积；

（2）过点E（0，6）且与x轴平行的直线l1与抛物线相交于M、N两点（点M在点N的左侧），以MN为一边，抛物线上的任一点P为另一顶点做平行四边形，当平行四边形的面积为8时，求出点P的坐标；

（3）过点D（m，0）（其中m＞1）且与x轴垂直的直线l2上有一点Q（点Q在第一象限），使得以Q，D，B为顶点的三角形和以B，C，O为顶点的三角形相似，求线段QD的长（用含m的代数式表示）．

23．（11分）用如图①，②所示的两个直角三角形（部分边长及角的度数在图中已标出），完成以下两个探究问题：

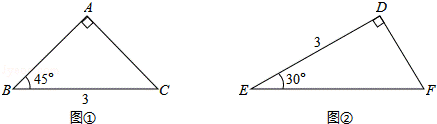
探究一：将以上两个三角形如图③拼接（BC和ED重合），在BC边上有一动点P．

（1）当点P运动到∠CFB的角平分线上时，连接AP，求线段AP的长；

（2）当点P在运动的过程中出现PA=FC时，求∠PAB的度数．

探究二：如图④，将△DEF的顶点D放在△ABC的BC边上的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连接MN．在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由．

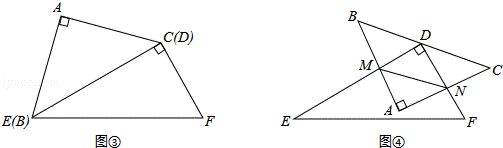
一、选择题．每题3分，共5小题，共15分．只有一个正确答案．

1．D　

2．C　

3．B　

4．A　

5．A　

二、填空题．每题3分，共8题，共24分．

6．　3　．

7．　48°　．

8．　m（m﹣2）　．

9．　3a　．

10．　8×106　．

11．　105　．

12．　1　．

13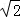．　（）2013　．

三、解答题．共10小题，共81分．

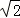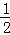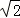14．解：原式=1×2﹣﹣3+2×=﹣．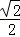　

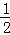15．解：，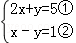

①+②得：3x=6，

解得x=2，

将x=2代入②得：2﹣y=1，

解得：y=1．

∴原方程组的解为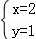

16．解：（1）∵点C与点A（﹣2，2）关于原点O对称，

∴点C的坐标为（2，﹣2）；

（2）∵将点A向右平移5个单位得到点D，

点D的坐标为（3，2）；

（3）由图可知：A（﹣2，2），B（﹣3，﹣2），C（2，﹣2），D（3，2），

∵在平行四边形ABCD内横、纵坐标均为整数的点有15个，其中横、纵坐标和为零的点有3个，即（﹣1，1），（0，0），（1，﹣1），

∴P==．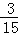

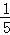故答案为（2，﹣2）；（3，2）；

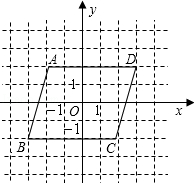
17．解：（1）根据题意得：18÷30%=60（人），

则九年级（1）班的人数为60人；

（2）“一般”的人数为60×15%=9（人），

“较差”的人数为60﹣（9+30+18）=3（人），

则“较差”所占的度数为360°×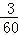=18°；

（3）“较差”、“一般”的学生所占的百分比之和为5%+15%=20%，

则对安全知识的了解情况为“较差”、“一般”的学生共有1500×20%=300（名）．

18．解：（1）将A（a，2）代入y=x+1中得：2=a+1，

解得：a=1，即A（1，2），

将A（1，2）代入反比例解析式中得：k=2，

则反比例解析式为y=；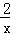

（2）将x=2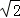代入反比例解析式得：y==，

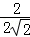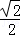则点B在反比例图象上．

19．解；（1）∵在矩形ABCD中，AB=2DA，DA=2，

∴AB=AE=4，

∴DE=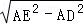=2，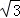

∴EC=CD﹣DE=4﹣2；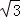

（2）∵sin∠DEA==，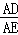

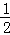∴∠DEA=30°，

∴∠EAB=30°，

∴图中阴影部分的面积为：

S扇形FAB﹣S△DAE﹣S扇形EAB

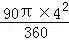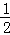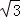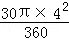
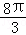=﹣×2×2﹣

=﹣2．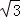

20．解：（1）设购买A种树苗x棵，则购买B种树苗（1000﹣x）棵，由题意，得

y=（20+5）x+（30+5）（1000﹣x）=﹣10x+35000；

（2）由题意，可得0.90x+0.95（1000﹣x）=925，

解得x=500．

当x=500时，y=﹣10×500+35000=30000，

即绿化村道的总费用需要30000元；

（3）由（1）知购买A种树苗x棵，B种树苗（1000﹣x）棵时，总费用y=﹣10x+35000，

由题意，得﹣10x+35000≤31000，

解得x≥400，

所以1000﹣x≤600，

故最多可购买B种树苗600棵．

21．（1）证明：∵EF垂直平分BC，

∴CF=BF，BE=CE，∠BDE=90°，BD=CD，

又∵∠ACB=90°，

∴EF∥AC，

∴BE：AB=DB：BC，

∵D为BC中点，

∴DB：BC=1：2，

∴BE：AB=1：2，

∴E为AB中点，

即BE=AE，

∵CF=AE，

∴CF=BE，

∴CF=FB=BE=CE，

∴四边形BECF是菱形．

（2）解：∵四边形BECF是正方形，

∴∠CBA=45°，

∵∠ACB=90°，

∴∠A=45°．

22．解：（1）∵y=2x2﹣2，

∴当y=0时，2x2﹣2=0，x=±1，

∴点A的坐标为（﹣1，0），点B的坐标为（1，0），AB=2，

又当x=0时，y=﹣2，

∴点C的坐标为（0，﹣2），OC=2，

∴S△ABC=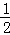AB•OC=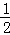×2×2=2；

（2）将y=6代入y=2x2﹣2，

得2x2﹣2=6，x=±2，

∴点M的坐标为（﹣2，6），点N的坐标为（2，6），MN=4．

∵平行四边形的面积为8，

∴MN边上的高为：8÷4=2，

∴P点纵坐标为6±2．

①当P点纵坐标为6+2=8时，2x2﹣2=8，x=±，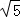

∴点P的坐标为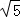（，8），点N的坐标为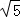（﹣，8）；

②当P点纵坐标为6﹣2=4时，2x2﹣2=4，x=±，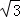

∴点P的坐标为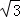（，4），点N的坐标为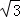（﹣，4）；

（3）∵点B的坐标为（1，0），点C的坐标为（0，﹣2），

∴OB=1，OC=2．

∵∠QDB=∠BOC=90°，

∴以Q，D，B为顶点的三角形和以B，C，O为顶点的三角形相似时，分两种情况：

①OB与BD边是对应边时，△OBC∽△DBQ，

则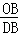=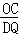，即=，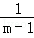

解得DQ=2（m﹣1）=2m﹣2，

②OB与QD边是对应边时，△OBC∽△DQB，

则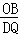=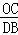，即=，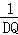

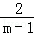解得DQ=．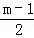

综上所述，线段QD的长为2m﹣2或．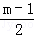

23．解：探究一：（1）依题意画出图形，如答图1所示：

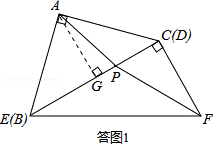
由题意，得∠CFB=60°，FP为角平分线，则∠CFP=30°，

∴CF=BC•sin30°=3×=，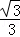

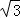∴CP=CF•tan∠CFP=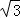×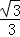=1．

过点A作AG⊥BC于点G，则AG=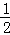BC=，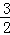

∴PG=CG﹣CP=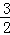﹣1=．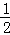

在Rt△APG中，由勾股定理得：

AP===．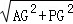

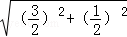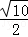（2）由（1）可知，FC=．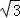

如答图2所示，以点A为圆心，以FC=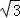长为半径画弧，与BC交于点P1、P2，则AP1=AP2=．

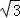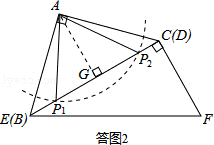
过点A过AG⊥BC于点G，则AG=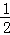BC=．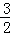

在Rt△AGP1中，cos∠P1AG===，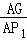

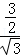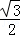∴∠P1AG=30°，

∴∠P1AB=45°﹣30°=15°；

同理求得，∠P2AG=30°，∠P2AB=45°+30°=75°．

∴∠PAB的度数为15°或75°．

探究二：△AMN的周长存在有最小值．

如答图3所示，连接AD．

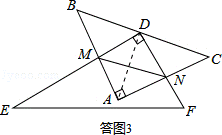
∵△ABC为等腰直角三角形，点D为斜边BC的中点，

∴AD=CD，∠C=∠MAD=45°．

∵∠EDF=90°，∠ADC=90°，

∴∠MDA=∠NDC．

∵在△AMD与△CND中，

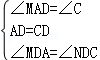
∴△AMD≌△CND（ASA）．

∴AM=CN．

设AM=x，则CN=x，AN=AC﹣CN=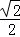BC﹣CN=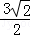﹣x．

在Rt△AMN中，由勾股定理得：

MN====．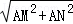

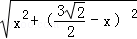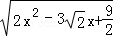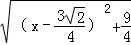△AMN的周长为：AM+AN+MN=+，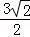

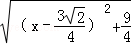当x=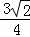时，有最小值，最小值为+=．

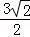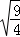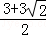∴△AMN周长的最小值为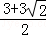．