(单词翻译:单击)
一、选择题(本大题共8小题,每小题4分,共32分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.四个实数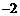 ,
,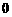 ,
,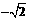 ,
,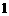 中,最大的实数是
中,最大的实数是
A.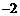 B.
B.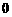 C.
C.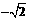 D.
D.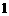
2.下列式子化简后的结果为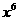 的是
的是
A.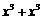 B.
B.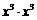 C.
C.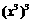 D.
D. 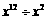
3.小玲在一次班会中参与知识抢答活动,现有语文题6个,数学题5个,综合题9个,她从中随机抽取1个,抽中数学题的概率是
A.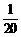 B
B .
.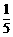 C.
C.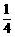 D.
D.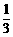
4.下列图形中,既是轴对称图形又是中心对称图形的是

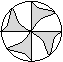


A B C D
5.一 元二次方程
元二次方程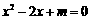 总有实数根,则
总有实数根,则 应满足的条件是
应满足的条件是
A.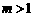 B.
B.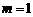 C.
C.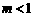 D.
D.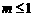
6.正比例函数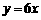 的图象与反比例函数
的图象与反比例函数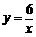 的图象的交点位于
的图象的交点位于
A.第一象限 B.第二象限
B.第二象限
C.第三象限D.第一、三象限
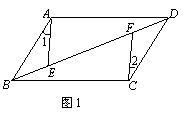
7.如图 ,平行四边形
,平行四边形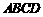 中,
中,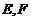 是对角线
是对角线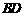 上的两点,如果添加一个条件使
上的两点,如果添加一个条件使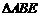 ≌
≌ ,则添加的条件不能是
,则添加的条件不能是
A.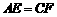 B.
B.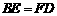 C.
C. 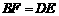 D.
D.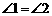
8.如图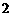 ,在平面直角坐标系
,在平面直角坐标系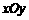 中,半径为
中,半径为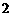 的⊙
的⊙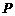 的圆心
的圆心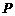 的坐标为
的坐标为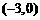 ,将⊙
,将⊙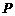 沿
沿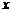 轴正方向平移,使⊙
轴正方向平移,使⊙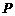 与
与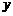 轴相切,则平移的距离为
轴相切,则平移的距离为
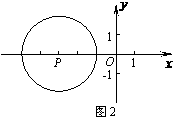
A.1 B.1或5 C.3 D.5
二、填空题(本大题共5小题,每小题4分,共20分.把答案填在答题卡中对应题号后的横线上)
9.若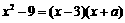 ,则
,则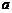
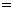 —————— .
—————— .
10.分式方程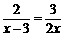 的解为 —————— .
的解为 —————— .
11.小斌所在的课外活动小组在大课间活动中练习立定跳远,成绩如下(单位:米):1.96,2.16,2.04,2.20,1.98,2.22,2.32,则这组数据的中位数是 —————— 米.
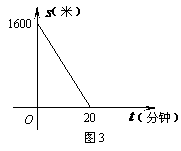
12.小明放学后步行回家,他离家的路程
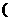 米
米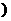 与步行时间
与步行时间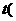 分钟
分钟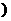 的函数图象如图
的函数图象如图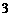 所示,则他步行回家的平均速度是 —————— 米/分钟.
所示,则他步行回家的平均速度是 —————— 米/分钟.
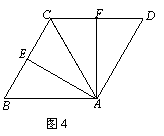
13.如图4,将等边 绕顶点
绕顶点 顺时针方向旋转,使边
顺时针方向旋转,使边 与
与 重合得
重合得 ,
,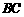 的中点
的中点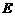 的对应点为
的对应点为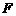 ,则
,则 的度数是_______.
的度数是_______.
三、解答题(本大题共2小题,每小题6分,共12分)
14.计算: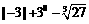 .
.
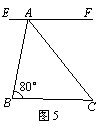
15.如图5,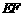 ∥
∥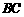 ,
, 平分
平分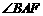 ,
,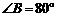 .求
.求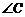 的度数.
的度数.
四、解答题(本大题共3小题,每小题8分,共24分)
16.先化简,再求值: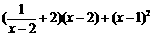 ,其中
,其中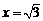 .
.
17.某校为了开阔学生的视野,积极组织学生参加课外读书活动.“放飞梦想”读书小组协助老师随机抽取本校的部分学生,调查他们最喜爱的图书类别(图书分为文学类、艺体类、科普类、其他等四类),并将调查结果绘制成如下两幅不完整的统计图(图6),请你结合图中的信息解答下列问题:
(1)求被调查的学生人数;
(2)补全条形统计图;

(3)已知该校有1200名学生,估计全校最喜爱文学类图书的学生有多少人?
18.“中国 益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端
益阳”网上消息,益阳市为了改善市区交通状况,计划在康富路的北端 修建通往资江北岸的新大桥.如图7,新大桥的两端位于
修建通往资江北岸的新大桥.如图7,新大桥的两端位于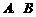 两点,小张为了测量
两点,小张为了测量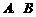 之间的河宽,在垂直于新大桥
之间的河宽,在垂直于新大桥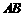 的直线型道路
的直线型道路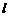 上测得如下数据:
上测得如下数据: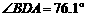 ,
,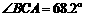 ,
,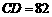 米.求
米.求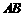 的长(精确到
的长(精确到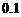 米).
米).

参考数据:

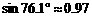 ,
,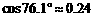 ,
,
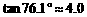 ;
; 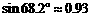 ,
,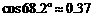 ,
,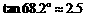 .
.
五、解答题(本大题共2小题,每小题10分,共20分)
19.某电器超市销售每台进价分别为 元、
元、 元的
元的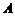 、
、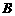 两种型号的电风扇,下表是近两周的销售情况:
两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 |
| ||
第一周 | 3台 | 5台 | 1800元 |
第二周 | 4台 | 10台 | 3100元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求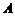 、
、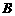 两种型号的电风扇的销售单价;
两种型号的电风扇的销售单价;
(2)若超市准备用不多于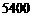 元的金额再采购这两种型号的电风扇共
元的金额再采购这两种型号的电风扇共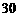 台,求
台,求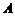 种型号的电风扇最多能采购多少台?
种型号的电风扇最多能采购多少台?
(3)在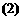 的条件下,超市销售完这
的条件下,超市销售完这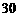 台电风扇能否实现利润为
台电风扇能否实现利润为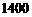 元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
元的目标,若能,请给出相应的采购方案;若不能,请说明理由.
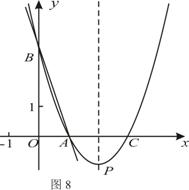
20.如图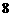 ,直线
,直线
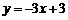 与
与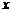 轴、
轴、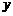 轴分别交于点
轴分别交于点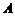 、
、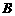 ,抛物线
,抛物线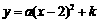 经过点
经过点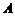 、
、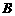 ,并与
,并与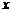 轴交于另一点
轴交于另一点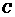 ,其顶点为
,其顶点为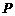 .
.
(1)求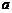 ,
,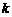 的值;
的值;
(2)抛物线的对称轴上有一点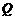 ,使
,使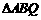 是以
是以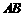 为底边的等腰三角形,求
为底边的等腰三角形,求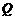 点的坐标.
点的坐标.
(3)在抛物线及其对称轴上分别取点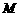 、
、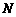 ,使以
,使以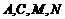 为顶点的四边形为正方形,求此正方形的边长
为顶点的四边形为正方形,求此正方形的边长 .
.
六、解答题(本题满分12分)
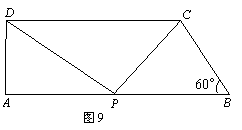
21.如图9,在直角梯形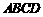 中,
中,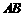 ∥
∥ ,
,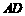 ⊥
⊥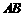 ,
,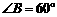 ,
,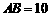 ,
,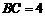 ,点
,点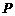 沿线段
沿线段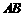 从点
从点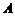 向点
向点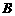 运动,设
运动,设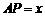 .
.
(1)求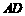 的长;
的长;
(2)点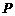 在运动过程中,是否存在以
在运动过程中,是否存在以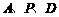 为顶点的三角形与以
为顶点的三角形与以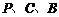 为顶点的三角形相似?若存在,求出
为顶点的三角形相似?若存在,求出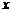 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)设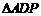 与
与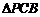 的外接圆的面积分别为
的外接圆的面积分别为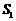 、
、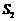 ,若
,若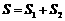 ,求
,求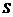 的最小值.
的最小值.
_ueditor_page_break_tag_益阳市2014年普通初中毕业学业考试试卷
数学参考答 案及评分标准
案及评分标准
一、选择题(本大题共8小题,每小题4分,共32分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | D | B | C | C | D | D | A | B |
二、填空题(本大题共5小题,每小题4分,共20分)
9.3; 10.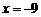 ; 11.2.16; 12.80; 13.
; 11.2.16; 12.80; 13.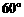 .
.
三、解答题(本大题共2小题,每小题6分,共12分)
14.解:原式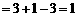 .…………………………………………………………………6分
.…………………………………………………………………6分
15. 解:∵
解:∵ ∥
∥ ,
,
∴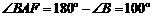 .……………………………………………………2分
.……………………………………………………2分
∵ 平分
平分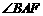 ,
,
∴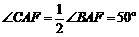 ,………………………………………………………4分
,………………………………………………………4分
∵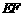 ∥
∥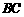 ,
,
∴ .……………………………………………………………6分
.……………………………………………………………6分
四、解答题(本大题共3小题,每小题8分,共24分)
16.解: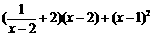
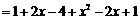
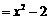 ……………………………………………………………………………6分
……………………………………………………………………………6分
当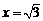 时,原式
时,原式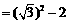
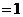 .…………………………………………………8分
.…………………………………………………8分
17.解:(1)被调查的学生人数为: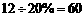
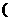 人
人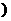 ;……………………………2分
;……………………………2分
(2)如图
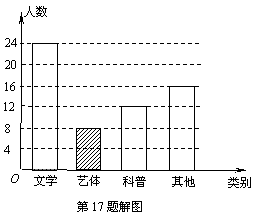 ……………………5分
……………………5分
(3)全校最喜爱文学类图书的学生约有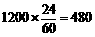
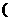 人
人 .………………8分
.………………8分
18.解:设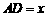 米,则
米,则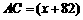 米.
米.
在Rt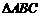 中,
中,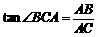 ,∴
,∴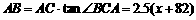 .…………2分
.…………2分
在Rt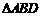 中,
中,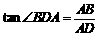 ,∴
,∴ .……………………4分
.……………………4分
∴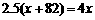 ,∴
,∴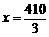 .………………………………………………………6分
.………………………………………………………6分
∴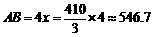 .
.
答: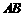 的长约为
的长约为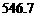 米. …………………………………………………………8分
米. …………………………………………………………8分
五、解答题(本大题共2小题,每小题10分,共20分)
19.解:(1)设 、
、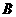 两种型号电风扇的销售单价分别为
两种型号电风扇的销售单价分别为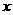 元、
元、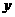 元.依题意得:
元.依题意得:
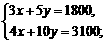 解得
解得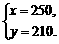
答: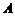 、
、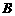 两种型号电风扇的销售单价分别为
两种型号电风扇的销售单价分别为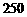 元、
元、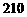 元.……………4分
元.……………4分
(2)设采购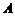 种型号电风扇
种型号电风扇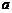 台,则采购
台,则采购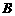 种型号电风扇
种型号电风扇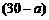 台.
台.
依题意得: ≤
≤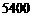 ,
,
解得: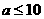 .
.
答:超市最多采购 种型号电风扇
种型号电风扇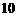 台时,采购金额不多于
台时,采购金额不多于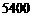 元.………7分
元.………7分
(3)依题意有: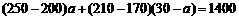 ,
,
解得: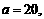 此时,
此时,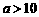 .
.
所以在(2)的条件下超市不能实现利润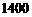 元的目标. …………………10分
元的目标. …………………10分
20. 解:(1)∵直线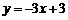 与
与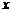 轴、
轴、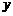 轴分别交于点
轴分别交于点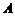 、
、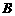 ,
,
∴ ,
,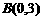 .
.
又抛物线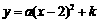 经过点
经过点 ,
,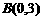 ,
,
∴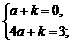 解得
解得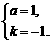
即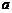 ,
,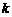 的值分别为
的值分别为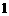 ,
,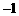 .………………………………………………3分
.………………………………………………3分
(2)设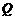 点的坐标为
点的坐标为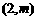 ,对称
,对称 轴
轴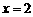 交
交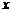 轴于点
轴于点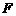 ,
, 过点
过点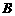 作
作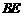 垂直于直线
垂直于直线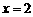 于点
于点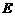 .
.
在Rt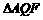 中,
中,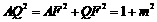 ,
,
在Rt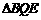 中,
中,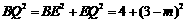 .
.
∵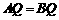 ,∴
,∴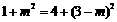 ,∴
,∴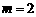 .
.
∴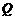 点的坐标为
点的坐标为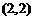 .………………………………………………………6分
.………………………………………………………6分
(3)当点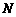 在对称轴上时,
在对称轴上时,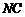 与
与 不垂直.所以
不垂直.所以 应为正方形的对角线.
应为正方形的对角线.
又对称轴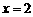 是
是 的中垂线,所以,
的中垂线,所以,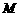 点与顶点
点与顶点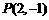 重合,
重合,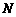 点为点
点为点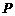 关于
关于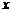 轴的对称点,其坐标为
轴的对称点,其坐标为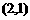 .
.
此时,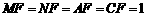 ,且
,且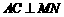 ,
,
∴ 四边形 为正方形.
为正方形.
在Rt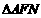 中,
中,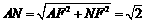 ,即正方形的边长为
,即正方形的边长为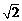 .……10分
.……10分

六、解答题(本题满分12分)
21.解:(1)过点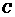 作
作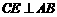 于
于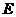 .在Rt
.在Rt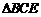 中,
中,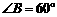 ,
,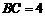 .
.
∴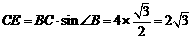 ,
,
∴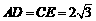 . ………………………………………………………………2分
. ………………………………………………………………2分
(2)存在.若以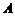 、
、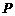 、
、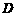 为顶点的三角形与以
为顶点的三角形与以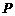 、
、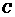 、
、 为顶点的三角形相似,
为顶点的三角形相似,
则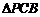 必有一个角是直角. ……………………………………………………3分
必有一个角是直角. ……………………………………………………3分
①当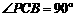 时,在Rt
时,在Rt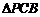 中,
中,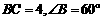 ,
,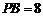 ,
,
∴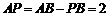 .
.
又由(1)知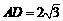 ,在Rt
,在Rt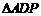 中 ,
中 ,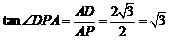 ,
,
∴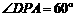 ,∴
,∴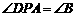 .
.
∴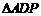 ∽
∽ . ………………………………………………………………5分
. ………………………………………………………………5分
②当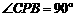 时,在Rt
时,在Rt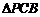 中,
中,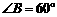 ,
,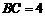 ,
,
∴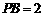 ,
,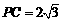 ,∴
,∴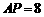 .
.
则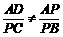 且
且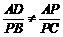 ,此时
,此时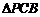 与
与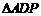 不相似.
不相似.
∴存在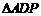 与
与 相似,此时
相似,此时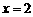 .………………………………………7分
.………………………………………7分
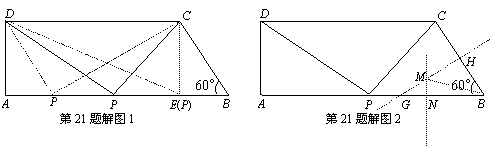
(3)如图,因为Rt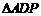 外接圆的直径为斜边
外接圆的直径为斜边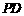 ,
,
∴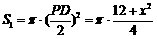 .
.
①当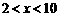 时,作
时,作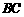 的垂直平分线交
的垂直平分线交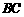 于
于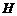 ,交
,交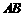 于
于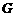 ;作
;作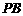 的垂
的垂
直平分线交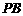 于
于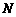 ,交
,交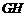 于
于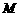 ,连结
,连结 .则
.则 为
为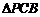 外接圆的半径.
外接圆的半径.
在Rt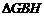 中,
中,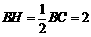 ,
,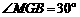 ,∴
,∴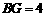 ,
,
又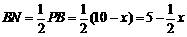 ,∴
,∴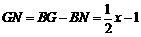 .
.
在Rt 中,∴
中,∴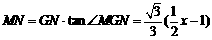 .
.
在Rt 中,
中,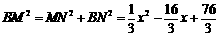 ,
,
∴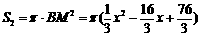 .
.
②当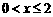 时,
时, 也成立. …………………………10分
也成立. …………………………10分
∴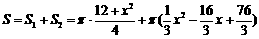
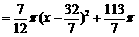 .
.
∴当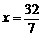 时,
时,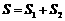 取得最小值
取得最小值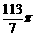 . ………………………………12分
. ………………………………12分

 B种型号
B种型号
