(单词翻译:单击)
一、选择题(本大题共8个小题,每小题有且只有一个正确答案,请将正确答案的选项代号涂在答题卡相应的位置上,每小题3分,满分24分)
1、-5的相反数是
A、5 B、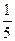 C、-5 D、
C、-5 D、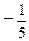
2、一组数据1,2,2,3。下列说法正确的是
A、众数是3 B、中位数是2 C、极差是3 D、平均数是3
3、 右图是由三个小方体叠成的一个立体图形,那么它的俯视图是
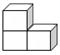

A、 B、 C、 D、
4下列图形中,是中心对称图形的是
A、平行四边形 B、正五边形 C、等腰梯形 D、直角三角形
5、一元二次方程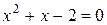 的解为
的解为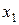 、
、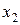 ,则
,则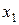 ·
·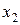 =
=
A、1 B、-1 C、2 D、 -2
6、下列命题正确的是
A、三角形的中位线平行且等于第三边 B、对角线相等的四边形是等腰梯形
C、四条边都相等的四边形是菱形 D、相等的角是对顶角
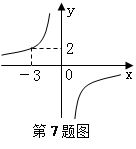
7、如下图,点P(-3,2)是反比例函数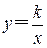 (
(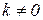 )的图象上一点,则反比例函数的解析式为
)的图象上一点,则反比例函数的解析式为
A、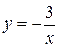 B、
B、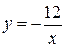 C、
C、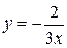 D、
D、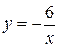
8、如下图,在△ABC中,AB=AC,点D、E在BC上,连续AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为
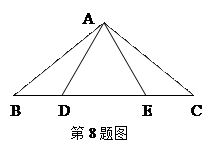
A、BD=CE B、AD=AE C、DA=DE D、BE=CD
二、填空题(本大题共8个小题,请将答案写在答题卡的相应位置上,每小题3分,满分24分)
9、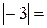 。
。
10、如右图,已知:AB∥CD,∠C=25°,∠E=30°,则∠A= 。
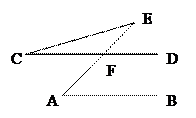
11、到2012年底,湘潭地区总人口约为3020000人,用科学记数法表示这一数为 。
12、湖园中学学生志愿服务小组在“三月学雷锋”活动中,购买了一批牛奶到敬老院慰问老人,如果送给每位老人2盒牛奶,那么剩下16盒;如果送给每位老人3盒牛奶,则正好送完,设敬老院有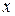 位老人,依题意可列方程为 。
位老人,依题意可列方程为 。
13、“五一”假期,科科随父母在韶山旅游时购买了10张韶山风景明信片(除图案外,形状大小、质地等都相同),其中4张印有主席故居图案,3张印有主席铜像图案,3张印有滴水洞风景图案,他从中任意抽取1张寄给外地工作的姑姑,则恰好抽中印有主席故居图案明信片的概率是 。
14、函数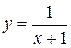 中,自变量
中,自变量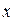 的取值范围为 。
的取值范围为 。
15、计算: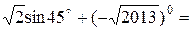 。
。
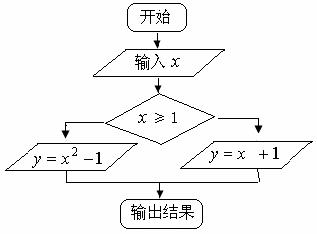
16、如下图,根据所示程序计算,若输入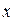 =
=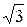 , 则输出结果为 。
, 则输出结果为 。
三、解答题(本大题共10个小题,解答应写出文字说明、证明过程或演算步骤,请将解答过程写在答题卡相应的位置上,满分72分)
17、(本题6分)解不等式组
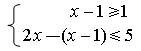
18、(本题6分)
先化简,再求值: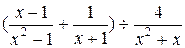 ,其中
,其中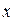 =-2
=-2
19、(本题6分)如图,C岛位于我南海A港口北偏东60方向,距A港口60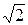 海里处,我海监船从A港口出发,自西向东航行至B处时,接上级命令赶赴C岛执行任务,此时C岛在B处北偏西45°方向上,海监船立刻改变航向以每小时60海里的速度沿BC行进,则从B处到达C岛需要多少小时?
海里处,我海监船从A港口出发,自西向东航行至B处时,接上级命令赶赴C岛执行任务,此时C岛在B处北偏西45°方向上,海监船立刻改变航向以每小时60海里的速度沿BC行进,则从B处到达C岛需要多少小时?

20、(本题6分)2013年4月20日8时,四川省芦山县发生7.0级地震,某市派出抢险救灾工程队赶芦山支援,工程队承担了2400米道路抢修任务,为了让救灾人员和物资尽快运抵灾区,实际施工速度比原计划每小时多修40米,结果提前2小时完成,求原计划每小时抢修道路多少米?
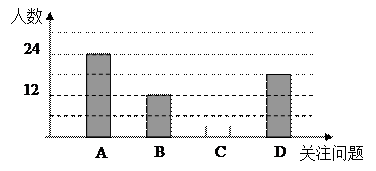
21、(本题6分)6月5日是世界环境日,今年“世界环境日”中国的主题为“同呼吸,共奋斗”,旨在释放和传递:建设美丽中国,人人共享、人人有责的信息,小文积极学习与宣传,并从四个方面A:空气污染,B:淡水资源危机,C:土地荒漠化,D:全球变暖,对全校同学进行了随机抽样调查,了解他们在这四个方面中最关注的问题(每人限选一项)。图1和图2是他收集数据后,绘制的不完整的统计图表,请你根据图表中提供的信息解答以下问题:
关注问题 | 频数 | 频率 |
A | 24 | 0.4 |
B | 12 | 0.2 |
C | n | 0.1 |
D | 18 | m |
合计 | a |
|
(1)根据图表信息,可得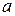 = ;(2分)
= ;(2分)
(2)请你将图2补充完整;(2分)
(3)如果小文所在的学校有1200名学生,那么你根据小文提供的信息估计该校关注“全球变暖”的学生大约有多少人?(2分)
22、(本题6分)莲城超市以10元/件的价格调进一批商品,根据前期销售情况,每天销售量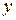 (件)与该商品定价
(件)与该商品定价 (元)是一次函数关系,如图所示。
(元)是一次函数关系,如图所示。
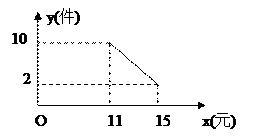
(1)求销售量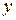 与定价
与定价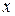 之间的函数关系式;(4分)
之间的函数关系式;(4分)
(2)如果超市将该商品的销售价定为13元/件,不考虑其它因素,求超市每天销售这种商品所获得的利润。(2分)
23、(本题8分)5月12日是母亲节,小明去花店买花送给母亲,挑中了象征温馨、母爱的康乃馨和象征高贵、尊敬的兰花两种花,已知康乃馨每支5元,兰花每支3元,小明只有30元,希望购买花的支数不少于7支,其中至少有一支是康乃馨。
(1)小明一共有多少种可能的购买方案?列出所有方案;(4分)
(2)如果小明先购买一张2元的祝福卡,再从(1)中任选一种方案购花,求他能实现购买愿望的概率。(4分)
24、(本题8分)在数学活动课中,小辉将边长为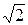 和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF。
和3的两个正方形放置在直线l上,如图1,他连结AD、CF,经测量发现AD=CF。
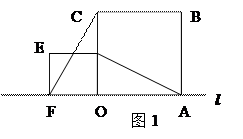
(1)他将正方形ODEF绕O点逆时针旋转一定的角度,如图2,试判断AD与CF还相等吗?说明你的理由;(4分)
(2)他将正方形ODEF绕O点逆时针旋转,使点E旋转至直线l上,如图3,请你求出CF的长。(4分)
25、(本题10分)如图,在坐标系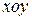 中,已知D(-5,4),B(-3,0),过D点分别作DA、DC垂直于
中,已知D(-5,4),B(-3,0),过D点分别作DA、DC垂直于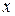 轴,
轴,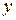 轴,垂足分别为A、C两点,动点P从O点出发,沿
轴,垂足分别为A、C两点,动点P从O点出发,沿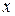 轴以每秒1个单位长度的速度向右运动,运动时间为t秒。
轴以每秒1个单位长度的速度向右运动,运动时间为t秒。
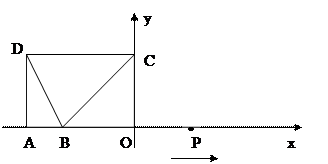
(1)当t为何值时,PC∥DB;(3分)
(2)当t为何值时,PC⊥BC;(4分)
(3)以点P为圆心,PO的长为半径的⊙P随点P的运动而变化,当⊙P与△BCD的边(或边所在的直线)相切时,求t的值。(3分)
26、(本题10分)如图,在坐标系 中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线
中,△ABC是等腰直角三角形,∠BAC=90°,A(1,0),B(0,2),抛物线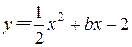 的图象过C点。
的图象过C点。
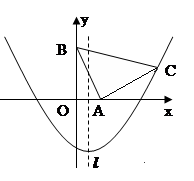
(1)求抛物线的解析式;(3分)
(2)平移该抛物线的对称轴所在直线l。当l移动到何处时,恰好将△ABC的面积分为相等的两部分?(3分)
(3)点P是抛物线上一动点,是否存在点P,使四边形PACB为平行四边形?若存在,求出P点坐标,若不存在,说明理由。(4分)

 1
1
