一、选择题（本大题有7小题，每小题3分，共21分.每小题都有四个选项，其中有且只有一个选项正确）

1．下列计算正确的是

A．－1＋2＝1． B．－1－1＝0． C．(－1)2＝－1． D．－12＝1．

2．已知∠A＝60°，则∠A的补角是

A．160°．B．120°．

C．60°． D．30°．

3．图1是下列一个立体图形的三视图，则这个立体图形是

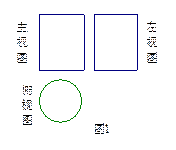
A．圆锥． B．球．

C．圆柱． D．正方体．

4．掷一个质地均匀的正方体骰子，当骰子停止后，朝上一面的点数为5的概率是

A．1． B．． C．． D．0．

5．如图2，在⊙O中，︵AB＝︵AC，∠A＝30°，则∠B＝

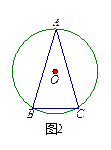
A．150°．B．75°．

C．60°． D．15°．

6．方程＝的解是

A．3． B．2．

C．1． D．0．

7．在平面直角坐标系中，将线段OA向左平移2个单位，平移后，点O，A的对应点分别为点O1，A1.若点O（0，0），A（1，4），则点O1，A1的坐标分别是

A．（0，0），（1，4）． B．（0，0），（3，4）．

C．（－2，0），（1，4）．D．（－2，0），（－1，4）．

二、填空题（本大题有10小题，每小题4分，共40分）

8．－6的相反数是 ．

9．计算：m2·m3＝ ．

10．式子在实数范围内有意义，则实数x的取值范围是 ．

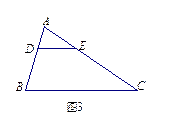
11．如图3，在△ABC中，DE∥BC，AD＝1，AB＝3，DE＝2，则BC＝ ．

12．在一次中学生田径运动会上，参加男子跳高的15名运动员的成绩如下表所示：

则这些运动员成绩的中位数是 米．

13．x2－4x＋4= ()2．

14．已知反比例函数y＝的图象的一支位于第一象限，则常数m的取值范围是 ．

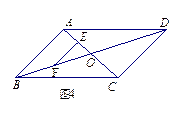
15．如图4，□ABCD的对角线AC，BD相交于点O，点E，F分别是线段AO，BO的中点．若AC＋BD＝24厘米，

△OAB的周长是18厘米，则EF＝ 厘米．

16．某采石场爆破时，点燃导火线的甲工人要在爆破前转移到400米以外的安全区域．甲工人在转移过程中，前40米只能步行，之后骑自行车．已知导火线燃烧的速度为0.01米/秒，步行的速度为1米/秒，骑车的速度为4米/秒．为了确保甲工人的安全，则导火线的长要大于 米．

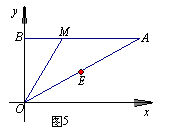
17．如图5，在平面直角坐标系中，点O是原点，点B（0，），点A在第一象限且AB⊥BO，点E是线段AO的中点，点M在线段AB上．若点B和点E关于直线OM对称，且则点M的坐标是 ( ， ) ．

三、解答题（本大题有9小题，共89分）

18．（本题满分21分）

（1）计算：5a＋2b＋(3a—2b)；

（2）在平面直角坐标系中，已知点A（－4,1），B（－2,0），C（－3, －1）,请在图6上画出△ABC，并画出与△ABC关于原点O对称的图形；

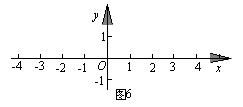
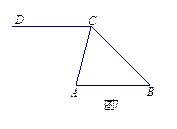
（3）如图7，已知∠ACD＝70°，∠ACB＝60°，∠ABC＝50°.求证：AB∥CD.

19．（本题满分21分）

（1）甲市共有三个郊县，各郊县的人数及人均耕地面积如下表所示：

求甲市郊县所有人口的人均耕地面积（精确到0.01公顷）；

（2）先化简下式，再求值： － ，其中x＝＋1， y＝2—2；

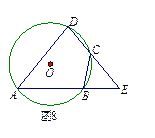
（3）如图8，已知A，B，C，D 是⊙O上的四点，延长DC，AB相交于点E．若BC＝BE．求证：△ADE是等腰三角形.

20．（本题满分6分）有一个质地均匀的正12面体，12个面上分别写有1~12这12个整数（每个面上只有一个整数且每个面上的整数互不相同）.投掷这个正12面体一次，记事件A为 “向上一面的数字是2或3的整数倍”，记事件B为 “向上一面的数字是3的整数倍”，请你判断等式“P(A)＝＋P(B)”是否成立，并说明理由.

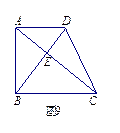
21.（本题满分6分）如图9，在梯形ABCD中，AD∥BC，对角线AC，BD相交于点E，若AE＝4，CE＝8，DE＝3，

梯形ABCD的高是，面积是54.求证：AC⊥BD.

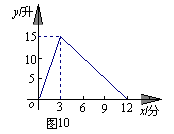
22．（本题满分6分）一个有进水管与出水管的容器，从某时刻开始的3分内只进水不出水，在随后的

9分内既进水又出水，每分的进水量和出水量都是常数.容器内的水量y（单位：升）与时间x（单位：分）之间的关系如图10所示.当容器内的水量大于5升时，求时间x的取值范围.

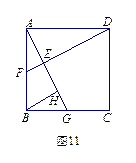
23．（本题满分6分）如图11，在正方形ABCD中，点G是边BC上的任意一点，DE⊥AG，垂足为E，延长DE交AB于

点F.在线段AG上取点H，使得AG＝DE＋HG，连接BH.求证：∠ABH＝∠CDE.

24．（本题满分6分）已知点O是坐标系的原点，直线y＝－x＋m＋n与双曲线y＝交于两个不同的点A（m，n）(m≥2)和B（p，q）,直线y＝－x＋m＋n与y轴交于点C ，求△OBC的面积S的取值范围．

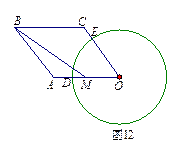
25．（本题满分6分）如图12，已知四边形OABC是菱形，∠O＝60°，点M是OA的中点.以点O为圆心，

r为半径作⊙O分别交OA，OC于点D，E，连接BM.若BM＝， ︵DE的长是．求证：直线BC与⊙O相切.

26．（本题满分11分）若x1，x2是关于x的方程x2＋bx＋c＝0的两个实数根，且＋＝2（k是整数），则称方程x2＋bx＋c＝0为“偶系二次方程”.如方程x2－6x－27＝0，x2－2x－8＝0，x2＋3x－＝0，x2＋6x－27＝0， x2＋4x＋4＝0都是“偶系二次方程”.

（1）判断方程x2＋x－12＝0是否是“偶系二次方程”，并说明理由；

（2）对于任意一个整数b，是否存在实数c，使得关于x的方程x2＋bx＋c＝0是“偶系二次方程”，并说明理由.

2013年厦门市初中毕业及高中阶段各类学校招生考试

数学参考答案及评分标准

一、选择题（本大题共7小题，每小题3分，共21分）

二、填空题（本大题共10小题，每题4分，共40分）

8. 6 9. m5 10.x≥3 11. 6

12. 1.65 13. x—2 14. m＞1

15. 3 16. 1.3 17.（1，）

三、解答题（本大题共9小题，共89分）

18．（本题满分21分）

（1）解：5a＋2b＋(3a—2b)

＝5a＋2b＋3a—2b ……………………………3分

＝8a. ……………………………7分

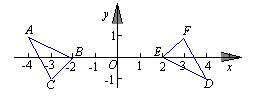
（2）

解： 正确画出△ABC ……………………………10分

正确画出△DEF……………………………14分

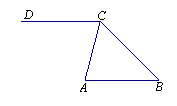
（3）证明1：∵∠ACD＝70°，∠ACB＝60°，

∴∠BCD＝130°. …………16分

∵∠ABC＝50°，

∴∠BCD＋∠ABC＝180°. …………18分

∴AB∥CD. …………21分

证明2：∵∠ABC＝50°，∠ACB＝60°，

∴∠CAB＝180°—50°—60°

＝70°.………………16分

∵∠ACD＝70°，

∴∠CAB＝∠ACD. ………………18分

∴AB∥CD. ………………21分

19．（本题满分21分）

（1）解： ……………………………5分

≈0.17（公顷/人）. ……………………………6分

∴ 这个市郊县的人均耕地面积约为0.17公顷.……………………7分

（2）解： —

＝……………………………9分

＝x－y. ……………………………11分

当 x＝＋1， y＝2—2时，

原式＝ ＋1－(2—2) ……………………………12分

＝3—.……………………………14分

（3）证明： ∵BC＝BE，

∴∠E＝∠BCE. ……………………………15分

∵ 四边形ABCD是圆内接四边形，

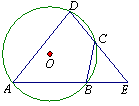
∴∠A＋∠DCB＝180°.……………17分

∵∠BCE＋∠DCB＝180°,

∴∠A＝∠BCE. ………………18分

∴∠A＝∠E. ………………19分

∴ AD＝DE.………………20分

∴△ADE是等腰三角形. ………………21分

20．（本题满分6分）

解：不成立 ……………………………1分

∵ P(A)＝＝，……………………………3分

又∵P(B) ＝＝，……………………………5分

而＋＝≠.

∴ 等式不成立. ……………………………6分

21．（本题满分6分）

证明1：∵AD∥BC，

∴∠ADE＝∠EBC，∠DAE＝∠ECB.

∴△EDA∽△EBC. ……………………………1分

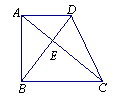
∴ ＝＝. ……………………………2分

即：BC＝2AD. ………………3分

∴54＝×( AD＋2AD)

∴AD＝5. ………………4分

在△EDA中，

∵DE＝3，AE＝4，

∴DE2＋AE2＝AD2. ……………………………5分

∴∠AED＝90°.

∴ AC⊥BD. ……………………………6分

证明2： ∵AD∥BC，

∴∠ADE＝∠EBC，∠DAE＝∠ECB.

∴△EDA∽△EBC. ……………………………1分

∴＝. ……………………………2分

即＝.

∴BE＝6.……………………………3分

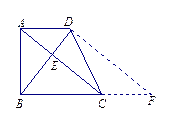
过点D作DF∥AC交BC的延长线于点F.

由于AD∥BC，

∴四边形ACFD是平行四边形.

∴DF＝AC＝12，AD＝CF.

∴BF＝BC＋AD.

∴54＝××BF.

∴BF＝15. ……………………………4分

在△DBF中，

∵DB＝9，DF＝12，BF＝15，

∴DB2＋DF2＝BF2. ……………………………5分

∴∠BDF＝90°.

∴DF⊥BD.

∴AC⊥BD. ……………………………6分

22．（本题满分6分）

解1： 当0≤x≤3时，y＝5x. ……………………………1分

当y＞5时，5x＞5，……………………………2分

解得 x＞1.

∴1＜x≤3. ……………………………3分

当3＜x≤12时，

设 y＝kx＋b.

则解得

∴ y＝－x＋20.……………………………4分

当y＞5时，－x＋20＞5，……………………………5分

解得 x＜9.

∴ 3＜x＜9.……………………………6分

∴容器内的水量大于5升时，1＜x＜9 .

解2： 当0≤x≤3时，y＝5x. ……………………………1分

当y＝5时，有5＝5x，解得 x＝1.

∵ y随x的增大而增大，

∴当y＞5时，有x＞1.……………………………2分

∴ 1＜x≤3. ……………………………3分

当3＜x≤12时，

设 y＝kx＋b.

则解得

∴ y＝－x＋20. ……………………………4分

当y＝5时，5＝－x＋20.

解得x＝9.

∵ y随x的增大而减小，

∴当y＞5时，有x＜9. ……………………………5分

∴3＜x＜9. ……………………………6分

∴容器内的水量大于5升时，1＜x＜9 .

23．（本题满分6分）

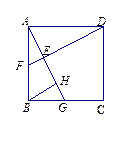
证明1：∵四边形ABCD是正方形，∴∠FAD＝＝90°.

∵DE⊥AG，∴∠AED＝90°.

∴∠FAG＋∠EAD＝∠ADF＋∠EAD

∴∠FAG＝∠ADF.…………………1分

∵AG＝DE＋HG，AG＝AH＋HG，

∴ DE＝AH. ……………………………2分

又AD＝AB，

∴ △ADE≌△ABH.……………………………3分

∴ ∠AHB＝∠AED＝90°.

∵∠ADC＝＝90°，……………………………4分

∴ ∠BAH＋∠ABH＝∠ADF＋∠CDE. ……………………………5分

∴ ∠ABH＝∠CDE.……………………………6分

24．（本题满分6分）

解：∵ 直线y＝－x＋m＋n与y轴交于点C，

∴ C（0，m＋n）.

∵点B（p，q）在直线y＝－x＋m＋n上， ……………………………1分

∴q＝－p＋m＋n. ……………………………2分

又∵点A、B在双曲线y＝上，

∴＝－p＋m＋.

即p－m＝，

∵点A、B是不同的点.

∴ p－m≠0.∴ pm＝1. ……………………………3分

∵ nm＝1，

∴ p＝n，q＝m. ……………………………4分

∵1＞0，∴在每一个象限内，

反比例函数y＝的函数值y随自变量x的增大而减小.

∴当m≥2时，0＜n≤.……………………………5分

∵S＝( p＋q) p

＝p2＋pq

＝n2＋

又∵＞0，对称轴n＝0，

∴当0＜n≤时，S随自变量n的增大而增大.

＜S≤. ……………………………6分

25．（本题满分6分）

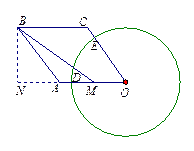
证明一：∵︵DE的长是，∴·60＝.∴ r＝. ……………………1分

作BN⊥OA，垂足为N.

∵四边形OABC是菱形，

∴AB∥CO.

∵∠O＝60°，

∴∠BAN＝60°，∴∠ABN＝30°.

设NA＝x，则AB＝2x，∴ BN＝x. ……………………………2分

∵M是OA的中点，且AB＝OA，

∴ AM＝x. ……………………………3分

在Rt△BNM中，

(x)2＋(2x)2＝()2，

∴ x＝1，∴BN＝. ……………………………4分

∵ BC∥AO，

∴ 点O到直线BC的距离d＝. ……………………………5分

∴ d＝r.

∴ 直线BC与⊙O相切.……………………………6分

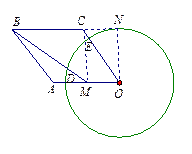
证明二：∵︵DE的长是，∴·60＝.∴ r＝. ……………………1分

延长BC，作ON⊥BC，垂足为N.

∵ 四边形OABC是菱形

∴ BC∥AO，

∴ ON⊥OA.

∵∠AOC＝60°，

∴∠NOC＝30°.

设NC＝x，则OC＝2x， ∴ON＝x ……………………………2分

连接CM， ∵点M是OA的中点，OA＝OC，

∴ OM＝x.……………………………3分

∴四边形MONC是平行四边形.

∵ ON⊥BC，

∴四边形MONC是矩形. ……………………………4分

∴CM⊥BC. ∴ CM＝ON＝x.

在Rt△BCM中，

(x)2＋(2x)2＝()2，

解得x＝1.

∴ON＝CM＝. ……………………………5分

∴ 直线BC与⊙O相切.……………………………6分

26．（本题满分11分）

（1）解：不是……………………………1分

解方程x2＋x－12＝0得，x1＝－4，x2＝3. ……………………………2分

＋＝4＋3＝2×. ……………………………3分

∵3.5不是整数，

∴方程x2＋x－12＝0不是“偶系二次方程”.…………………………4分

（2）解：存在 …………………………6分

∵方程x2－6x－27＝0，x2＋6x－27＝0是“偶系二次方程”，

∴ 假设 c＝mb2＋n.…………………………8分

当 b＝－6，c＝－27时，有 －27＝36m＋n.

∵x2＝0是“偶系二次方程”，

∴n＝0，m＝－ . …………………………9分

即有c＝－ b2.

又∵x2＋3x－＝0也是“偶系二次方程”，

当b＝3时，c＝－ ×32＝－.

∴可设c＝－ b2.…………………………10分

对任意一个整数b，当c＝－ b2时，

∵△＝b2－4c

＝4b2.

∴ x＝ .

∴ x1＝－b，x2＝b.

∴ ＋＝＋＝2.

∵b是整数，∴对任意一个整数b，当c＝－ b2时，关于x的方程x2＋bx＋c＝0是“偶系二次方程”. …………………………11分