(单词翻译:单击)
一、选择题:(本题有10个小题,每小题3分,共30分)
下面每小题给出的四个选项中,只有一个是正确的,请把正确选项的字母填涂在答题卡中相应的格子内.
1.3的倒数是( )
A. 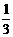 B.
B.  C. -3 D. 3
C. -3 D. 3
2.如图,直线m∥n,则∠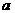 为( )
为( )
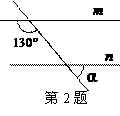
A.70° B. 65° C. 50° D. 40°
3.在下面的四个几何体中,左视图与主视图不相同的几何体是( )
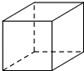
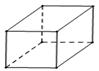
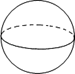
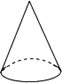
A.正方体 B.长方体 C.球 D.圆锥
4.下列计算正确的是( )
A.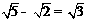 B.
B.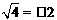 C.
C.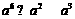 D.
D.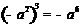
5.为了调查某小区居民的用水情况,随机抽查了若干户家庭的月用水量,结果如下表:
月用水量(吨) | 3 | 4 | 5 | 8 |
户 数 | 2 | 3 | 4 | 1 |
则关于这若干户家庭的月用水量,下列说法错误的是( )
A.众数是4 B.平均数是4.6
C.调查了10户家庭的月用水量 D.中位数是4.5
6.如图,在平行四边形ABCD中,AB=4,BC=6,AC的垂直平分线交AD于点E,则△CDE的周长是( )
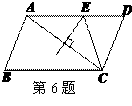
A.7 B.10 C.11 D.12
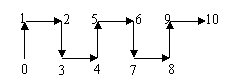
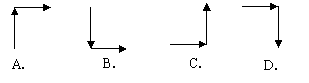
7.根据左图中箭头的指向规律,从2013到2014再到2015,箭头的方向是以下图示中的( )
8.已知: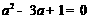 ,则
,则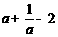 的值为( )
的值为( )
A.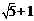 B.1 C.-1 D.-5
B.1 C.-1 D.-5
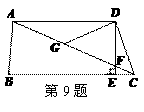
9.如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若DG=3,EC=1,则DE的长为( )
A.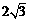 B.
B.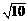 C.
C.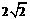 D.
D.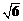
10.已知抛物线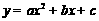 (a≠0)经过点(1,1)和(-1,0).下列结论:①
(a≠0)经过点(1,1)和(-1,0).下列结论:①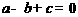 ;②
;②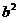 >
>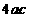 ;③当
;③当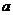 <0时,抛物线与
<0时,抛物线与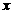 轴必有一个交点在点(1,0)的右侧;④抛物线的对称轴为
轴必有一个交点在点(1,0)的右侧;④抛物线的对称轴为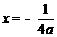 .其中结论正确的个数有( )
.其中结论正确的个数有( )
A.4个 B. 3个 C.2个 D.1个
二、填空题:(本题有6个小题,每小题3分,共18分)
11.世界文化遗产长城总长约6700000 ,用科学记数法表示这个数为_____________
,用科学记数法表示这个数为_____________ .
.
12.计算: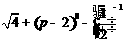 =_____________.
=_____________.
13.不等式组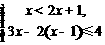 的解集为_____________.
的解集为_____________.
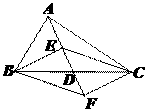
14.如图,在△ABC中,点D是BC的中点,点E,F分别在线段AD及其延长线上,且DE=DF.给出下列条件:①BE⊥EC;②BF∥CE;③AB=AC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是_____________(只填写序号).
15.如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是_____________海里.(结果精确到个位,参考数据: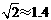 ,
,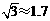 ,
,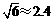 )
)
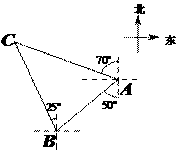
第14题 第15题 第16题
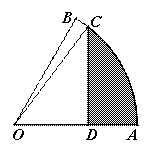
16.如图,扇形OAB中,∠AOB=60°,扇形半径为4,点C在 上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为__________.
上,CD⊥OA,垂足为点D,当△OCD的面积最大时,图中阴影部分的面积为__________.
三、解答题:(本题有9个小题,共72分)
17.(6分)化简: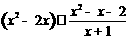 .
.
18.(6分)如图,D在AB上,E在AC上,AB=AC,AD=AE.求证:∠B=∠C.
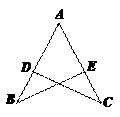
19.(6分)甲、乙两人准备整理一批新到的图书,甲单独整理需要40分钟完工;若甲、乙共同整理20分钟后,乙需再单独整理30分钟才能完工.问乙单独整理这批图书需要多少分钟完工?
20.(9分)据报道,“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目,某校学生会想知道学生对这个提议的了解程度,随机抽取部分学生进行了一次问卷调查,并根据收集到的信息进行了统计,绘制了下面两幅尚不完整的统计图.请你根据统计图中所提供的信息解答下列问题:
条形统计图 扇形统计图
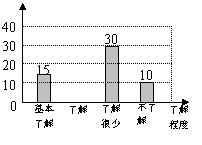
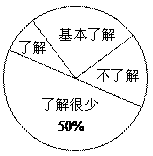
(1)接受问卷调查的学生共有________名,扇形统计图中“基本了解”部分所对应扇形的圆心角为___________;请补全条形统计图;
(2)若该校共有学生900人,请根据上述调查结果,估计该校学生中对将“剪刀石头布”作为奥运会比赛项目的提议达到“了解”和“基本了解”程度的总人数;
(3)“剪刀石头布”比赛时双方每次任意出“剪刀”、“石头”、“布”这三种手势中的一种,规则为:剪刀胜布,布胜石头,石头胜剪刀,若双方出现相同手势,则算打平.若小刚和小明两人只比赛一局,请用树状图或列表法求两人打平的概率.
21.(7分)已知关于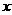 的一元二次方程
的一元二次方程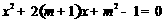 .
.
(1)若方程有实数根,求实数 的取值范围;
的取值范围;
(2)若方程两实数根分别为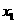 ,
,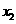 ,且满足
,且满足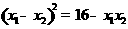 ,求实数
,求实数 的值.
的值.
22.(8分)某市政府为了增强城镇居民抵御大病风险的能力,积极完善城镇居民医疗保险制度,纳入医疗保险的居民的大病住院医疗费用的报销比例标准如下表:
医疗费用范围 | 报销比例标准 |
不超过8000元 | 不予报销 |
超过8000元且不超过30000元的部分 | 50% |
超过30000元且不超过50000元的部分 | 60% |
超过50000元的部分 | 70% |
设享受医保的某居民一年的大病住院医疗费用为x元,按上述标准报销的金额为 y元.
(1)直接写出x≤50000时,y关于x的函数关系式,并注明自变量x的取值范围;
(2)若某居民大病住院医疗费用按标准报销了20000元,问他住院医疗费用是多少元?
23.(8分)如图,点B(3,3)在双曲线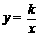 (x>0)上,点D在双曲线
(x>0)上,点D在双曲线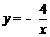 (x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
(x<0)上,点A和点C分别在x轴,y轴的正半轴上,且点A,B,C,D构成的四边形为正方形.
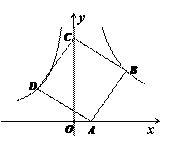
(1)求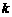 的值;
的值;
(2)求点A的坐标.
24.(10分)如图1,AB为半圆的直径,O为圆心,C为圆弧上一点,AD垂直于过C点的切线,垂足为D,AB的延长线交直线CD于点E.
(1)求证:AC平分∠DAB;
(2)若AB=4,B为OE的中点,CF⊥AB,垂足为点F,求CF的长;
(3)如图2,连接OD交AC于点G,若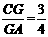 ,求
,求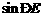 的值.
的值.
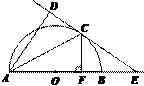
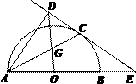
图1 图2
25.(12分)已知抛物线C1: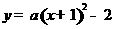 的顶点为A,且经过点B(-2,-1).
的顶点为A,且经过点B(-2,-1).
(1)求A点的坐标和抛物线C1的解析式;
(2)如图1,将抛物线C1向下平移2个单位后得到抛物线C2,且抛物线C2与直线AB相交于C,D两点,求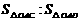 的值;
的值;
(3)如图2,若过P(-4,0),Q(0,2)的直线为l,点E在(2)中抛物线C2对称轴右侧部分(含顶点)运动,直线m过点C和点E.问:是否存在直线m,使直线l,m与x轴围成的三角形和直线l,m与y轴围成的三角形相似?若存在,求出直线m的解析式;若不存在,说明理由.


图1 图2


