一．选择题（共10小题，每小题3分，满分30分）

1．（2013安顺）计算﹣|﹣3|+1结果正确的是（　　）

A．4 B．2 C．﹣2 D．﹣4

考点：有理数的加法；绝对值．

分析：首先应根据负数的绝对值是它的相反数，求得|﹣3|=3，再根据有理数的加法法则进行计算即可．

解答：解：﹣|﹣3|+1=﹣3+1=﹣2．

故选C．

点评：此题考查了有理数的加法，用到的知识点是有理数的加法法则、绝对值，理解绝对值的意义，熟悉有理数的加减法法则是解题的关键．　

2．（2013安顺）某市在一次扶贫助残活动中，共捐款2580000元，将2580000用科学记数法表示为（　　）

A．2.58×107元 B．2.58×106元 C．0.258×107元 D．25.8×106

考点：科学记数法—表示较大的数．

分析：科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．

解答：解：将2580000元用科学记数法表示为：2.58×106元．

故选：B．

点评：此题考查了科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．　

3．（2013安顺）将点A（﹣2，﹣3）向右平移3个单位长度得到点B，则点B所处的象限是（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

考点：坐标与图形变化-平移．

分析：先利用平移中点的变化规律求出点B的坐标，再根据各象限内点的坐标特点即可判断点B所处的象限．

解答：解：点A（﹣2，﹣3）向右平移3个单位长度，得到点B的坐标为为（1，﹣3），

故点在第四象限．

故选D．

点评：本题考查了图形的平移变换及各象限内点的坐标特点．注意平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．　

4．（2013安顺）已知关于x的方程x2﹣kx﹣6=0的一个根为x=3，则实数k的值为（　　）

A．1 B．﹣1 C．2 D．﹣2

考点：一元二次方程的解．

分析：一元二次方程的根就是一元二次方程的解，就是能够使方程左右两边相等的未知数的值．即用这个数代替未知数所得式子仍然成立．

解答：解：因为x=3是原方程的根，所以将x=3代入原方程，即32﹣3k﹣6=0成立，解得k=1．

故选A．

点评：本题考查的是一元二次方程的根即方程的解的定义．　

5．（2013安顺）如图，已知AE=CF，∠AFD=∠CEB，那么添加下列一个条件后，仍无法判定△ADF≌△CBE的是（　　）

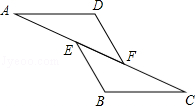
A．∠A=∠C B．AD=CB C．BE=DF D．AD∥BC

考点：全等三角形的判定．

分析：求出AF=CE，再根据全等三角形的判定定理判断即可．

解答：解：∵AE=CF，

∴AE+EF=CF+EF，

∴AF=CE，

A．∵在△ADF和△CBE中

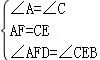
∴△ADF≌△CBE（ASA），正确，故本选项错误；

B．根据AD=CB，AF=CE，∠AFD=∠CEB不能推出△ADF≌△CBE，错误，故本选项正确；

C．∵在△ADF和△CBE中

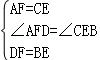
∴△ADF≌△CBE（SAS），正确，故本选项错误；

D．∵AD∥BC，

∴∠A=∠C，

∵在△ADF和△CBE中

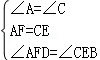
∴△ADF≌△CBE（ASA），正确，故本选项错误；

故选B．

点评：本题考查了平行线性质，全等三角形的判定的应用，注意：全等三角形的判定定理有SAS，ASA，AAS，SSS．　

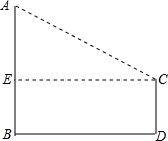
6．（2013安顺）如图，有两颗树，一颗高10米，另一颗高4米，两树相距8米．一只鸟从一颗树的树梢飞到另一颗树的树梢，问小鸟至少飞行（　　）

A．8米 B．10米 C．12米 D．14米

考点：勾股定理的应用．

专题：应用题．

分析：根据“两点之间线段最短”可知：小鸟沿着两棵树的树梢进行直线飞行，所行的路程最短，运用勾股定理可将两点之间的距离求出．

解答：解：如图，设大树高为AB=10m，

小树高为CD=4m，

过C点作CE⊥AB于E，则EBDC是矩形，

连接AC，

∴EB=4m，EC=8m，AE=AB﹣EB=10﹣4=6m，

在Rt△AEC中，AC=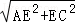=10m，

故选B．

点评：本题考查正确运用勾股定理．善于观察题目的信息是解题以及学好数学的关键．　

7．（2013安顺）若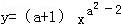是反比例函数，则a的取值为（　　）

A．1 B．﹣l C．±l D．任意实数

考点：反比例函数的定义．

专题：探究型．

分析：先根据反比例函数的定义列出关于a的不等式组，求出a的值即可．

解答：解：∵此函数是反比例函数，

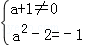∴，解得a=1．

故选A．

点评：本题考查的是反比例函数的定义，即形如y=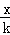（k为常数，k≠0）的函数称为反比例函数．　

8．（2013安顺）下列各数中，3.14159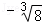，，0.131131113…，﹣π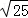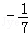，，，无理数的个数有（　　）

A．1个 B．2个 C．3个 D．4个

考点：无理数．

专题：常规题型．

分析：无限不循环小数为无理数，由此可得出无理数的个数．

解答：解：由定义可知无理数有：0.131131113…，﹣π，共两个．

故选B．

点评：此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．　

9．（2013安顺）已知一组数据3，7，9，10，x，12的众数是9，则这组数据的中位数是（　　）

A．9 B．9.5 C．3 D．12

考点：众数；中位数．

专题：计算题．

分析：先根据众数是一组数据中出现次数最多的数据，求得x，再由中位数要把数据按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数．

解答：解：∵众数是9，

∴x=9，

从小到大排列此数据为：3，7，9，9，10，12，

处在第3、4位的数都是9，9为中位数．

所以本题这组数据的中位数是9．

故选A．

点评：本题属于基础题，考查了确定一组数据的中位数和众数的能力．一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意找中位数的时候一定要先排好顺序，然后再根据奇数和偶数个来确定中位数，如果数据有奇数个，则正中间的数字即为所求，如果是偶数个则找中间两位数的平均数．　

10．（2013安顺）如图，A、B、C三点在⊙O上，且∠AOB=80°，则∠ACB等于（　　）

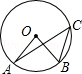
A．100° B．80° C．50° D．40°

考点：圆周角定理．

分析：由圆周角定理知，∠ACB=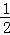∠AOB=40°．

解答：解：∵∠AOB=80°

∴∠ACB=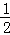∠AOB=40°．

故选D．

点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．　

二．填空题（共8小题，每小题4分，共32分）

11．（2013安顺）计算：﹣++= ．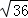

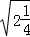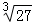考点：实数的运算．

专题：计算题．

分析：本题涉及二次根式，三次根式化简等考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．

解答：解：﹣++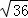

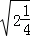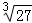
=﹣6+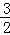+3

=﹣．

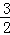故答案为﹣．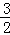

点评：本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握负整数指数幂、零指数幂、二次根式、绝对值等考点的运算．　

12．（2013安顺）分解因式：2a3﹣8a2+8a= ．

考点：提公因式法与公式法的综合运用．

分析：先提取公因式2a，再对余下的多项式利用完全平方公式继续分解．

解答：解：2a3﹣8a2+8a，

=2a（a2﹣4a+4），

=2a（a﹣2）2．

故答案为：2a（a﹣2）2．

点评：本题考查了用提公因式法和公式法进行因式分解，一个多项式有公因式首先提取公因式，然后再用其他方法进行因式分解，同时因式分解要彻底，直到不能分解为止．　

13．（2013安顺）4xa+2b﹣5﹣2y3a﹣b﹣3=8是二元一次方程，那么a﹣b= ．

考点：二元一次方程的定义；解二元一次方程组．

分析：根据二元一次方程的定义即可得到x、y的次数都是1，则得到关于a，b的方程组求得a，b的值，则代数式的值即可求得．

解答：解：根据题意得：，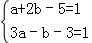

解得：．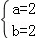

则a﹣b=0．

故答案是：0．

点评：主要考查二元一次方程的概念，要求熟悉二元一次方程的形式及其特点：含有2个未知数，未知数的项的次数是1的整式方程．　

14．（2013安顺）在Rt△ABC中，∠C=90°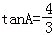，，BC=8，则△ABC的面积为 ．

考点：解直角三角形．

专题：计算题．

分析：根据tanA的值及BC的长度可求出AC的长度，然后利用三角形的面积公式进行计算即可．

解答：解：∵tanA==，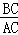

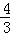∴AC=6，

∴△ABC的面积为×6×8=24．

故答案为：24．

点评：本题考查解直角三角形的知识，比较简单，关键是掌握在直角三角形中正切的表示形式，从而得出三角形的两条直角边，进而得出三角形的面积．　

15．（2013安顺）在平行四边形ABCD中，E在DC上，若DE：EC=1：2，则BF：BE= ．

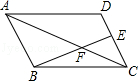
考点：相似三角形的判定与性质；平行四边形的性质．

分析：由题可知△ABF∽△CEF，然后根据相似比求解．

解答：解：∵DE：EC=1：2

∴EC：CD=2：3即EC：AB=2：3

∵AB∥CD，

∴△ABF∽△CEF，

∴BF：EF=AB：EC=3：2．

∴BF：BE=3：5．

点评：此题主要考查了平行四边形、相似三角形的性质．　

16．（2013安顺）已知关于x的不等式（1﹣a）x＞2的解集为x＜，则a的取值范围是 ．

考点：解一元一次不等式．

分析：因为不等式的两边同时除以1﹣a，不等号的方向发生了改变，所以1﹣a＜0，再根据不等式的基本性质便可求出不等式的解集．

解答：解：由题意可得1﹣a＜0，

移项得，﹣a＜﹣1，

化系数为1得，a＞1．

点评：本题考查了同学们解简单不等式的能力，解答这类题学生往往在解题时不注意移项要改变符号这一点而出错．

解不等式要依据不等式的基本性质，在不等式的两边同时加上或减去同一个数整式不等号的方向不变；在不等式的两边同时乘以或除以同一个正数不等号的方向不变；在不等式的两边同时乘以或除以同一个负数不等号的方向改变．　

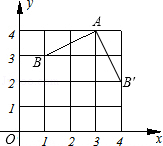
17．（2013安顺）如图，在平面直角坐标系中，将线段AB绕点A按逆时针方向旋转90°后，得到线段AB′，则点B′的坐标为 ．

考点：坐标与图形变化-旋转．

分析：画出旋转后的图形位置，根据图形求解．

解答：解：AB旋转后位置如图所示．

B′（4，2）．

点评：本题涉及图形旋转，体现了新课标的精神，抓住旋转的三要素：旋转中心A，旋转方向逆时针，旋转角度90°，通过画图得B′坐标．　

18．（2013安顺）直线上有2013个点，我们进行如下操作：在每相邻两点间插入1个点，经过3次这样的操作后，直线上共有 个点．

考点：规律型：图形的变化类．

分析：根据题意分析，找出规律解题即可．

解答：解：第一次：2013+（2013﹣1）=2×2013﹣1，

第二次：2×2013﹣1+2×2013﹣2=4×2013﹣3，

第三次：4×2013﹣3+4×2013﹣4=8×2013﹣7．

∴经过3次这样的操作后，直线上共有8×2013﹣7=16097个点．

故答案为：16097．

点评：此题主要考查了数字变化规律，根据已知得出点的变化规律是解题关键．　

三．解答题（共8小题，满分88分，解答应写出必要的文字说明或演算步骤）

19．（2013安顺）计算：2sin60°+2﹣1﹣20130﹣|1﹣|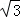

考点：实数的运算；零指数幂；负整数指数幂；特殊角的三角函数值．

专题：计算题．

分析：本题涉及零指数幂、特殊角的三角函数值、绝对值、负指数幂等四个考点．针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．

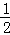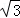解答：解：原式=2×+﹣1﹣（﹣1）=．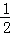

点评：本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此类题目的关键是熟记特殊角的三角函数值，熟练掌握零指数幂、特殊角的三角函数值、绝对值、负指数幂等考点的运算．　

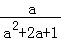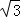20．（2013安顺）先化简，再求值：（1﹣）÷，其中a=﹣1．

考点：分式的化简求值．

专题：探究型．

分析：先根据整式混合运算的法则把原式进行化简，再把a的值代入进行计算即可．

解答：解：原式=÷

=×

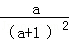
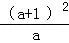
=a+1．

当a=﹣1时，原式=﹣1+1=．

点评：本题考查的是分式的混合运算，熟知分式混合运算的法则是解答此题的关键．　

21．（2013安顺）某市为进一步缓解交通拥堵现象，决定修建一条从市中心到飞机场的轻轨铁路．实际施工时，每月的工效比原计划提高了20%，结果提前5个月完成这一工程．求原计划完成这一工程的时间是多少月？

考点：分式方程的应用．

分析：设原来计划完成这一工程的时间为x个月，根据工程问题的数量关系建立方程求出其解即可．

解答：解：设原来计划完成这一工程的时间为x个月，由题意，得

，

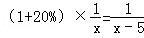解得：x=30．

经检验，x=30是原方程的解．

答：原计划完成这一工程的时间是30个月．

点评：本题考查了列分式方程解实际问题的运用，工作总量=工作效率×工作时间的运用，解答时根据工作效率的数量关系建立方程是解答的关键　

22．（2013安顺）已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A（﹣2，0），与反比例函数在第一象限内的图象的交于点B（2，n），连接BO，若S△AOB=4．

（1）求该反比例函数的解析式和直线AB的解析式；

（2）若直线AB与y轴的交点为C，求△OCB的面积．

考点：反比例函数综合题．

专题：计算题；待定系数法．

分析：（1）先由A（﹣2，0），得OA=2，点B（2，n），S△AOB=4，得OA•n=4，n=4，则点B的坐标是（2，4），把点B（2，4）代入反比例函数的解析式为y=，可得反比例函数的解析式为：y=；再把A（﹣2，0）、B（2，4）代入直线AB的解析式为y=kx+b可得直线AB的解析式为y=x+2．

（2）把x=0代入直线AB的解析式y=x+2得y=2，即OC=2，可得S△OCB=OC×2=×2×2=2．

解答：解：（1）由A（﹣2，0），得OA=2；

∵点B（2，n）在第一象限内，S△AOB=4，

∴OA•n=4；

∴n=4；

∴点B的坐标是（2，4）；

设该反比例函数的解析式为y=（a≠0），

将点B的坐标代入，得4=，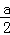

∴a=8；

∴反比例函数的解析式为：y=；

设直线AB的解析式为y=kx+b（k≠0），

将点A，B的坐标分别代入，得，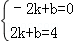

解得；

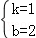∴直线AB的解析式为y=x+2；

（2）在y=x+2中，令x=0，得y=2．

∴点C的坐标是（0，2），

∴OC=2；

∴S△OCB=OC×2=×2×2=2．

点评：本题考查反比例函数和一次函数解析式的确定、图形的面积求法等知识及综合应用知识、解决问题的能力．此题有点难度．

23．（2013安顺）如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．

（1）求证：四边形BCFE是菱形；

（2）若CE=4，∠BCF=120°，求菱形BCFE的面积．

考点：菱形的判定与性质；三角形中位线定理．

分析：从所给的条件可知，DE是△ABC中位线，所以DE∥BC且2DE=BC，所以BC和EF平行且相等，所以四边形BCFE是平行四边形，又因为BE=FE，所以是菱形；∠BCF是120°，所以∠EBC为60°，所以菱形的边长也为4，求出菱形的高面积就可求．

解答：（1）证明：∵D、E分别是AB、AC的中点，

∴DE∥BC且2DE=BC，

又∵BE=2DE，EF=BE，

∴EF=BC，EF∥BC，

∴四边形BCFE是平行四边形，

又∵BE=FE，

∴四边形BCFE是菱形；

（2）解：∵∠BCF=120°，

∴∠EBC=60°，

∴△EBC是等边三角形，

∴菱形的边长为4，高为2，

∴菱形的面积为4×2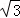=8．

点评：本题考查菱形的判定和性质以及三角形中位线定理，以及菱形的面积的计算等知识点．　

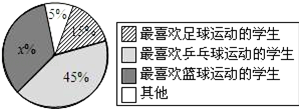
24．（2013安顺）某校一课外活动小组为了解学生最喜欢的球类运动情况，随机抽查本校九年级的200名学生，调查的结果如图所示．请根据该扇形统计图解答以下问题：（1）求图中的x的值；

（2）求最喜欢乒乓球运动的学生人数；

（3）若由3名最喜欢篮球运动的学生，1名最喜欢乒乓球运动的学生，1名最喜欢足球运动的学生组队外出参加一次联谊活动．欲从中选出2人担任组长（不分正副），列出所有可能情况，并求2人均是最喜欢篮球运动的学生的概率．

考点：扇形统计图；概率公式．

专题：图表型．

分析：（1）考查了扇形图的性质，注意所有小扇形的百分数和为1；

（2）根据扇形图求解，解题的关键是找到对应量：最喜欢乒乓球运动的学生人数对应的百分比为x%；

（3）此题可以采用列举法，注意要做到不重不漏．

解答：解：（1）由题得：x%+5%+15%+45%=1，

解得：x=35．（2分）

（2）最喜欢乒乓球运动的学生人数为200×45%=90（人）．（4分）

（3）用A1，A2，A3表示3名最喜欢篮球运动的学生，B表示1名最喜欢乒乓球运动的学生，C表示1名喜欢足球运动的学生，则从5人中选出2人的情况有：（A1，A2），（A1，A3），（A1，B），（A1，C），（A2，A3），（A2，B），（A2，C），（A3，B），（A3，C），（B，C），共计10种．（6分）

选出的2人都是最喜欢篮球运动的学生的有（A1，A2），（A1，A3），（A2，A3）共计3种，（7分）

则选出2人都最喜欢篮球运动的学生的概率为．（9分）

点评：此题考查了扇形图与概率的知识，综合性比较强，解题时要注意认真审题，理解题意；在用列举法求概率时，一定要注意不重不漏．用到的知识点为：概率=所求情况数与总情况数之比．　

25．（2013安顺）如图，AB是⊙O直径，D为⊙O上一点，AT平分∠BAD交⊙O于点T，过T作AD的垂线交AD的延长线于点C．

（1）求证：CT为⊙O的切线；

（2）若⊙O半径为2，CT=，求AD的长．

考点：切线的判定与性质；勾股定理；圆周角定理．

分析：（1）连接OT，根据角平分线的性质，以及直角三角形的两个锐角互余，证得CT⊥OT，CT为⊙O的切线；

（2）证明四边形OTCE为矩形，求得OE的长，在直角△OAE中，利用勾股定理即可求解．

解答：（1）证明：连接OT，

∵OA=OT，

∴∠OAT=∠OTA，

又∵AT平分∠BAD，

∴∠DAT=∠OAT，

∴∠DAT=∠OTA，

∴OT∥AC，（3分）

又∵CT⊥AC，

∴CT⊥OT，

∴CT为⊙O的切线；（5分）

（2）解：过O作OE⊥AD于E，则E为AD中点，

又∵CT⊥AC，

∴OE∥CT，

∴四边形OTCE为矩形，（7分）

∵CT=，

∴OE=，

又∵OA=2，

∴在Rt△OAE中，，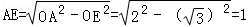

∴AD=2AE=2．（10分）

点评：本题主要考查了切线的判定以及性质，证明切线时可以利用切线的判定定理把问题转化为证明垂直的问题．　

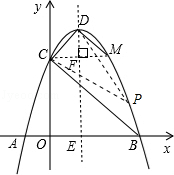
26．（2013安顺）如图，已知抛物线与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C（0，3）．

（1）求抛物线的解析式；

（2）设抛物线的顶点为D，在其对称轴的右侧的抛物线上是否存在点P，使得△PDC是等腰三角形？若存在，求出符合条件的点P的坐标；若不存在，请说明理由；

（3）点M是抛物线上一点，以B，C，D，M为顶点的四边形是直角梯形，试求出点M的坐标．

考点：二次函数综合题．

专题：压轴题．

分析：（1）由于A（﹣1，0）、B（3，0）、C（0，3）三点均在坐标轴上，故设一般式解答和设交点式（两点式）解答均可．

（2）分以CD为底和以CD为腰两种情况讨论．运用两点间距离公式建立起P点横坐标和纵坐标之间的关系，再结合抛物线解析式即可求解．

（3）根据抛物线上点的坐标特点，利用勾股定理求出相关边长，再利用勾股定理的逆定理判断出直角梯形中的直角，便可解答．

解答：解：（1）∵抛物线与y轴交于点C（0，3），

∴设抛物线解析式为y=ax2+bx+3（a≠0），

根据题意，得，

解得，

∴抛物线的解析式为y=﹣x2+2x+3．

（2）存在．

由y=﹣x2+2x+3得，D点坐标为（1，4），对称轴为x=1．

①若以CD为底边，则PD=PC，

设P点坐标为（x，y），根据两点间距离公式，

得x2+（3﹣y）2=（x﹣1）2+（4﹣y）2，

即y=4﹣x．

又P点（x，y）在抛物线上，

∴4﹣x=﹣x2+2x+3，

即x2﹣3x+1=0，

解得x1=，x2=＜1，应舍去，

∴x=，

∴y=4﹣x=，

即点P坐标为．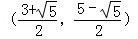

②若以CD为一腰，

∵点P在对称轴右侧的抛物线上，由抛物线对称性知，点P与点C关于直线x=1对称，

此时点P坐标为（2，3）．

∴符合条件的点P坐标为或（2，3）．

（3）由B（3，0），C（0，3），D（1，4），根据勾股定理，

得CB=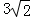，CD=，BD=，

∴CB2+CD2=BD2=20，

∴∠BCD=90°，

设对称轴交x轴于点E，过C作CM⊥DE，交抛物线于点M，垂足为F，在Rt△DCF中，

∵CF=DF=1，

∴∠CDF=45°，

由抛物线对称性可知，∠CDM=2×45°=90°，点坐标M为（2，3），

∴DM∥BC，

∴四边形BCDM为直角梯形，

由∠BCD=90°及题意可知，

以BC为一底时，顶点M在抛物线上的直角梯形只有上述一种情况；

以CD为一底或以BD为一底，且顶点M在抛物线上的直角梯形均不存在．

综上所述，符合条件的点M的坐标为（2，3）．

点评：此题是一道典型的“存在性问题”，结合二次函数图象和等腰三角形、等腰梯形的性质，考查了它们存在的条件，有一定的开放性．