(单词翻译:单击)
第1卷 (选择题 共3 6分)
一、选择题(本题共1 2小题,在每个小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来,每小题选对得3分,选错、不选或选出的答案超过一个均记O分.)
1.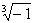 的立方根是( )
的立方根是( )
A.-1 B.O C.1 D. ±1
2.下列标志中不是中心对称图形的是( )
3.下列实数中是无理数的是(
 )
)
A.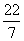 B.2-2 c.
B.2-2 c.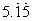 D.sin450
D.sin450
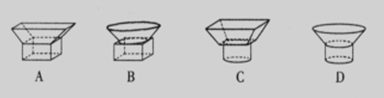
4.一个几何体的三视图如右图所示,则该几何体是( )
5.若代数式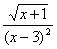 有意义,则实数x的取值范围是( )
有意义,则实数x的取值范围是( )
A.x≥一1 B.x≥一1且x≠3 C.x>-l D.x>-1且x≠3
6.如图,平行四边形ABCD的顶点A、B、D在⊙0上,顶点C在⊙0的直径BE上,连接AE,∠E=360,,则∠ADC的度数是( )
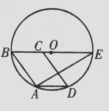
A,440 B.540 C.720 D.530
7. 若不等式组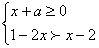 无解,则实数a的取值范围是( )
无解,则实数a的取值范围是( )
A.a≥一1 B.a<-1 C.a≤1 D.a≤-1
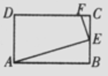
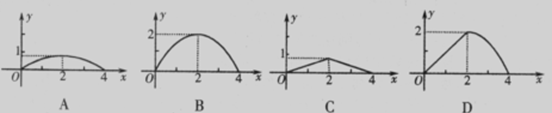
8.如图,已知矩形ABCD的长AB为5,宽BC为4.E是BC边上的一个动点,AE⊥上EF,EF交CD于点F.设BE=x,FC=y,则点 E从点B运动到点C时,能表示y关于x的函数关系的大致图象是
9.等腰三角形一条边的边长为3,它的另两条边的边长是关于x的一元二次方程x2 -12x+k=O的两个根,则k的值是( )
A:27 B:36 C:27或36 D:18
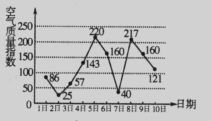
10. 右图是某市7月1日至1 0日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于2 00表示空气重度污染,某人随机选择7月1日至7月8日中的某一天到达该市,并连续停留3天 .则此人在该市停留期间有且仅有
.则此人在该市停留期间有且仅有 1天空气质量优良的概率是( )
1天空气质量优良的概率是( )
A 、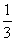 B、
B、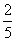 C、
C、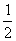 D、
D、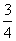
11.已知一次函数y1=kx+b(k<O)与反比例函数y2=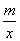 (m≠O)的图象相交于A、B两点,其横坐标分别是-1和3,当y1>y2时,实数x的取值范围是( )
(m≠O)的图象相交于A、B两点,其横坐标分别是-1和3,当y1>y2时,实数x的取值范围是( )
A.x<-l或O<x<3 B.一1<x<O或O<x<3 C.一1<x<O或x>3 D.O<x<3
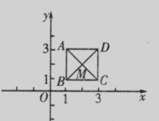
12,如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换.如此这样,连续经过2014次变换后,正方形ABCD的对角线交点M的坐标变为 ( )
A.(—2012,2) B.(一2012,一2)
C. (—2013,—2) D. (—2013,2)
第Ⅱ卷 (非选择题 共84分)
二、填空题(本大题共6小题,共1 8分,只要求填写最后结果,每小题填对得3分)
13.分解因式:2x(x-3)一8= ______________ .
14.计算:82014×(一0.125)2015= ___________.
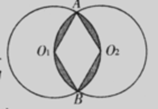
15.如图,两个半径均为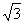 的⊙O1与⊙O2相交于A、B两点,且每个圆都经过另一个圆的圆心,则图中阴影部分的面积为___________.(结果保留π)
的⊙O1与⊙O2相交于A、B两点,且每个圆都经过另一个圆的圆心,则图中阴影部分的面积为___________.(结果保留π)
16.已知一组数据一3,x,一2, 3,1,6的中位数为1,则其方差为____________.
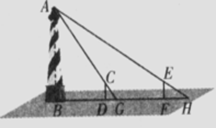
17.如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的CD和EF,两标杆相隔
52米,并且建筑物AB、标杆CD和EF在同一竖直平面内,从标杆CD后退2米到点G处,在G处测得建筑物顶端A和标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一条直线上,则建筑物的高是_____________米.
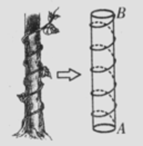
18。我国古代有这样一道数学问题:“枯木一根直立地上'高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?,题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是_________尺.
三、解答题(本大题共6小题,共66分,解答要写出必 要的文字说明、证明算步骤.)
要的文字说明、证明算步骤.)
19.(本小题满分9分)
今年我市把男生“引体向上”项目纳入学业水平体育考试内容.考试前某校为了解该项目的整体水平,从九年级220名男生中,随机抽取20名进行“引体向上”测试成绩(单位:个)如下:
9 12 3 13 18 8 8 4 ■ ,12
13 12 9 8 12 13 18 13 12 10
其中有一数据被污损,统计员只记得11.3是这组样本数据的平均数.
(1)求该组样本数据中被污损的数据和这组数据 的极差;
的极差;
(2)请补充完整下面的频数、频率分布表和频数分布直方图;
(3)估计在学业水平体育考试中该校九年级有多少名男生能完成11个以上(包含11个)“引体向上”?
20.(本小题满分1 0分)
如图,在梯形ABCD中,AD∥BC,∠B=900,以AB为直径作⊙O,恰与另一腰CD相切于点E,连接OD、OC、BE.
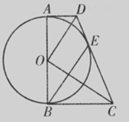
(1)求证:OD∥BE;
(2)若梯形ABCD的面积是48,设OD=x,OC=y,且x+y=14,
求CD的长.
21.(本小题满分10分)
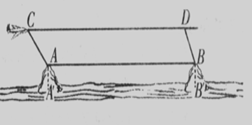
如图,某海域有两个海拔均为200米的海岛A和海岛B,一勘测飞机在距离海平面垂直高度为1100米的空中飞行,飞行到点C处时测得正前方一海岛顶端A的俯角是450,然后:沿平行于AB的方向水平飞行1.99×104米到
达点D处,在D处测得正前方另一海岛顶端B 的俯角是600,求两海岛间的距离AB.
22.(本小题满分1 2分)
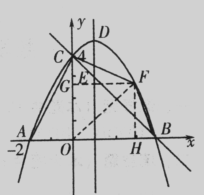
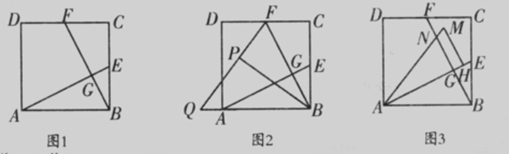
如图1,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE、BF,交点为G.
(1)求证:AE⊥BF;
(2)将△BCF沿BF对折,得到△BPF(如图2),延长FP交BA的延长线于点Q,求sin∠BQP的值;
(3)将△ABE绕点A逆时针方向旋转,使边AB正好落在AE上,得到△AHM(如图3),若AM和BF相交于点N,当正方形ABCD的面积为4时,求四边形GHMN的面积.
23、(本小题满分12分)
经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)
的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为O千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时.研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.
(1)求大桥上车流密度为100辆/千米时的车流速度.
(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时时,应控制大桥上的车流密度在什么范围内?
(3)车流量(辆/小时)是 单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.
单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.
24.(本小题满分13分)
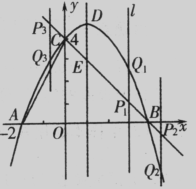
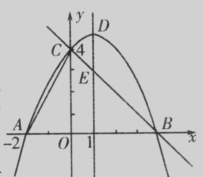
如图,抛物线y=ax2+bx+c(a≠O)与y轴交于点C(O,4),与x轴交于点A和点B,其中点A的坐标为(-2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
(3)平行于DE的一条动直线Z 与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标。
与直线BC相交于点P,与抛物线相交于点Q,若以D、E、P、Q为顶点的四边形是平行四边形,求点P的坐标。
2 0 1 4年潍坊市初中学业水平考试
数学试题(A)参考答案及评分标准
一、选择题(本题共12小题,每小题选对得3分,共36分.)
CCDDB BDABC AA
二、填空题(本大题共6小题,每小题填对得3分,共1 8分.)
13. 2(x+l)(x-4) 14.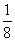 15.
15.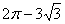
16. 9 17. 54 18. 25
三、解答题(本大题共6小题,共6 6分.)
1 9.(本小题满分9分)
解:(1)设被污损的数据为x,
由题意知: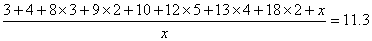 .....1分
.....1分
解得:x=19 ................2分
根据极差的定义,可得该组数据的极差是19-3=16. ……………………………3分
(2)由样本数据知,
测试成绩在6~10个的有6名,该组频数为6,相应频率是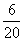 =o.30;
=o.30;
测试成绩在11~15个的有9名,该组频数为9,相应频率是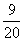 =0.45.
=0.45.
补全的频数、频率分布表和频数分布直方图如下所示:
(3)由频率分布表可知,能完成_11个以上的是后两组,(0.45 +0.15)×100%=60%,
由此估计在学业水平体育考试中能完成11个以上“引体向上’的男生数是
220×60% =132(名) ...........................9分
20.(本小题满分1 0分)
(1)证明:连接OE,
∵CD是⊙O的切线, ∴OE⊥CD:),.........1分
在Rt△OAD和Rt△OED中,OA=OE, OD=OD,
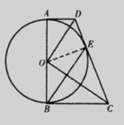
∴Rt△OADcR≌t△OED, ∴∠AOD=∠EOD= ∠AOE,...................2分
∠AOE,...................2分
在⊙O中,ABE=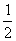 ∠AOE, ∴∠AOD=∠ABE, ....................3分
∠AOE, ∴∠AOD=∠ABE, ....................3分
∴OD∥BE ..................4分
(2)同理可证:Rt△COE≌Rt△COB.∴∠COE=∠COB=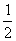 ∠BOE,
∠BOE,
∴∠DOE+∠COE=900,∴△COD是直角三角形, ………………5分
∵S△DEO=S△DAO, S△COE=S△COB,
∴S梯形ABCD =2(S△DOE+S△COE)=2S△COD=OC·OD=48,即xy=48, .........7分
又∵x+y= 14,∴x2 +y2=(x+y)2-2xy=142-2×48=100,
在Rt△COD中,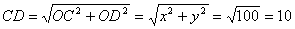 …………………9分
…………………9分
即CD的长为10. ……………1 0分
21.(本小题满分10分)
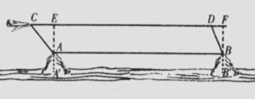
解:如图,过点A作AE⊥CD于点E,过点B作BF上CD,交CD的延长线于点F,则四边形ABFE为矩形,
所以AB=EF, AE=BF, ................2分
由题意可知AE=BF=1100—200=900,
CD=19900..................................3分.
∴在Rt△AEC中,∠C=450, AE=900,
∴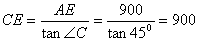 ............................5分
............................5分
在Rt△BFD中,∠BDF=600,BF=900, BF=900
∴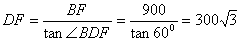 .........................7分
.........................7分
∴ AB=EF=CD+DF-CE=19900+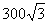 -900=19000+
-900=19000+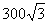 ……………9分
……………9分
答:两海岛之间的距离AB是 (19000+300√3)米 ................ .10分
(19000+300√3)米 ................ .10分
22.(本小题满分1 2分)
(1)证明:∵E、F分别是正方形ABCD边BC、CD的中点,∴CF=BE, ……1分
∵Rt△ABE≌Rt△BCF ∴∠BAE=∠CBF................................2分
又∵∠BAE+∠BEA=900,∴∠CBF+∠BEA=900,
∴∠BGE=900, ∴AE⊥BF ..... ...........................,.,...3分
(2)根据题意得:FP=FC,∠PFB=∠BFC,∠FPB=900, ……………………4分
∵CD∥AB, ∴∠CFB=∠ABF,∴∠ABF=∠PFB.∴QF=QB ……………5分
令PF=k(k>O),则PB=2k,
在Rt△BPQ中,设QB=x, ∴x2=(x-k)2+4k2, ∴x=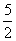 k,..................6分
k,..................6分
∴sin∠BQP=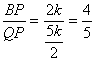 .........................7分
.........................7分
由题意得:∠BAE=∠EAM,又AE⊥BF, ∴AN=AB=2,...,,.,....,...,........8分
∵ ∠AHM=900, ∴GN//HM, . .........................................9分
∴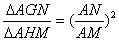 ∴
∴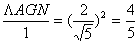 ...................10分
...................10分
∴ 四边形GHMN=SΔAHM - SΔAGN=1一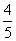 =
= 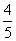 .................... 11分
.................... 11分
所以四边形GHMN的面积是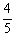 …………………………………12分
…………………………………12分
23.(本小题满分1 2分)
解:(1)由题意得:当20≤x≤220时,v是x的一次函数
则可设v=kx+b(k≠O), ...............................,...,.....1分
由题意得:当x=20时,v=80,当x=220时,v=0
所以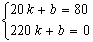 解得:
解得: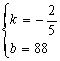 ,
,
所以当20≤x≤220时,v=-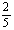 x+88 ,.........,.................4分
x+88 ,.........,.................4分
则当x=100时,y=一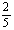 ×100+88=48.
×100+88=48.
即当大桥上车流密度为100辆/千米时,车流速度为48千米/小时.……………5分
(2)当20≤v≤220时,v=一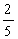 x+88(0≤v≤80),
x+88(0≤v≤80),
由题意得: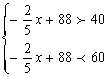 .解得70<x<120,
.解得70<x<120,
所以应控制车流密度的范围是大于70辆/千米且小于120辆/千米, ........7分
(3)①当0≤x≤20时,车流量y1=vx=80x,
因为k=80>0,,所以y1随x的增大面增大,
故当x=20时,车流量y1的最大值为1600. ……………………………………9分
②当20≤x≤220时,车流量y2=vx=(一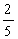 x+88)x=一(x-110)2+4840,
x+88)x=一(x-110)2+4840,
当x=110时,车流量y2取得最大值4840, ………………………………..1 0分
因为4840>1600,所以当车流密度是110辆/千米,车流量y取得最大值.....1 2分
24.(本小题满分1 3分)
解:(1)由抛物 线经过点C(O,4)可得c=4,①
线经过点C(O,4)可得c=4,①
∵对称轴x=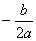 =1,∴b=-2a,②, . ..................,.]分
=1,∴b=-2a,②, . ..................,.]分
又抛物线过点A(一2,O)∴0=4a-2b+c,③ ……………………………………2分
由①②③ 解得:a=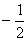 , b=1 ,c=4. ………………………………3分
, b=1 ,c=4. ………………………………3分
所以抛物线的解析式是y=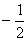 x+x+4
x+x+4
(2)假设存在满足条件的点F,如图如示,连接BF、CF、OF.
过点F分别作FH⊥x轴于H , FG⊥y轴于G.
设点F的坐标为(t, 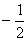 t2+t+4),
t2+t+4), 其中O<t<4,
其中O<t<4,
则FH=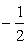 t2 +t+4 FG=t,
t2 +t+4 FG=t,
∴△OBF=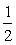 OB.FH=
OB.FH=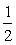 ×4×(
×4×(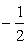 t2+4t+4)=一t2+2t+8 ………………5分
t2+4t+4)=一t2+2t+8 ………………5分
S△OFC=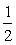 OC.FC=
OC.FC=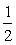 ×4×t=2t
×4×t=2t
∴S四边形ABFC—S△AOC+S△OBF +S△OFC=4-t2+2t+8+2t=-t2+4t+12.……6分
令一t2+4t+12 =17,即t2-4t+5=0,则△=(一4)2-4×5=一4<0,
∴方程t2 -4t+5=0无解,故不存在满足条件的点F.. …………7分
 (3)设直线BC的解析式为y=kx+b(k≠O),又过点B(4,0,), C(0,4)
(3)设直线BC的解析式为y=kx+b(k≠O),又过点B(4,0,), C(0,4)
所以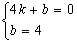 ,解得:
,解得: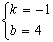 ,
,
所以直线BC的解析式是y=一x+4. . …………8分
由y=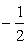 x2+4x+4=一
x2+4x+4=一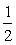 (x一1)2+
(x一1)2+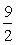 ,得D(1,
,得D(1,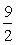 ), .
), .
又点E在直线BC上,则点E(1,3),
于是DE=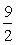 一3=
一3= 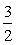
 .…………………9分
.…………………9分
若以D.E.P.Q为顶点的四边形是平行四边形,因为DE∥PQ,只须DE=PQ,......... …………………........10分
设点P的坐标是(m,一m+4),则点Q的坐标是(m,一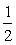 t2+m+4).
t2+m+4).
①当O<m<4时,PQ=(一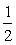 t2+m+4)一(一m+4)=一
t2+m+4)一(一m+4)=一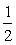 m2+2m.
m2+2m.
由一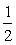 m2+2m=
m2+2m=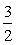 ,解得:m=1或3.当m=1时,线段PQ与DE重合,m=-1舍去,
,解得:m=1或3.当m=1时,线段PQ与DE重合,m=-1舍去,
∴m=-3,此时P1 (3,1). ..............11分
②当m<o或m>4时,PQ=(一m+4)一(一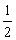 m2++m+4)=
m2++m+4)= 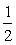 m2—2m,
m2—2m,
由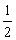 m2—2m=
m2—2m=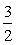 ,解得m=2±
,解得m=2±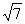 ,经检验适合题意,
,经检验适合题意,
此时P2(2+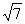 ,2一
,2一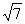 ),P3(2一
),P3(2一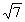 ,2+
,2+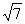 ).… .........12分.
).… .........12分.
综上所述,满足条件的点P有三个,分别是P1 (3,1),P2(2+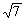 ,2 -
,2 -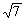 ),P3(2—
),P3(2—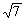 ,2十
,2十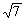 ). ..............1 3分
). ..............1 3分