(单词翻译:单击)
一、选择题(本大题共10小题,每小题4分,共40分.每小题只有一个正确的选项,请在答题卡的相应位置填涂)
1.(4分)﹣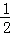 的倒数是( )
的倒数是( )
A. ﹣2 B. 2 C. ﹣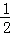 D.
D. 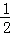
2.(4分)如图是由六个棱长为1的正方体组成的一个几何体,其主视图的面积是( )
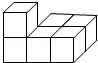
A. 3 B. 4 C. 5 D. 6
3.(4分)下列图形中,不是中心对称图形的是( )
A. 平行四边形 B. 矩形 C. 菱形 D. 等边三角形
4.(4分)如图,在△ABC中,AB=AC,DE∥BC,∠ADE=48°,则下列结论中不正确的是( )
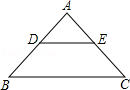
A. ∠B=48° B. ∠AED=66° C. ∠A=84° D. ∠B+∠C=96°
5.(4分)以下事件中,必然发生的是( )
A. 打开电视机,正在播放体育节目 B. 正五边形的外角和为180°
C. 通常情况下,水加热到100℃沸腾 D. 掷一次骰子,向上一面是5点
6.(4分)如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
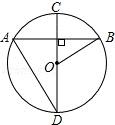
A. AD=AB B. ∠BOC=2∠D C. ∠D+∠BOC=90° D. ∠D=∠B
7.(4分)今年6月某日南![]() 平市各区县的最高气温(℃)如下表:
平市各区县的最高气温(℃)如下表:
区县 | 延平 | 建瓯 | 建阳 | 武夷山 | 浦城 | 松溪 | 政和 | 顺昌 | 邵武 | 光泽 |
气温(℃) | 33 | 32 | 32 | 30 | 30 | 29 | 29 | 31 | 30 | 28 |
则这10个区县该日最高气温的众数和中位数分别是( )
A. 32,32 B. 32,30 C. 30,30 D. 30,32
8.(4分)关于x的一元二次方程x2﹣2x+2+m2=0的根的情况是( )
A. 有两个不相等的实数根 B. 有两个相等的实数根
C. 没有实数根 D. 无法确定
9.(4分)给定一列按规律排列的数: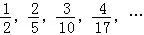 ,则这列数的第6个数是( )
,则这列数的第6个数是( )
A. 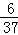 B.
B. 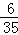 C.
C. 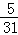 D.
D. 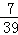
10.(4分)如图,Rt△ABC的顶点B在反比例函数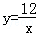 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是( )
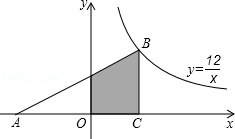
A. 12 B. 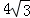 C.
C. 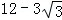 D.
D. 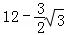
二、填空题(本大题共8小题,每小题3分,共24分.请将答案填入答题卡的相应位置)
11.(3分)计算: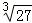 = 3 .
= 3 .
12.(3分)甲、乙、丙、丁四位同学在5次数学测验中,他们成绩的平均数相同,方差分别为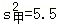 ,
,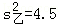 ,
,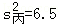 ,
,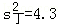 ,则成绩最稳定的同学是 丁 .
,则成绩最稳定的同学是 丁 .
13.(3分)写出一个第二象限内的点的坐标:( ﹣1 , 1 ).
14.(3分)分解因式:3a2+6a+3= 3(a+1)2 .
15.(3分)计算:(a2b)3= a6b3 .
16.(3分)长度分别为3cm,4cm,5cm,9cm的四条线段,任取其中三条能组成三角形的概率是 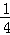 (或0.25) .
(或0.25) .
17.(3分)分式方程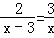 的解是 x=9 .
的解是 x=9 .
18.(3分)设点P是△ABC内任意一点.现给出如下结论:
①过点P至少存在一条直线将△ABC分成周长相等的两部分;
②过点P至少存在一条直线将△ABC分成面积相等的两部分;
③过点P至多存在一条直线将△ABC分成面积相等的两部分;
④△ABC内存在点Q,过点Q有两条直线将其平分成面积相等的四个部分.
其中结论正确的是 ①②④ .(写出所有正确结论的序号)
三、解答题(本大题共8小题,共86分.请在答题卡的相应位置作答)
19.(14分)
(1)计算: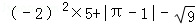 .
.
(2)化简: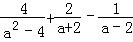 .
.
20.(8分)解不等式组: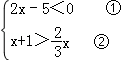 .
.
21.(8分)如图,在▱ABCD中,点E,F分别在BC,AD上,且BE=FD,求证:四边形AECF是平行四边形.
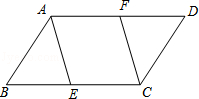
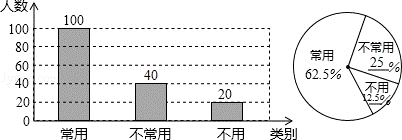
22.(10分)初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图:
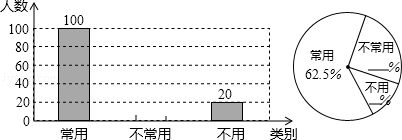
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是 160 ;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
23.(10分)某校为了实施“大课间”活动,计划购买篮球、排球![]() 共60个,跳绳120根.已知一个篮球70元,一个排球50元,一根跳绳10元.设购买篮球x个,购买篮球、排球和跳绳的总费用为y元.
共60个,跳绳120根.已知一个篮球70元,一个排球50元,一根跳绳10元.设购买篮球x个,购买篮球、排球和跳绳的总费用为y元.
(1)求y与x之间的函数关系式;
(2)若购买上述体育用品的总费用为4 700元,问篮球、排球各买多少个?
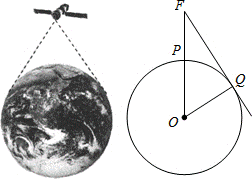
24.(10分)2013年6月11日,“神舟”十号载人航天飞船发射成功!如图,飞船完成变轨后,就在离地球(⊙O)表面约350km的圆形轨道上运行.当飞船运行到某地(P点)的正上方(F点)时,从飞船上能看到地球表面最远的点Q(FQ是⊙O的切线).已知地球的半径约为6 400km.求:
(1)∠QFO的度数;(结果精确到0.01°)
(2)地面上P,Q两点间的距离(PQ的长).
(π取3.142,结果保留整数)
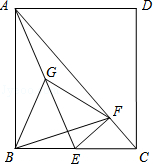
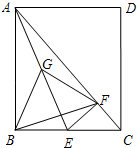
25.(12分)在矩形ABCD中,点E在BC边上,过E作EF⊥AC于F,G为线段AE的中点,连接BF、FG、GB.设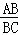 =k.
=k.
(1)证明:△BGF是等腰三角形;
(2)当k为何值时,△BGF是等边三角形?
(3)我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.事实上,在一个三角形中,较大的边所对的角也较大;反之也成立.
利用上述结论,探究:当△BGF分别为锐角、直角、钝角三角形时,k的取值范围.
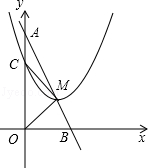
26.(14分)如图,已知点![]() A(0,4),B(2,0).
A(0,4),B(2,0).
(1)求直线AB的函数解析式;
(2)已知点M是线段AB上一动点(不与点A、B重合),以M为顶点的抛物线y=(x﹣m)2+n与线段OA交于点C.
①求线段AC的长;(用含m的式子表示)
②是否存在某一时刻,使得△ACM与△AMO相似?若存在,求出此时m的值.
一、选择题(本大题共10小题,每小题4分,共40分.每小题只有一个正确的选项,请在答题卡的相应位置填涂)
1.A
2.B
3.D
4.B
5.C
6.B
7.C
8.C
9.A
10.D
二、填空题(本大题共8小题,每小题3分,共24分.请将答案填入答题卡的相应位置)
11. 3 .
12. 丁 .
13.( ﹣1 , 1 ).
14. 3(a+1)2 .
15. a6b3 .
16. 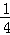 (或0.25) .
(或0.25) .
17. x=9 .
18. ①②④ .
三、解答题(本大题共8小题,共86分.请在答题卡的相应位置作答)
19.解:(1)原式=4×5+(π﹣1)﹣3=20+π﹣1﹣3=16+π;
(2)原式=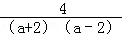 +
+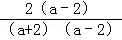 ﹣
﹣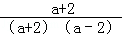 =
=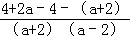 =
=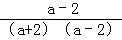 =
=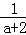 .
.
20.解:∵由①得:2x<5,
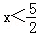 ,
,
由②得: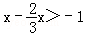 ,
,
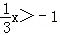 ,
,
x>﹣3,
∴不等式组的解集为 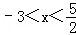 .
.
21.证明:在□ABCD中,AD=BC且AD∥BC
∵BE=FD,∴AF=CE
∴四边形AECF是平行四边形
22.解:
(1)100÷62.5%=160.即这次抽查的样本容量是160.故答案为160;
(2)不常用计算器的人数为:160﹣100﹣20=40;
不常用计算器的百分比为:40÷160=25%,
不用计算器的百分比为:20÷160=12.5%.
条形统计图和扇形统计图补全如下:
(3)∵“不常用”计算器的学生数为40,抽查的学生人数为160,
∴从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是: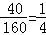 .
.
答:从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”的概率是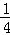 .
.
23.解:(1)依题意,得
y=70x+50(60﹣x)+10×120
=20x+4200;
(2)当 y=4700时,
4700=20x+4200(7分)
解得:x=25
∴排球购买:60﹣25=35(个)
答:篮球购买25个、排球购买35个.
24.解:(1)∵FQ是⊙O的切线,
∴OQ⊥FQ,
∴∠OQF=90°,
∴在Rt△OQF中,OQ=6400,OF=OP+PF=6400+350=6750,
∴sin∠QFO=\frac{OQ}{FQ}=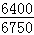 ≈0.9481,
≈0.9481,
∴∠QFO≈71.46°;
答:∠QFO的度数约为71.46°;
(2)∵∠QFO=71.46°,
∴∠FOQ=90°﹣71.46°=18.14°,
∴\widehat{PQ}的长=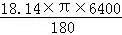 ≈2071,
≈2071,
答:地面上PP、Q两点间的距离约为2 071 km.
25.解:(1)证明:∵EF⊥AC于点F,
∴∠AFE=90°
∵在Rt△AEF中,G为斜边AE的中点,
∴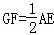 ,
,
在Rt△ABE中,同理可得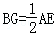 ,
,
∴GF=GB,
∴△BGF为等腰三角形;
(2)当△BGF为等边三角形时,∠BGF=60°
∵GF=GB=AG,
∴∠BGE=2∠BAE,∠FGE=2∠CAE
∴∠BGF=2∠BAC,
∴∠BAC=30°,
∴∠ACB=60°,
∴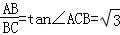 ,
,
∴当k=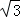 时,△BGF为等边三角形;
时,△BGF为等边三角形;
(3)由(1)得△BGF为等腰三角形,由(2)得∠BAC=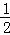 ∠BGF,
∠BGF,
∴当△BGF为锐角三角形时,∠BGF<90°,
∴∠BAC<45°,
∴AB>BC,
∴k=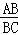 >1;
>1;
当△BGF为直角三角形时,∠BGF=90°,
∴∠BAC=45°
∴AB=BC,
∴k=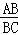 =1;
=1;
当△BGF为钝角三角形时,∠BGF>90°,
∴∠BAC>45°
∴AB<BC,
∴k=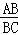 <1;
<1;
∴0<k<1.
26.解:(1)设直线AB的函数解析式为:y=kx+b.
∵点A坐标为(0,4),点B坐标为(2,0),
∴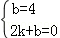 ,解得:
,解得: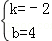 ,
,
即直线AB的函数解析式为y=﹣2x+4;
(2)①∵以M为顶点的抛物线为y=(x﹣m)2+n,
∴抛物线顶点M的坐标为(m,n).
∵点M在线段AB上,∴n=﹣2m+4,
∴y=(x﹣m)2﹣2m+4.
把x=0代入y=(x﹣m)2﹣2m+4,
得y=m2﹣2m+4,即C点坐标为(0,m2﹣2m+4),
∴AC=OA﹣OC=4﹣(m2﹣2m+4)=﹣m2+2m;
②存在某一时刻,能够使得△ACM与△AMO相似.理由如下:
过点M作MD⊥y轴于点D,则D点坐标为(0,﹣2m+4),
∴AD=OA﹣OD=4﹣(﹣2m+4)=2m.
∵M不与点A、B重合,∴0<m<2,
又∵MD=m,∴AM=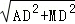 =
=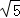 m.
m.
∵在△ACM与△AMO中,∠CAM=∠MAO,∠MCA>∠AOM,
∴当△ACM与△AMO相似时,假设△ACM∽△AMO,
∴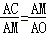 ,即
,即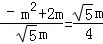 ,
,
整理,得 9m2﹣8m=0,解得m=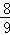 或m=0(舍去),
或m=0(舍去),
∴存在一时刻使得△ACM与△AMO相似,且此时m=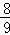 .
.