(单词翻译:单击)
第Ⅰ卷(选择题 共36分)
一、选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
1.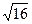 的算术平方根是( )
的算术平方根是( )
A. 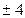 B. 4 C.
B. 4 C. 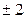 D. 2
D. 2
2.下列运算正确的是( )
A.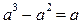 B.
B.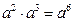
C.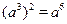 D.
D. 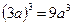
3.国家卫生和计划生育委员会公布H7N9禽流感病毒直径约为0.0000001m,则病毒直径0.0000001m用科学记数法表示为( )(保留两位有效数字).
A. 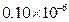 m B.
m B. 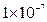 m
m
C. 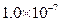 m D.
m D. 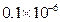 m
m
4.如图,已知AB∥CD,AD和BC相交于点O,∠A=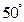 ,∠AOB=
,∠AOB=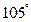 ,则∠C等于( )
,则∠C等于( )

A. 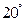 B.
B. 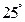 C.
C. 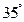 D.
D. 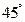
5.将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至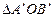 的位置,点B的横坐标为2,则点
的位置,点B的横坐标为2,则点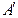 的坐标为( )
的坐标为( )
A.(1,1) B.(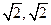 ) C.(-1,1) D.(
) C.(-1,1) D.(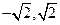 )
)
6.若定义: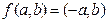 ,
,
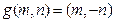 ,例如
,例如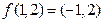 ,
,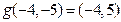 ,则
,则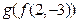 =( )
=( )
A.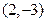 B.
B.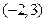 C.
C.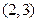 D.
D.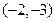
7.已知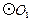 的半径
的半径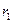 =2,
=2,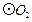 的半径
的半径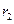 是方程
是方程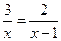 的根,
的根,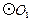 与
与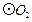 的圆心距为1,那么两圆的位置关系为( )
的圆心距为1,那么两圆的位置关系为( )
A.内含 B.内切 C.相交 D.外切
8.如图,正方形ABCD中,分别以B、D为圆心,以正方形的边长a为半径画弧,形成树叶形(阴影部分)图案,则树叶形图案的周长为( )

A. 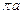 B.
B. 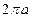
C. 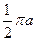 D
D .
. 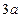
9.2013年“五·一”期间,小明与小亮两家准备从东营港、黄河入海口、龙悦湖中选择一景点游玩,小明与小亮通过抽签方式确定景点,则两家抽到同一景点的概率是( )
A. 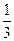 B.
B. 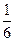 C.
C. 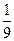 D.
D. 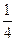
10.如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3、4及x,那么x的值( )
A. 只有1个 B. 可以有2个 C. 可以有3个 D. 有无数个
11.要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场),计划安排21场比赛,则参赛球队的个数是( )
A. 5个 B. 6个 C. 7个 D. 8个
12.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:
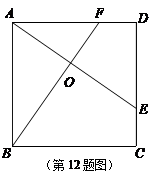
(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)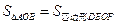 中正确的有( )
中正确的有( )
A. 4个 B. 3个 C. 2个 D. 1个
第Ⅱ卷(非选择题 共84分)
二、填空题:本大题共5小题,共20分,只要求填写最后结果,每小题填对得4分.
13.分解因式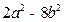 = .
= .
14.一组数据1,3,2,5,2,a的众数是a,这组数据的中位数是 
 .
.
15.某校研究性学习小组测量学校旗杆AB的高度,如图在教学楼一楼C处测得旗杆顶部的仰角为60°,在教学楼三楼D处测得旗杆顶部的仰角为30°,旗杆底部与教学楼一楼在同一水平线上,已知每层楼的高度为3米,则旗杆AB的高度为 米.
16.如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).
17.如图,已知直线l:y=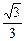 x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B
x,过点A(0,1)作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点A1;过点A1作y轴的垂线交直线l于点B1,过点B 1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 .
1作直线l的垂线交y轴于点A2;……按此作法继续下去,则点A2013的坐标为 .

三、解答题:本大题共7小题,共64 分.解答要写出必要的文字说明、证明过程或演算步骤.
分.解答要写出必要的文字说明、证明过程或演算步骤.
18. (本题满分7分,第⑴题3分,第⑵题4分)
(1)计算: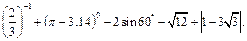
(2)先化简再计算: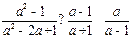 ,再选取一个你喜欢的数代入求值.
,再选取一个你喜欢的数代入求值.
19.(本题满分8分)东营市“创建文明城市”活动如火如荼的展开.某中学为了搞好“创城”活动的宣传,校学生会就本校学生对东营“市情市况”的了解程度进行了一次 调查测试.经过对测试成绩的分析,得到如下图所示的两幅不完整的统计图(A:59分及以下;B:60—69分;C:70—79分;D:80—89分;E:90—100分).请你
调查测试.经过对测试成绩的分析,得到如下图所示的两幅不完整的统计图(A:59分及以下;B:60—69分;C:70—79分;D:80—89分;E:90—100分).请你 根据图中提供的信息解答以下问题:
根据图中提供的信息解答以下问题:
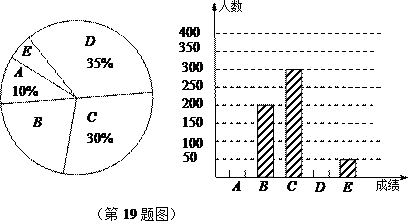
(1)求该校共有多少名学生;
(2)将条形统计图补充完整;
(3)在扇形统计图中,计算出“60—69分”部分所对应的圆心角的度数;
(4)从该校中任选一名学生,其测试成绩为“90—100分”的概率是多少?
20.(本题满分8分)如图,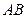 为
为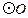 的直径,点
的直径,点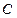 为
为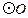 上一点,若
上一点,若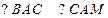 ,过点
,过点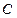 作直线
作直线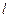 垂直于射线AM,垂足为点D.
垂直于射线AM,垂足为点D.
(1)试判断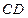 与
与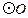 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若直线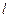 与
与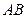 的延长线相交于点
的延长线相交于点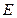 ,
, 的半径为3,并且
的半径为3,并且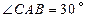 .求
.求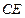 的长.
的长.

21.(本题满分9分)如图,在平 面直角坐标系中,一次函数
面直角坐标系中,一次函数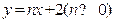 的图象与反比例函数
的图象与反比例函数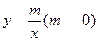 在第一象限内的图象交于点A,与x轴交于点B,线段OA=5,C为x轴正半轴上一点,且sin∠AOC=.
在第一象限内的图象交于点A,与x轴交于点B,线段OA=5,C为x轴正半轴上一点,且sin∠AOC=.

(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积.
22. (本题满分10分)在东营市中小学标准化建设工程中,某学校计划购进一批电脑和电子白板,经过市场考察得知,购买1台电脑和2台电子白板需要3.5万元,购买2台电脑和1台电子白板需要2.5万元.
(1)求每台电脑、每台电子白板各多少万元?
(2)根据学校实际,需购进电脑和电子白板共30台,总费用不超过30万元,但不低于28万元,请你通过计算求出有几 种购买方案,哪种方案费用最低.
种购买方案,哪种方案费用最低.
23.(本题满分10分) (1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=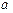 ,其中
,其中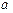 为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
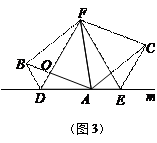
(3) 拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.

24.(本题满分12分) 已知抛物线y=ax2+bx+c的顶点A(2,0),与y轴的交点为B(0,-1).

(1)求抛物线的解析式;
(2)在对称轴右侧的抛物线上找出一点C,使以BC为 直径的圆经过抛物线的顶点A.并求出点
直径的圆经过抛物线的顶点A.并求出点 C的坐标以及此时圆的圆心P点的坐标.
C的坐标以及此时圆的圆心P点的坐标.
(3)在(2)的基础上,设直线x=t(0<t<10)与抛物线交于点N,当t为何值时,△BCN的面积最大,并求出最大值.
2013年东营市初中学生学业考试
数学试题参考答案与评分标准
一.选择题:本大题共12小题,在每小题给出的四个选项中,只有一项是正确的,请把正确的选项选出来.每小题选对得3分,选错、不选或选出的答案超过一个均记零分.
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
答案 | D | C | C | B | C | B | B | A | A | B | C | B |
二、填空题:本大题共5小题,共20分,只要求填写最后结果,每小题填对得4分.
13. 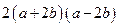 ; 14. 2; 15. 9; 16. 1.3;
; 14. 2; 15. 9; 16. 1.3;
17. 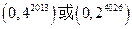 (注:以上两答案任选一个都对)
(注:以上两答案任选一个都对)
三、解答题:本大题共7小题,共64分.解答要写出必要的文字说明、证明过程或演算步骤.
18. (本题满分7分,第⑴题3分,第⑵题4分)
(1)解:
原式=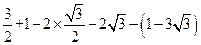
=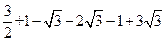
=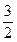 …………………………3分
…………………………3分
(2)解:
原式=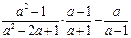
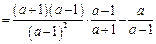
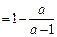
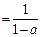 …………………………6分
…………………………6分
选取任意一个不等于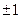 的
的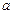 的值,代入求值.如:当
的值,代入求值.如:当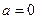 时,
时,
原式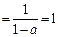 …………………………………7分
…………………………………7分
19. (本题满分8分)
解:(1)该学校的学生人数是: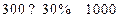 (人).………………………2分
(人).………………………2分
(2)条形统计图如图所示.………………………………………………………4分
(3)在扇形统计图中,“60—69分”部分所对应的圆心角的度数是:
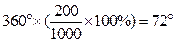 ………………………………………………………6分
………………………………………………………6分
(4)从该校中任选一名学生,其测试成绩为“90—100分”的概率是:
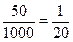 ………………………………………………………………8分
………………………………………………………………8分
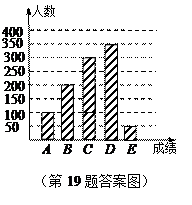 |
20. (本题满分8分)

(1)解:直线CD与⊙O相切. ………………1分
理由如下:连接OC.
∵OA=OC
∴∠BAC=∠OCA
∵∠BAC=∠CAM
∴∠OCA=∠CAM
∴OC∥AM…………………………3分
∵CD⊥AM
∴OC⊥CD
∴直线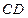 与
与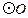 相切. …………………………5分
相切. …………………………5分
(2)解:
∵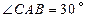
∴∠COE=2∠CAB=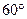
∴在Rt△COE中,OC=3,CE=OC·tan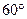 =
=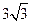 .…………………………8分
.…………………………8分
21. (本题满分9分)
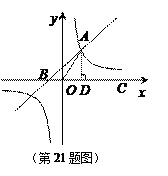
解:(1)过A点作AD⊥x轴于点D,
∵sin∠AOC==,OA=5
∴AD=4.
由勾股定理得:DO=3,
∵点A在第一象限
∴点A的坐标为(3,4)………………2分
将A的坐标为(3,4)代入y= ,得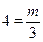 ,∴m=12
,∴m=12
∴该反比例函数的解析式为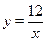 ………………4分
………………4分
将A的坐标为(3,4)代入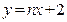 得:
得: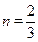
∴一次函数的解析式是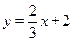 …………………………6分
…………………………6分
(2)在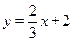 中,令y=0,即x+2=0,∴x=
中,令y=0,即x+2=0,∴x=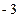
∴点B的坐标是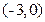
∴OB=3,又DA=4
∴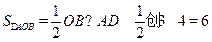 ,所以△AOB的面积为6.………9分
,所以△AOB的面积为6.………9分
22. (本题满分10分)
解:(1)设每台电脑x万元,每台电子白板y万元,根据题意得:
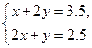 …………………………3分
…………………………3分
解得: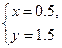 …………………………4分
…………………………4分
答:每台电脑0.5万元,每台电子白板1.5万元. …………………………5分
(2)设需购进电脑a台,则购进电子白板(30-a)台,
则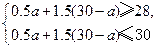 …………………………6分
…………………………6分
解得: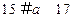 ,即a=15,16,17.…………………………7分
,即a=15,16,17.…………………………7分
故共有三种方案:
方案一:购进电脑15台,电子白板15台.总费用为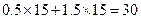 万元;
万元;
方案二:购进电脑16台,电子白板14台.总费用为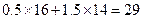 万元;
万元;
方案三:购进电脑17台,电子白板13台.总费用为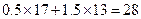 万元;
万元;
所以,方案三费用最低. …………………………10分
23. (本题满分10分)
证明:(1)∵BD⊥直线m,CE⊥直线m
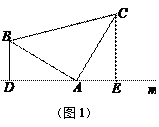
∴∠BDA=∠CEA=90°
∵∠BAC=90°
∴∠BAD+∠CAE=90°
∵∠BAD+∠ABD=90°
∴∠CAE=∠ABD………………1分
又AB=AC
∴△ADB≌△CEA………………2分
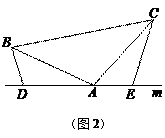
∴AE=BD,AD=CE
∴DE=AE+AD= BD+CE ………………3分
(2)∵∠BDA =∠BAC=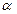 ,
,
∴∠DBA+∠BAD=∠BAD +∠CAE=180°—
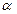
∴∠DBA=∠CAE………………4分
∵∠BDA=∠AEC=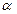 ,AB=AC
,AB=AC
∴△ADB≌△CEA………………5分
∴AE=BD,AD=CE
∴DE=AE+AD=BD+CE………………6分
(3)由(2)知,△ADB≌△CEA,
BD=AE, ∠DBA =∠CAE
∠DBA =∠CAE
∵△ABF和△ACF均为等边三角形
∴∠ABF=∠CAF=60°
∴∠DBA+∠ABF=∠CAE+∠CAF
∴∠DBF=∠FAE………………8分
∵BF=AF
∴△DBF≌△EAF………………9分
∴DF=EF,∠BFD=∠AFE
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°
∴△DEF为等边三角形.………………10分
24. (本题满分12分)
解:(1) ∵抛物线的顶点是A(2,0),设抛物线的解析式为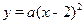 .
.
由抛物线过B(0,-1) 得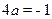 ,∴
,∴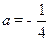 .……………………2分
.……………………2分
∴抛物线的解析式为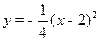 .
.
即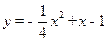 .………………………………3分
.………………………………3分

(2)设C的坐标为(x,y).
∵A在以BC为直径的圆上.∴∠BAC=90°.
作CD⊥x轴于D ,连接AB、AC.
则有 △AOB∽△CDA.………………………4分
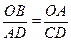
∴OB·CD=OA·AD.
即1·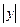 =2(x-2).∴
=2(x-2).∴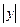 =2x-4.
=2x-4.
∵点C在第四象限.
∴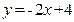 ………………………………5分
………………………………5分
由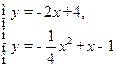 解得
解得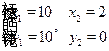 .
.
∵点C在对称轴右侧的抛物线上.
∴点C的坐标为 (10,-16).……………………6分

∵P为圆心,∴P为BC中点.
取OD中点H,连PH,则PH为梯形OBCD的中位线.
∴PH=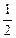 (OB+CD)=
(OB+CD)=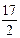 .……………………7分
.……………………7分
∵D(10,0)∴H (5,0)∴P (5, 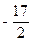 ).
).
故点P坐标为(5,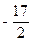 ).…………………………8分
).…………………………8分
(3)设点N的坐标为,直线x=t(0<t<10)与直线BC交于点M.
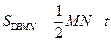 ,
,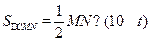
所以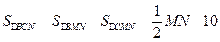 ………………………9分
………………………9分
设直线BC的解析式为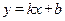 ,直线BC经过B(0,-1)、C (10,-16)
,直线BC经过B(0,-1)、C (10,-16)
所以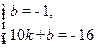 成立,解得:
成立,解得: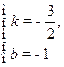 …………………………10分
…………………………10分
所以直线BC的解析式为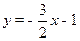 ,则点M的坐标为.
,则点M的坐标为.
MN==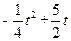 ………………………11分
………………………11分
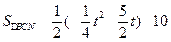
=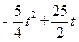 =
=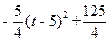
所以,当t=5时,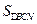 有最大值,最大值是
有最大值,最大值是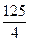 .…………………………12分
.…………………………12分


