(单词翻译:单击)
一、选择题(每小题3分,共24分)
1.(3分)(2013•长春)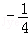 的绝对值等于( )
的绝对值等于( )
A. 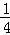 B. 4 C.
B. 4 C. 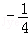 D. ﹣4
D. ﹣4
考点: 绝对值.
分析: 根据负数的绝对值等于它的相反数解答.
解答: 解:﹣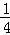 的绝对值等于
的绝对值等于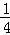 ,
,
即|﹣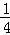 |=
|=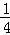 .
.
故选A.
点评: 本题考查了绝对值,一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.
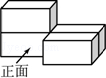
2.(3分)(2013•长春)如图是由四个相同的小长方体组成的立体图形,这个立体图形的正视图是( )
A.  B.
B.  C.
C.  D.
D. 
考点: 简单组合体的三视图.
分析: 找到从正面看所得到的图形即可,注意所有的看到的棱都应表现在主视图中.
解答: 解:从正面看易得第一层有1个长方形,位于左边,第二层有2个长方形.
故选D.
点评: 本题考查了三视图的知识,主视图是从物体的正面看得到的视图.
3.(3分)(2013•长春)我国第一艘航空母舰辽宁航空舰的电力系统可提供14 000 000瓦的电力.14 000 000这个数用科学记数法表示为( )
A. 14×106 B. 1.4×107 C. 1.4×108 D. 0.14×108
考点: 科学记数法—表示较大的数
分析: 科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值是易错点,由于14 000 000有8位,所以可以确定n=8﹣1=7.
解答: 解:14 000 000=1.4×107.
故选B.
点评: 此题考查科学记数法表示较大的数的方法,准确确定a与n值是关键.
4.(3分)(2013•长春)不等式2x<﹣4的解集在数轴上表示为( )
A.  B.
B.  C.
C.  D.
D. 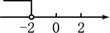
考点: 在数轴上表示不等式的解集;解一元一次不等式
分析: 首先解不等式求得不等式的解集,根据数轴上点的表示法即可判断.
解答: 解:解不等式得:x<﹣2.
故选D.
点评: 把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.
5.(3分)(2013•长春)如图,含30°角的直角三角尺DEF放置在△ABC上,30°角的顶点D在边AB上,DE⊥AB.若∠B为锐角,BC∥DF,则∠B的大小为( )
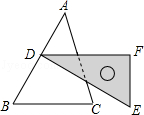
A. 30° B. 45° C. 60° D. 75°
考点: 平行线的性质;直角三角形的性质.
分析: 首先根据垂直定义可得∠ADE=90°,再根据∠FDE=30°,可得∠ADF=60°,然后根据两直线平行同位角相等可得∠B的大小.
解答: 解:∵DE⊥AB,
∴∠ADE=90°,
∵∠FDE=30°,
∴∠ADF=90°﹣30°=60°,
∵BC∥DF,
∴∠B=∠ADF=60°,
故选:C.
点评: 此题主要考查了平行线的性质,关键是掌握两直线平行同位角相等.
6.(3分)(2013•长春)如图,△ABC内接于⊙O,∠ABC=71°,∠CAB=53°,点D在AC弧上,则∠ADB的大小为( )
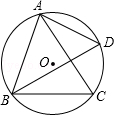
A. 46° B. 53° C. 56° D. 71°
考点: 圆周角定理.
分析: 根据三角形内角和定理求出∠ACB,根据圆周角定理得出∠C,求出即可.
解答: 解:∵∠ABC=71°,∠CAB=53°,
∴∠ACB=180°﹣∠ABC﹣∠BAC=56°,
∵弧AB对的圆周角是∠ADB和∠ACB,
∴∠ADB=∠ACB=56°,
故选C.
点评: 本题考查了圆周角定理和三角形内角和定理的应用,关键是求出∠ACB的度数和得出∠ACB=∠ADB.
7.(3分)(2013•长春)如图,∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,则CD的长为( )
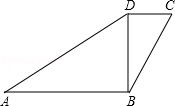
A. 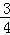 B.
B. 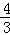 C. 2 D. 3
C. 2 D. 3
考点: 相似三角形的判定与性质.
专题: 探究型.
分析: 先根据题意判断出△ABD∽△BDC,再根据相似三角形的对应边成比例即可得出CD的长.
解答: 解:∵∠ABD=∠BDC=90°,∠A=∠CBD,AB=3,BD=2,
∴△ABD∽△BDC,
∴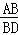 =
=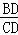 ,即
,即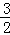 =
=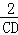 ,
,
解得CD=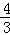 .
.
故选B.
点评: 本题考查的是相似三角形的判定与性质,熟知相似三角形的对应边成比例是解答此题的关键.
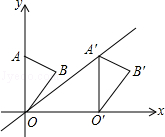
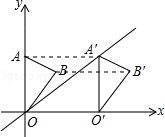
8.(3分)(2013•长春)如图,在平面直角坐标系中,点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,点A的对应点在直线y=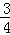 x上一点,则点B与其对应点B′间的距离为( )
x上一点,则点B与其对应点B′间的距离为( )
A. 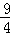 B. 3 C. 4 D. 5
B. 3 C. 4 D. 5
考点: 一次函数图象上点的坐标特征;坐标与图形变化-平移
分析: 根据平移的性质知BB′=AA′.由一次函数图象上点的坐标特征可以求得点A′的坐标,所以根据两点间的距离公式可以求得线段AA′的长度,即BB′的长度.
解答: 解:如图,连接AA′、BB′.
∵点A的坐标为(0,3),△OAB沿x轴向右平移后得到△O′A′B′,
∴点A′的纵坐标是3.
又∵点A的对应点在直线y=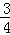 x上一点,
x上一点,
∴3=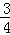 x,解得x=4.
x,解得x=4.
∴点A′的坐标是(4,3),
∴AA′=4.
∴根据平移的性质知BB′=AA′=4.
故选C.
点评: 本题考查了一次函数图象上点的坐标特征、坐标与图形变化﹣﹣平移.根据平移的性质得到BB′=AA′是解题的关键.
二、填空题(每小题3分,共18分)
9.(3分)(2013•长春)计算:a2•5a= 5a3 .
考点: 单项式乘单项式
专题: 计算题.
分析: 利用单项式乘单项式法则计算即可得到结果.
解答: 解:原式=5a3.
故答案为:5a3.
点评: 此题考查了单项式乘单项式,熟练掌握运算法则是解本题的关键.
10.(3分)(2013•长春)吉林广播电视塔“五一”假期第一天接待游客m人,第二天接待游客n人,则这2天平均每天接待游客 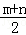 人(用含m、n的代数式表示).
人(用含m、n的代数式表示).
考点: 列代数式
分析: 用两天接待的游客总人数除以天数,即可得解.
解答: 解:2天平均每天接待游客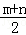 .
.
故答案为: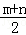 .
.
点评: 本题考查了列代数式,比较简单,熟练掌握平均数的求法是解题的关键.
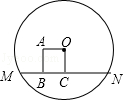
11.(3分)(2013•长春)如图,MN是⊙O的弦,正方形OABC的顶点B、C在MN上,且点B是CM的中点.若正方形OABC的边长为7,则MN的长为 28 .
考点: 垂径定理;正方形的性质.
分析: 根据正方形性质得出BC=7,∠OCB=90°,根据垂径定理得出CM=2BC,推出MN=4BC,代入求出即可.
解答: 解:∵四边形OABC是正方形,
∴BC=7,∠OCB=90°,
∴OC⊥MN,
∴由垂径定理得:MN=2CM,
∵点B是CM的中点,
∴CM=2BC,
∴MN=4BC=4×7=28,
故答案为:28.
点评: 本题考查了垂径定理和正方形性质的应用,关键是推出MN=4BC.
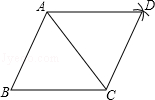
12.(3分)(2013•长春)如图,以△ABC的顶点A为圆心,以BC长为半径作弧;再以顶点C为圆心,以AB长为半径作弧,两弧交于点D;连结AD、CD.若∠B=65°,则∠ADC的大小为 65 度.
考点: 全等三角形的判定与性质.
分析: 根据作法可得AB=CD,BC=AD,然后利用“边边边”证明△ABC和△CDA全等,再根据全等三角形对应角相等解答.
解答: 解:∵以点A为圆心,以BC长为半径作弧;以顶点C为圆心,以AB长为半径作弧,两弧交于点D,
∴AB=CD,BC=AD,
在△ABC和△CDA中,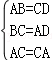 ,
,
∴△ABC≌△CDA,
∴∠ADC=∠B=65°.
故答案为:65.
点评: 本题考查了全等三角形的判定与性质,根据作法得到全等三角形相等的边是解题的关键.
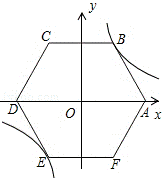
13.(3分)(2013•长春)如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数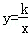 位于第一象限的图象上,则k的值为
位于第一象限的图象上,则k的值为 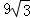 .
.
考点: 正多边形和圆;反比例函数图象上点的坐标特征.
分析: 连接OB,过B作BM⊥OA于M,得出等边三角形AOB,求出OB,根据锐角三角函数求出BM和OM,即可得出B的坐标,代入即可求出答案.
解答: 解: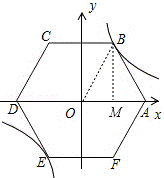
连接OB,过B作BM⊥OA于M,
∵六边形ABCDEF是正六边形,
∴∠AOB=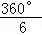 =60°,
=60°,
∵OA=OB,
∴△AOB是等边三角形,
∴OA=OB=AB=6,
∴BM=OB•sin∠BOA=6×sin60°=3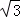 ,OM=OB•COS60°=3,
,OM=OB•COS60°=3,
即B的坐标是(3,3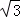 ),
),
∵B在反比例函数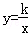 位于第一象限的图象上,
位于第一象限的图象上,
∴k=3×3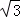 =9
=9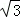 ,
,
故答案为:9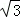 .
.
点评: 本题考查了正多边形性质,锐角三角函数,反比例函数的性质,等边三角形的性质和判定的应用,关键是求出B的坐标.
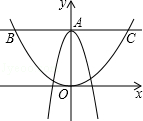
14.(3分)(2013•长春)如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=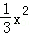 于点B、C,则BC的长值为 6 .
于点B、C,则BC的长值为 6 .
考点: 二次函数图象上点的坐标特征.
分析: 先由y轴上点的横坐标为0求出A点坐标为(0,3),再将y=3代入y=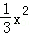 ,求出x的值,得出B、C两点的坐标,进而求出BC的长度.
,求出x的值,得出B、C两点的坐标,进而求出BC的长度.
解答: 解:∵抛物线y=ax2+3与y轴交于点A,
∴A点坐标为(0,3).
当y=3时,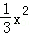 =3,
=3,
解得x=±3,
∴B点坐标为(﹣3,3),C点坐标为(3,3),
∴BC=3﹣(﹣3)=6.
故答案为6.
点评: 本题考查了二次函数图象上点的坐标特征,两函数交点坐标的求法,平行于x轴上的两点之间的距离,比较简单.
三、解答题(本大题共10小题,共78分)
15.(6分)(2013•长春)先化简,再求值: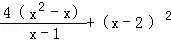 ,其中x=
,其中x=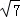 .
.
考点: 分式的化简求值
专题: 计算题.
分析: 将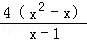 的分子因式分解,然后约分;再将(x﹣2)2展开,合并同类项后再代入求值即可.
的分子因式分解,然后约分;再将(x﹣2)2展开,合并同类项后再代入求值即可.
解答: 解:原式=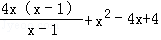
=4x+x2﹣4x+4
=x2+4.
当x=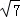 时,原式=
时,原式=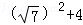 =11.
=11.
点评: 本题考查了分式的化简求值,熟悉因式分解及约分、通分是解题的关键.
16.(6分)(2013•长春)甲、乙两人各有一个不透明的口袋,甲的口袋中装有1个白球和2个红球,乙的口袋中装有2个白球和1个红球,这些球除颜色外其他都相同.甲、乙两人分别从各自口袋中随机摸出1个球,用画树状图(或列表)的方法,求两人摸出的球颜色相同的概率.
考点: 列表法与树状图法
专题: 计算题.
分析: 列表得出所有等可能的情况数,找出两人摸出的求颜色相同的情况数,即可求出所求的概率.
解答: 解:列表如下:
甲乙结果 白 红 红
白 (白,白) (红,白) (红,白)
白 (白,白) (红,白) (红,白)
红 (白,红) (红,红) (红,红)
所有等可能的情况有9种,其中颜色相同的情况有4种,
则P(两人摸出的球颜色相同)=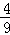 .
.
点评: 此题考查了列表法与树状图法,用到的知识点为:概率=所求情况数与总情况数之比.
17.(6分)(2013•长春)某班在“世界读书日”开展了图书交换活动,第一组同学共带图书24本,第二组同学共带图书27本.已知第一组同学比第二组同学平均每人多带1本图书,第二组人数是第一组人数的1.5倍.求第一组的人数.
考点: 分式方程的应用.
分析: 首先设第一组有x人,则第二组人数是1.5x人,根据题意可得等量关系:第一组同学共带图书24本÷第一组的人数﹣第二组同学共带图书27本÷第二组的人数=1,根据等量关系列出方即可.
解答: 解:设第一组有x人.
根据题意,得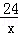 =
=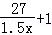 ,
,
解得x=6.
经检验,x=6是原方程的解,且符合题意.
答:第一组有6人.
点评: 此题主要考查了分式方程的应用,关键是正确理解题意,找出题目中的等量关系,列出方程,不要忘记检验.
18.(7分)(2013•长春)在△ABC中,AB=AC,点D、E、F分别是AC、BC、BA延长线上的点,四边形ADEF为平行四边形.求证:AD=BF.
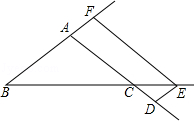
考点: 平行四边形的性质
专题: 证明题.
分析: 根据平行四边形的对边平行且相等可得AD=EF,AD∥EF,再根据两直线平行,同位角相等可得∠ACB=∠FEB,根据等边对等角求出∠ACB=∠B,从而得到∠FEB=∠B,然后根据等角对等边证明即可.
解答: 证明:∵四边形ADEF为平行四边形,
∴AD=EF,AD∥EF,
∴∠ACB=∠FEB,
∵AB=AC,
∴∠ACB=∠B,
∴∠FEB=∠B,
∴EF=BF,
∴AD=BF.
点评: 本题考查了平行四边形对边平行且相等的性质,平行线的性质,等角对等边的性质,熟练掌握各性质是解题的关键.
19.(7分)(2013•长春)如图,岸边的点A处距水面的高度AB为2.17米,桥墩顶部点C距水面的高度CD为23.17米.从点A处测得桥墩顶部点C的仰角为26°,求岸边的点A与桥墩顶部点C之间的距离.(结果精确到0.1米)(参考数据:sin26°=0.44,cos26°=0.90,tan26°=0.49)
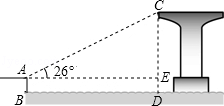
考点: 解直角三角形的应用-仰角俯角问题
分析: 在Rt△CAE中,利用CD、DE的长和已知的角的度数,利用正弦函数可求得AC的长.
解答: 解:由题意知,DE=AB=2.17,
∴CE=CD﹣DE=12.17﹣2.17=10.
在Rt△CAE中,∠CAE=26°,sin∠CAE=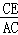 ,
,
∴AC=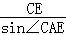 =
=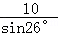 =
=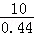 ≈22.7(米).
≈22.7(米).
答:岸边的点A与桥墩顶部点C之间的距离约为22.7米.
点评: 本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
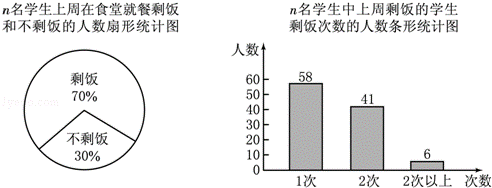
20.(7分)(2013•长春)某校学生会为了解学生在学校食堂就餐剩饭情况,随机对上周在食堂就餐的n名学生进行了调查,先调查是否剩饭的情况,然后再对其中剩饭的每名学生的剩饭次数进行调查.根据调查结果绘制成如下统计图.
(1)求这n名学生中剩饭学生的人数及n的值.
(2)求这n名学生中剩饭2次以上的学生占这n名学生人数的百分比.
(3)按上述统计结果,估计上周在学校食堂就餐的1 200名学生中剩饭2次以上的人数.
考点: 条形统计图;用样本估计总体;扇形统计图
专题: 计算题.
分析: (1)由条形统计图中的数据相加即可求出n名学生中剩饭的学生人数,除以剩饭学生所占的百分比即可求出学生的总数,即为n的值;
(2)根据条形统计图得到剩饭2次以上的人数,除以n的值,即可求出结果;
(3)根据(2)中求出的百分比,乘以1200即可得到结果.
解答: 解:(1)根据题意得:这n名学生中剩饭学生的人数为58+41+6=105(人),n的值为105÷70%=150,
则这n名学生中剩饭的学生有105人,n的值为150;
(2)根据题意得:6÷150×100%=4%,
则剩饭2次以上的学生占这n名学生人数的4%;
(3)根据题意得:1200×4%=48(人).
则估计上周在学校食堂就餐的1200名学生中剩饭2次以上的约有48人.
点评: 此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.
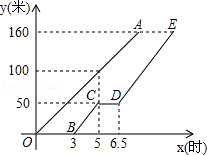
21.(8分)(2013•长春)甲、乙两工程队维修同一段路面,甲队先清理路面,乙队在甲队清理后铺设路面.乙队在中途停工了一段时间,然后按停工前的工作效率继续工作.在整个工作过程中,甲队清理完的路面长y(米)与时间x(时)的函数图象为线段OA,乙队铺设完的路面长y(米)与时间x(时)的函数图象为折线BC﹣CD﹣DE,如图所示,从甲队开始工作时计时.
(1)分别求线段BC、DE所在直线对应的函数关系式.
(2)当甲队清理完路面时,求乙队铺设完的路面长.
考点: 一次函数的应用
分析: (1)先求出乙队铺设路面的工作效率,计算出乙队完成需要的时间求出E的坐标,再由待定系数法就可以求出结论.
(2)由(1)的结论求出甲队完成的时间,把时间代入乙的解析式就可以求出结论.
解答: (1)设线段BC所在直线对应的函数关系式为y=k1x+b1.
∵图象经过(3,0)、(5,50),
∴
∴线段BC所在直线对应的函数关系式为y=25x﹣75.
设线段DE所在直线对应的函数关系式为y=k2x+b2.
∵乙队按停工前的工作效率为:50÷(5﹣3)=25,
∴乙队剩下的需要的时间为:(160﹣50)÷25=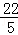 ,
,
∴E(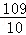 ,160),
,160),
∴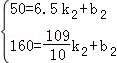 ,
,
解得: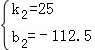
∴线段DE所在直线对应的函数关系式为y=25x﹣112.5.
(2)由题意,得
甲队每小时清理路面的长为 100÷5=20,
甲队清理完路面的时间,x=160÷20=8.
把x=8代入y=25x﹣112.5,得y=25×8﹣112.5=87.5.
答:当甲队清理完路面时,乙队铺设完的路面长为87.5米.
点评: 本题考查了待定系数法求一次函数的解析式的运用,工作总量=工作效率×工作时间的运用,解答时求出函数的解析式是关键.
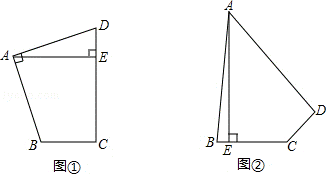
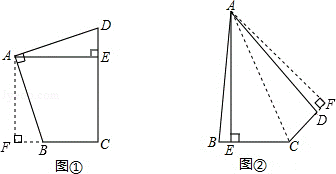
22.(9分)(2013•长春)探究:如图①,在四边形ABCD中,∠BAD=∠BCD=90°,AB=AD,AE⊥CD于点E.若AE=10,求四边形ABCD的面积.
应用:如图②,在四边形ABCD中,∠ABC+∠ADC=180°,AB=AD,AE⊥BC于点E.若AE=19,BC=10,CD=6,则四边形ABCD的面积为 152 .
考点: 全等三角形的判定与性质;正方形的判定与性质.
分析: 探究:过点A作AF⊥CB,交CB的延长线于点F,先判定四边形AFCE为矩形,根据矩形的四个角都是直角可得∠FAE=90°,然后利用同角的余角相等求出∠FAB=∠EAD,再利用“角角边”证明△AFB和△AED全等,根据全等三角形对应边相等可得AE=AF,从而得到四边形AFCE是正方形,然后根据正方形的面积公式列计算即可得解;
应用:过点A作AF⊥CD交CD的延长线于F,连接AC,根据同角的补角相等可得∠ABC=∠ADF,然后利用“角角边”证明△ABE和△ADF全等,根据全等三角形对应边相等可得AF=AE,再根据S四边形ABCD=S△ABC+S△ACD列式计算即可得解.
解答: 探究:如图①,过点A作AF⊥CB,交CB的延长线于点F,
∵AE⊥CD,∠BCD=90°,
∴四边形AFCE为矩形,
∴∠FAE=90°,
∴∠FAB+∠BAE=90°,
∵∠EAD+∠BAE=90°,
∴∠FAB=∠EAD,
∵在△AFB和△AED中,
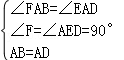 ,
,
∴△AFB≌△AED(AAS),
∴AF=AE,
∴四边形AFCE为正方形,
∴S四边形ABCD=S正方形AFCE=AE2=102=100;
应用:如图,过点A作AF⊥CD交CD的延长线于F,连接AC,
则∠ADF+∠ADC=180°,
∵∠ABC+∠ADC=180°,
∴∠ABC=∠ADF,
∵在△ABE和△ADF中,
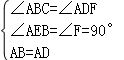 ,
,
∴△ABE≌△ADF(AAS),
∴AF=AE=19,
∴S四边形ABCD=S△ABC+S△ACD
=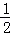 BC•AE+
BC•AE+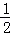 CD•AF
CD•AF
=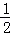 ×10×19+
×10×19+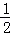 ×6×19
×6×19
=95+57
=152.
故答案为:152.
点评: 本题考查了全等三角形的判定与性质,正方形的判定与性质,(1)作辅助线构造出全等三角形是解题的关键;(2)作辅助线构造出全等三角形并把四边形分成两个三角形是解题的关键.
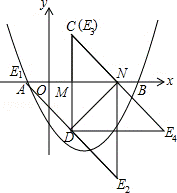
23.(10分)(2013•长春)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣2 与x轴交于点A(﹣1,0)、B(4,0).点M、N在x轴上,点N在点M右侧,MN=2.以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°.设点M的横坐标为m.
(1)求这条抛物线所对应的函数关系式.
(2)求点C在这条抛物线上时m的值.
(3)将线段CN绕点N逆时针旋转90°后,得到对应线段DN.
①当点D在这条抛物线的对称轴上时,求点D的坐标.
②以DN为直角边作等腰直角三角形DNE,当点E在这条抛物线的对称轴上时,直接写出所有符合条件的m值.
(参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标为(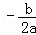 ,
,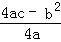 ))
))
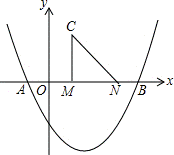
考点: 二次函数综合题
分析: (1)将A(﹣1,0)、B(4,0)两点的坐标代入y=ax2+bx﹣2,运用待定系数法即可求出抛物线的解析式;
(2)先根据等腰直角三角形的性质求出点C的坐标为(m,2),再将C的坐标代入y=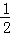 x2﹣
x2﹣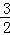 x﹣2,即可求出m的值;
x﹣2,即可求出m的值;
(3)①先由旋转的性质得出点D的坐标为(m,﹣2),再根据二次函数的性质求出抛物线y=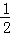 x2﹣
x2﹣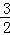 x﹣2的对称轴为直线x=
x﹣2的对称轴为直线x=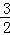 ,然后根据点D在直线x=
,然后根据点D在直线x=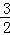 上,即可求出点D的坐标;
上,即可求出点D的坐标;
②以DN为直角边作等腰直角三角形DNE时,分别以D、N为直角顶点,在DN的两侧分别作出等腰直角三角形DNE,E点的位置分四种情况讨论.针对每一种情况,都可以先根据等腰直角三角形的性质求出点E的坐标,然后根据点E在直线x=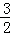 上,列出关于m的方程,解方程即可求出m的值.
上,列出关于m的方程,解方程即可求出m的值.
解答: 解:(1)∵抛物线经过点A(﹣1,0)、B(4,0),
∴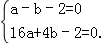
解得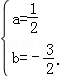
∴抛物线所对应的函数关系式为y=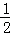 x2﹣
x2﹣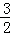 x﹣2;
x﹣2;
(2)∵△CMN是等腰直角三角形CMN,∠CMN=90°,
∴CM=MN=2,
∴点C的坐标为(m,2),
∵点C(m,2)在抛物线上,
∴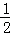 m2﹣
m2﹣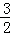 m﹣2=2,
m﹣2=2,
解得m1=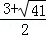 ,m2=
,m2=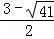 .
.
∴点C在这条抛物线上时,m的值为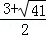 或
或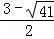 ;
;
(3)①∵将线段CN绕点N逆时针旋转90°后,得到对应线段DN,
∴∠CND=90°,DN=CN=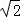 CM=
CM=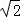 MN,
MN,
∴CD=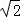 CN=2CM=2MN,
CN=2CM=2MN,
∴DM=CM=MN,∠DMN=90°,
∴点D的坐标为(m,﹣2).
又∵抛物线y=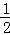 x2﹣
x2﹣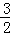 x﹣2的对称轴为直线x=
x﹣2的对称轴为直线x=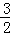 ,点D在这条抛物线的对称轴上,
,点D在这条抛物线的对称轴上,
∴点D的坐标为(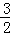 ,﹣2);
,﹣2);
②如图,以DN为直角边作等腰直角三角形DNE,E点的位置有四种情况:
如果E点在E1的位置时,
∵点D的坐标为(m,﹣2),MN=ME1=2,点N的坐标为(m+2,0),
∴点E1的(m﹣2,0),
∵点E1在抛物线y=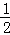 x2﹣
x2﹣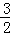 x﹣2的对称轴x=
x﹣2的对称轴x=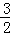 上,
上,
∴m﹣2=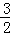 ,解得m=
,解得m=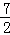 ;
;
如果E点在E2的位置时,
∵点D的坐标为(m,﹣2),点N的坐标为(m+2,0),
∴点E2的(m+2,﹣4),
∵点E2在抛物线y=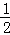 x2﹣
x2﹣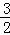 x﹣2的对称轴x=
x﹣2的对称轴x=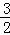 上,
上,
∴m+2=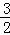 ,解得m=﹣
,解得m=﹣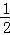 ;
;
如果E点在E3的位置时,
∵点D的坐标为(m,﹣2),
∴点E3的(m,2),
∵点E3在抛物线y=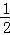 x2﹣
x2﹣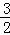 x﹣2的对称轴x=
x﹣2的对称轴x=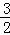 上,
上,
∴m=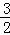 ;
;
如果E点在E4的位置时,
∵点D的坐标为(m,﹣2),点N的坐标为(m+2,0),
∴点E4的(m+4,﹣2),
∵点E4在抛物线y=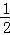 x2﹣
x2﹣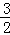 x﹣2的对称轴x=
x﹣2的对称轴x=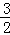 上,
上,
∴m+4=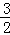 ,解得m=﹣
,解得m=﹣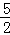 ;
;
综上可知,当点E在这条抛物线的对称轴上时,所有符合条件的m的值为m=﹣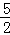 或m=﹣
或m=﹣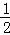 或m=
或m=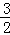 或m=
或m=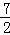 .
.
点评: 本题是二次函数的综合题型,其中涉及到运用待定系数法求抛物线的解析式,二次函数的性质,等腰直角三角形的性质,旋转的性质等知识,综合性较强,难度适中.其中(3)②要注意分析题意分情况讨论E点可能的位置,这是解题的关键.
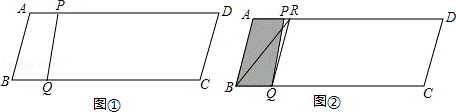
24.(12分)(2013•长春)如图①,在▱ABCD中,AB=13,BC=50,BC边上的高为12.点P从点B出发,沿B﹣A﹣D﹣A运动,沿B﹣A运动时的速度为每秒13个单位长度,沿A﹣D﹣A运动时的速度为每秒8个单位长度.点Q从点 B出发沿BC方向运动,速度为每秒5个单位长度.P、Q两点同时出发,当点Q到达点C时,P、Q两点同时停止运动.设点P的运动时间为t(秒).连结PQ.
(1)当点P沿A﹣D﹣A运动时,求AP的长(用含t的代数式表示).
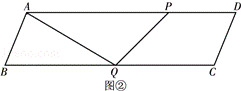
(2)连结AQ,在点P沿B﹣A﹣D运动过程中,当点P与点B、点A不重合时,记△APQ的面积为S.求S与t之间的函数关系式.
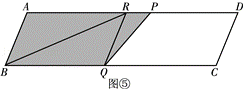
(3)过点Q作QR∥AB,交AD于点R,连结BR,如图②.在点P沿B﹣A﹣D运动过程中,当线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分时t的值.
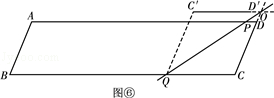
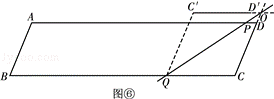
(4)设点C、D关于直线PQ的对称点分别为C′、D′,直接写出C′D′∥BC时t的值.
考点: 四边形综合题.
分析: (1)分情况讨论,当点P沿A﹣D运动时,当点P沿D﹣A运动时分别可以表示出AP的值;
(2)分类讨论,当0<t<1时,当1<t<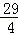 时,根据三角形的面积公式分别求出S与t的函数关系式;
时,根据三角形的面积公式分别求出S与t的函数关系式;
(3)分情况讨论,当0<t<1时,当1<t<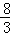 时,当
时,当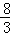 <t<
<t<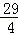 时,利用三角形的面积相等建立方程求出其解即可;
时,利用三角形的面积相等建立方程求出其解即可;
(4)分情况讨论当P在A﹣D之间或D﹣A之间时,如图⑥,根据轴对称的性质可以知道四边形QCOC′为菱形,根据其性质建立方程求出其解,当P在D﹣A之间如图⑦,根据菱形的性质建立方程求出其解即可.
解答: 解:(1)当点P沿A﹣D运动时,AP=8(t﹣1)=8t﹣8.
当点P沿D﹣A运动时,AP=50×2﹣8(t﹣1)=108﹣8t.(2分)
(2)当点P与点A重合时,BP=AB,t=1.
当点P与点D重合时,AP=AD,8t﹣8=50,t=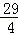 .
.
当0<t<1时,如图①.
作过点Q作QE⊥AB于点E.
S△ABQ=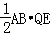 =
=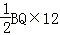 ,
,
∴QE=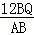 =
=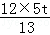 =
=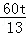 .
.
∴S=﹣30t2+30t.
当1<t≤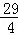 时,如图②.
时,如图②.
S=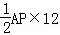 =
=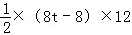 ,
,
∴S=48t﹣48;
(3)当点P与点R重合时,
AP=BQ,8t﹣8=5t,t=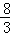 .
.
当0<t≤1时,如图③.
∵S△BPM=S△BQM,
∴PM=QM.
∵AB∥QR,
∴∠PBM=∠QRM,∠BPM=∠MQR,
在△BPM和△RQM中
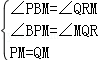 ,
,
∴△BPM≌△RQM.
∴BP=RQ,
∵RQ=AB,
∴BP=AB
∴13t=13,
解得:t=1
当1<t≤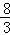 时,如图④.
时,如图④.
∵BR平分阴影部分面积,
∴P与点R重合.
∴t=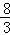 .
.
当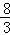 <t≤
<t≤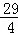 时,如图⑤.
时,如图⑤.
∵S△ABR=S△QBR,
∴S△ABR<S四边形BQPR.
∴BR不能把四边形ABQP分成面积相等的两部分.
综上所述,当t=1或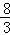 时,线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分.
时,线段PQ扫过的图形(阴影部分)被线段BR分成面积相等的两部分.
(4)如图⑥,当P在A﹣D之间或D﹣A之间时,C′D′在BC上方且C′D′∥BC时,
∴∠C′OQ=∠OQC.
∵△C′OQ≌△COQ,
∴∠C′OQ=∠COQ,
∴∠CQO=∠COQ,
∴QC=OC,
∴50﹣5t=50﹣8(t﹣1)+13,或50﹣5t=8(t﹣1)﹣50+13,
解得:t=7或t=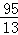 .
.
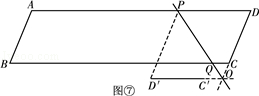
当P在A﹣D之间或D﹣A之间,C′D′在BC下方且C′D′∥BC时,如图⑦.
同理由菱形的性质可以得出:OD=PD,
∴50﹣5t+13=8(t﹣1)﹣50,
解得:t=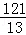 .
.
∴当t=7,t=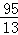 ,t=
,t=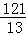 时,点C、D关于直线PQ的对称点分别为C′、D′,且C′D′∥BC.
时,点C、D关于直线PQ的对称点分别为C′、D′,且C′D′∥BC.



点评: 本题考查了平行四边形的性质的运用,菱形的性质的运用,全等三角形的判定及性质的运用,分类讨论的数学思想的运用,轴对称的性质的运用,三角形的面积公式的运用,解答时灵活运用动点问题的解答方法确定分界点是解答本题的关键和难点.


