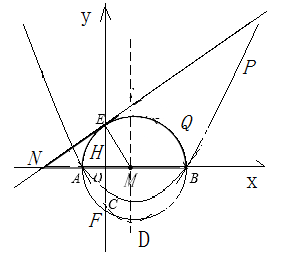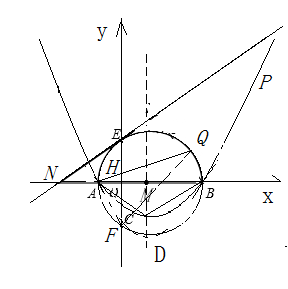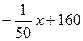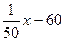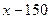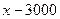(单词翻译:单击)
第Ⅰ卷(选择题40分)
一、选择题:本大题共12小题,其中1-8题每小题3分,9-12题每小题4分,满分40分.在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的字母代号填涂在答题卡相应位置上.
1.计算-22+3的结果是
A.7 B.5 C.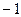 D.
D.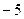
答案:C
解析:原式=-4+3=-1,选C。
2.下面所给的交通标志图中是轴对称图形的是
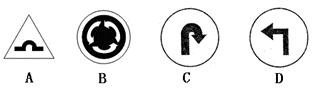
答案:A
解析:A中,等边三角形底边的中算线为对称轴,是轴对称图形,其它都不是轴对称图形。
3.如图,H7N9病毒直径为30纳米(1纳米=10-9米),用科学计数法表示这个病毒直径的大小,正确的是

A.30×10-9米 B. 3.0×10-8米
C. 3.0×10-10米 D. 0.3×10-9米
答案:B
解析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.
30纳米=30×10-9=3.0×10-8米
4.下列计算正确的是
A.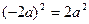
 B.
B.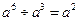 C.
C.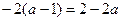 D.
D.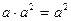
答案:C
解析:因为.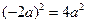 ,
,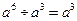 ,
,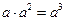 ,故A、B、D都错,只有C正确。
,故A、B、D都错,只有C正确。
5. 下图是某学校全体教职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在36≤x<38小组,而不在34≤x<36小组),根据图形提供的信息,下列说法中错误的是( )
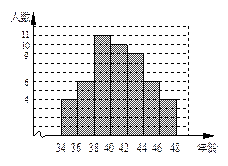
A.该学校教职工总人数是50人
B.年龄在40≤x<42小组的教职工人数占该学校总人数的20%
C.教职工年龄的中位数一定落在40≤x<42这一组
D.教职工年龄的众数一定在38≤x<40这一组
答案:D
解析:职工总人数为:4+6+11+10+9+6+4=50,故A正确;年龄在40≤x<42小组的教职工有10人,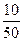 =0.2=20%,故B也正确,在38≤x<40这一组有11人,最多,因此,众数肯定在这组,D正确;中位数为6,故C错,选C。
=0.2=20%,故B也正确,在38≤x<40这一组有11人,最多,因此,众数肯定在这组,D正确;中位数为6,故C错,选C。
6.如果点P(2x+6,x-4)在平面直角坐标系的第四象限内,那么x的取值范围在数轴上可表示为( )
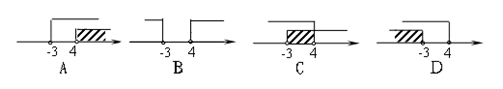
答案:C
解析:因为点P在第四象限,所以,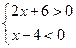 ,即
,即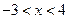 ,所以,选C。
,所以,选C。
7.四个命题: ①三角形的一条中线能将三角形分成面积相等的两部分; ②有两边和其中一边的对角对应相等的两个三角形全等; ③点P(1,2)关于原点的对称点坐标为(-1,-2); ④两圆的半径分别是3和4,圆心距为d,若两圆有公共点,则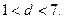 其中正确的是
其中正确的是
A. ①② B.①③ C.②③ D.③④
答案:B
解析:三角形的中线分成两个三角形底边相等,高相同,故面积相等,①正确;两边和两边夹角对应相等的两个三角形才全等,故②错误;③正确;当d=1或d=7时,两圆有一个公共点,故④不正确,选B。
8.已知一元二次方程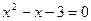 的较小根为
的较小根为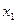 ,则下面对
,则下面对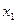 的估计正确的是
的估计正确的是
A.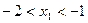 B.
B.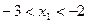
C.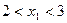 D.
D.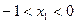
答案:A
解析:用求根公式,得: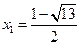 ,
,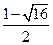 <
<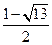 <
<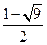 ,即
,即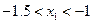 ,只有A是正确的。
,只有A是正确的。
9. 甲计划用若干个工作日完成某项工作,从第三个工作日起,乙加入此项工作,且甲、乙两人工效相同,结果提前3天完成任务,则甲计划完成此项工作的天数是
A.8 B.7 C.6 D.5
答案:A
解析:假设每天工作量是1,甲单独工作x天完成。工作总量等于1×x,实际工作中甲做的1×(x-3);乙做的1×(x-2-3)
1×x=1×(x-3)+1×(x-2-3),解得:x=8
10. 如图,在△ABC中,以BC为直径的圆分别交边AC、AB于D、E两点,连接BD、DE.若BD平分∠ABC,则下列结论不一定成立的是
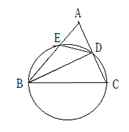
A.BD⊥AC B.AC2=2AB·AE
C.△ADE是等腰三角形 D. BC=2AD.
答案:D
解析:因为BC为直线,所以,A正确;可证△BCD≌△BAD,得BC=BA,AD=CD,
又△ADE∽△ABC,可得:AD••••••••••••AC=ADE•AB,而AC=2AD,可知B正确;因为ADE∽△ABC,
△ABC是等腰三角形,所以,△ADE是等腰三角形,C也正确;只有D不一定成立。
11.如图,下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M与m、n的关系是
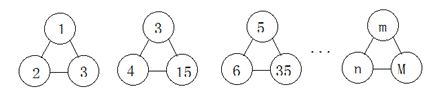
A. M=mn B. M=n(m+1) C.M=mn+1 D.M=m(n+1)
答案:D
解析:因为3=(2+1)×1,,15=(4+1)×3,35=(6+1)×5,所以,M=(n+1)×m,选D。
12.如图,已知抛物线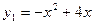 和直线
和直线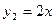 .我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M= y1=y2.
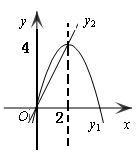
下列判断: ①当x>2时,M=y2;
②当x<0时,x值越大,M值越大;
③使得M大于4的x值不存在;
④若M=2,则x= 1 .其中正确的有
A.1个 B.2个 C. 3个 D.4个
答案:B
解析:当x>2时,由图象可知y2>y1,M=y1,所以,①不正确;当x<0时,由图象可知y2>y1,M=y1,x值越大,M值越大,②正确;M最大值为4,所以,③正确;M=2时,x的值有两个,不一定是1,所以,④不正确,正确的有2个,选B。
第Ⅱ卷(非选择题80分)
二、填空题:本大题共4小题,每小题4分,满分16分.不需写出解答过程,请将答案直接写在答题卡相应位置上.
13.要使式子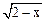 有意义,则
有意义,则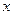 的取值范围是 .
的取值范围是 .
答案:x≤2
解析:由根式的意义,得:2-x≥0,解得:x≤2
14.已知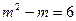 ,则
,则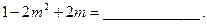
答案:-11
解析:原式=1-2(m2-m)-1-12=-11
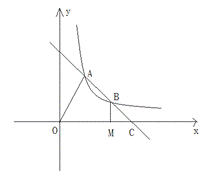
15. 如右图,直线AB交双曲线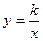 于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,S⊿OAC=12,则k的值为___________.
于A、B,交x轴于点C,B为线段AC的中点,过点B作BM⊥x轴于M,连结OA.若OM=2MC,S⊿OAC=12,则k的值为___________.
答案:8
解析:过A作AN⊥OC于N,因为BM⊥x轴,所以,AN∥BM,因为B为AC中点,所以MN=MC,
又OM=2MC=2MN,所以,N为OM中点,设A(a,b),
则OC=3a,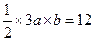 ,得ab=8,又点A在双曲线上,所以,k=ab=8。
,得ab=8,又点A在双曲线上,所以,k=ab=8。
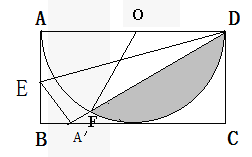
16.如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为_____________.
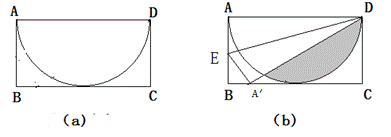
答案: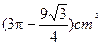
解析:半圆的半径为3,所以,AB=CD=3,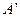 D=AD=6,
D=AD=6,
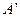 C=3
C=3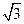 ,
,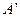 B=6-3
B=6-3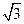 ,设AE=x,在直角三角形EB
,设AE=x,在直角三角形EB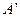 中,
中,
(3-x)2+(6-3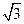 )2=x2,解得:x=12-6
)2=x2,解得:x=12-6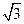 ,tan∠ADE=
,tan∠ADE=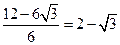 ,所以,∠ADE=15°,∠ADF=30°,∠AOF=60°,
,所以,∠ADE=15°,∠ADF=30°,∠AOF=60°,
S半圆AD=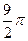 ,S扇形AOF=
,S扇形AOF=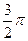 ,
,
S△DOF=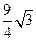 ,
,
所以,阴影部分面积为: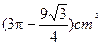
三、解答题:本大题有6小题,满分64分.请在答题卡指定区域内作答,解答时应写出必要的文字说明、证明过程或演算步骤.
17.(本题满分10分,(1)小题4分,(2)小题6分)
(1)计算: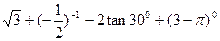
(2)已知,关于x的方程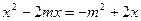 的两个实数根
的两个实数根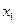 、
、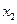 满足
满足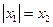 ,求实数
,求实数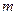 的值.
的值.
解析: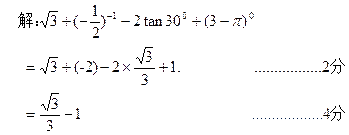
(2)(本小题满分6分)
解:原方程可变形为: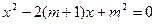 . …………………5分
. …………………5分
∵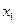 、
、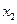 是方程的两个根,
是方程的两个根,
∴△≥0,即:4(m +1)2-4m2≥0, ∴ 8m+4≥0, m≥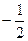 .
.
又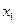 、
、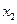 满足
满足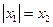 ,∴
,∴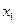 =
=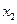 或
或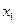 =-
=-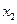 , 即△=0或
, 即△=0或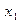 +
+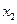 =0, …………………8分
=0, …………………8分
由△=0,即8m+4=0,得m=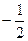 .
.
由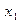 +
+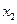 =0,即:2(m+1)=0,得m=-1,(不合题意,舍去)
=0,即:2(m+1)=0,得m=-1,(不合题意,舍去)
所以,当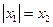 时,m的值为
时,m的值为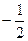 . ……………10分
. ……………10分
18.(本题满分10分)
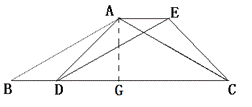
如图,已知四边形ABDE是平行四边形,C为边B D延长线上一点,连结AC、CE,使AB=AC.
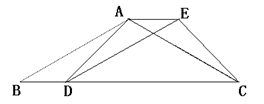
⑴求证:△BAD≌△AEC;
⑵若∠B=30°,∠ADC=45°,BD=10,求平行四边形ABDE的面积.
解析:
(1)证明:∵AB=AC,∴∠B=∠ACB.
又 ∵四边形ABDE是平行四边形
∴AE∥BD, AE=BD,∴∠ACB=∠CAE=∠B,
∴⊿DBA≌⊿AEC(SAS) ………………4分
(2)过A作AG⊥BC,垂足为G.设AG=x,
在Rt△AGD中,∵∠ADC=450,∴AG=DG=x,
在Rt△AGB中,∵∠B=300,∴BG=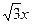 ,………………6分
,………………6分
又∵BD=10.
∴BG-DG=BD,即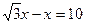 ,解得AG=x=
,解得AG=x=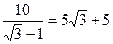 .…………………8分
.…………………8分
∴S平行四边形ABDE=BD·AG=10×(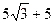 )=
)=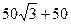 .………………10分
.………………10分
19.(本题满分10分)
“端午”节前,小明爸爸去超市购买了大小、形状、重量等都相同的火腿粽子和豆沙粽子若干,放入不透明的盒中,此时从盒中随机取出火腿粽子的概率为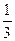 ;妈妈从盒中取出火腿粽子3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出火腿粽子的概率为
;妈妈从盒中取出火腿粽子3只、豆沙粽子7只送给爷爷和奶奶后,这时随机取出火腿粽子的概率为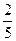 .
.
(1)请你用所学知识计算:爸爸买的火腿粽子和豆沙粽子各有多少只?
(2)若小明一次从盒内剩余粽子中任取2只,问恰有火腿粽子、豆沙粽子各1只的概率是多少?(用列表法或树状图计算)
解析:(1)设爸爸买的火腿粽子和豆沙粽子分别为x只、y只, ……1分
根据题意得: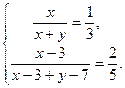 …………………………………4分
…………………………………4分
解得: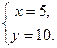 经检验符合题意,
经检验符合题意,
所以爸爸买了火腿粽子5只、豆沙粽子10只. ……………6分
(2)由题可知,盒中剩余的火腿粽子和豆沙粽子分别为2只、3只,我们不妨把两只火腿粽子记为a1、a2;3只豆沙粽子记为b1、b2、b3,则可列出表格如下:
a1 | a2 | b1 | b2 | b3 | |
a1 | a1 a2 | a1b1 | a1b2 | a1b3 | |
a2 | a2 a1 | a2 b1 | a2 b2 | a2 b3 | |
b1 | b1 a1 | b1a2 | b1 b2 | b1 b3 | |
b2 | b2 a1 | b2a2 | b2b1 | b2 b3 | |
b3 | b3 a1 | b3a2 | b3b1 | b3b2 |
…………8分
∴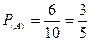 …………………10分
…………………10分
20. (本题满分10分)
问题背景:
如图(a),点A、B在直线l的同侧,要在直线l上找一点C,使AC与BC的距离之和最小,我们可以作出点B关于l的对称点B′,连接A B′与直线l交于点C,则点C即为所求.
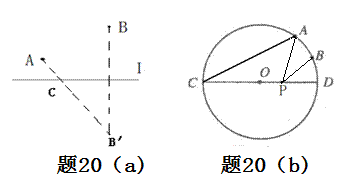
(1)实践运用:
如图(b),已知,⊙O的直径CD为4,点A 在⊙O 上,∠ACD=30°,B 为弧AD 的中点,P为直径CD上一动点,则BP+AP的最小值为__________.
(2)知识拓展:
如图(c),在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E、F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.
解析: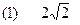 …………………4分
…………………4分
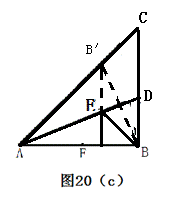
(2)解:如图,在斜边AC上截取AB′=AB,连结BB′.
∵AD平分∠BAC,
∴点B与点B′关于直线AD对称. …………6分
过点B′作B′F⊥AB,垂足为F,交AD于E,连结BE,
则线段B′F的长即为所求.(点到直线的距离最短) ………8分
在Rt△AFB/中,∵∠BAC=450, AB/=AB= 10,
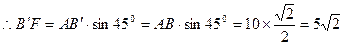 ,
,
∴BE+EF的最小值为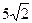 . ………………10分
. ………………10分
21. (本小题满分10分)
一汽车租赁公司拥有某种型号的汽车100辆.公司在经营中发现每辆车的月租金x(元)与每月租出的车辆数(y)有如下关系:
x | 3000 | 3200 | 3500 | 4000 |
y | 100 | 96 | 90 | 80 |
(1)观察表格,用所学过的一次函数、反比例函数或二次函数的有关知识求出每月租出的车辆数y(辆)与每辆车的月租金x(元)之间的关系式.
(2)已知租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.用含x(x≥3000)的代数式填表:
租出的车辆数 | 未租出的车辆数 | ||
租出每辆车的月收益 | 所有未租出的车辆每月的维护费 |
(3)若你是该公司的经理,你会将每辆车的月租金定为多少元,才能使公司获得最大月收益?请求出公司的最大月收益是多少元.
解析:(1)由表格数据可知y与x是一次函数关系,设其解析式ONG为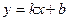 .
.
由题: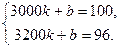 解之得:
解之得: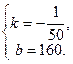
∴y与x间的函数关系是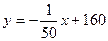 . ……………………………3分
. ……………………………3分
(2)如下表:每空1分,共4分.
租出的车辆数 |
| 未租出的车辆数 |
|
租出的车每辆的月收益 |
| 所有未租出的车辆每月的维护费 |
|
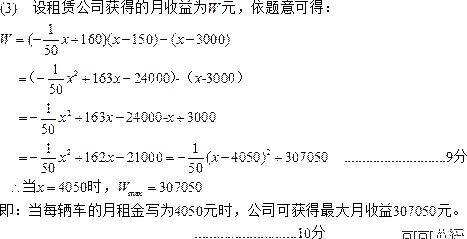
22. (本小题满分14分)
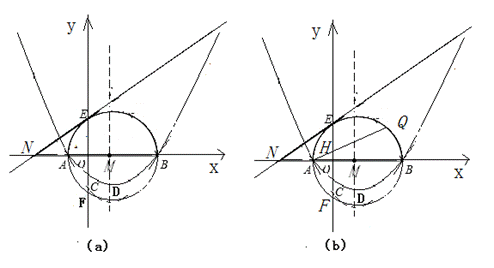
已知,如图(a),抛物线y=ax2+bx+c经过点A(x1,0),B(x2,0),C(0,-2),其顶点为D.以AB为直径的⊙M交y轴于点E、F,过点E作⊙M的切线交x轴于点N.∠ONE=30°,|x1-x2|=8.
(1)求抛物线的解析式及顶点D的坐标;
(2)连结AD、BD,在(1)中的抛物线上是否存在一点P,使得⊿ABP与⊿ADB相似?若存在,求出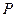 点的坐标;若不存在,说明理由;
点的坐标;若不存在,说明理由;
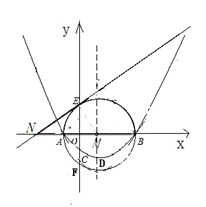
(3)如图(b),点Q为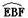 上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:
上的动点(Q不与E、F重合),连结AQ交y轴于点H,问:
AH·AQ是否为定值?若是,请求出这个定值;若不是,请说明理由.
解析:

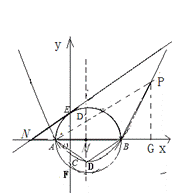
(2)如图,由抛物线的对称性可知:
 ,
,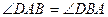 .
.
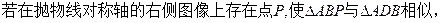
必须有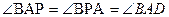 .
.
设AP交抛物线的对称轴于D′点,
显然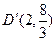 ,
,
∴直线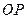 的解析式为
的解析式为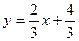 ,
,
由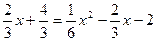 ,得
,得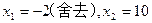 .
.
∴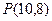 .
.
过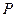 作
作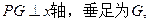
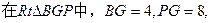
∵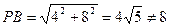
∴ ..
..
∴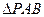 与
与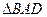 不相似, …………………………9分
不相似, …………………………9分
同理可说明在对称轴左边的抛物线上也不存在符合条件的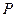 点.
点.
所以在该抛物线上不存在点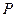 ,使得与
,使得与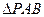 与相似.…………………… 10分
与相似.…………………… 10分
(3)连结AF、QF,
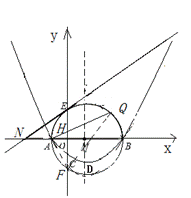
在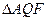 和
和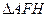 中,
中,
由垂径定理易知:弧AE=弧AF.
∴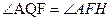 ,
,
又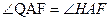 ,
,
∴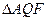 ∽
∽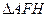 ,
,
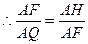 ,
,
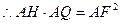 ……………… 12分
……………… 12分
在Rt△AOF中,AF2=AO2+OF2=22+(2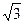 )2=16(或利用AF2=AO·AB=2×8=16)
)2=16(或利用AF2=AO·AB=2×8=16)
∴AH·AQ=16
即:AH·AQ为定值。 …………… 14分