(单词翻译:单击)
一、选择题(共10小题,每小题3分,满分30分)
1.(3分)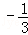 的绝对值是( )
的绝对值是( )
A. 3 B. ﹣3 C. 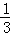 D.
D. 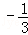
2.(3分)如图放置的圆柱体的左视图为( )
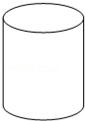
A. |
| B. |
| C. |
| D. |
|
3.(3分)下列运算正确的是( )
A. a3•a2=a6 B. 2a(3a﹣1)=6a3﹣1 C. (3a2)2=6a4 D. 2a+3a=5a
4.(3分)如图,直线AB∥CD,直线EF与AB, CD分别交于点E,F,EC⊥EF,垂足为E,若∠1=60°,则∠2的度数为( )
CD分别交于点E,F,EC⊥EF,垂足为E,若∠1=60°,则∠2的度数为( )
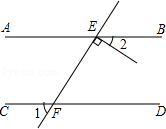
A. 15° B. 30° C. 45° D. 60°
5.(3分)下列说法中,正确的是( )
A. 对载人航天器“神舟十号”的零部件的检查适合采用抽样调查的方式
B. 某市天气预报中说“明天降雨的概率是80%”,表示明天该市有80%的地区降雨
C. 第一枚硬币,正面朝上的概率为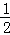
D. 若甲组数据的方差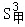 =0.1,乙组数据的方差
=0.1,乙组数据的方差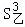 =0.01,则甲组数据比乙组数据稳定
=0.01,则甲组数据比乙组数据稳定
6.(3分)甲、乙两盒中各放入分别写有数字1,2,3的三张卡片,每张卡片除数字外其他完全相同.从甲盒中随机抽出一张卡片,再从乙盒中随机摸出一张卡片,摸出的两张卡片上的数字之和是3的概率是( )
A. 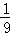 B.
B. 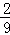 C.
C. 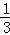 D.
D. 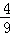
7.(3分)如图,在菱形ABCD中,∠BAD=2∠B,E,F分别为BC,CD的中点,连接AE、AC、AF,则图中与△ABE全等的三角形(△ABE除外)有( )
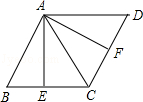
A. 1个 B. 2个 C. 3个 D. 4个
8.(3分)某服装加工厂计划加工400套运动服,在加工完160套后,采用了新技术,工作效率比原计划提高了20%,结果共有了18天完成全部任务.设原计划每天加工x套运动服,根据题意可列方程为( )
A. 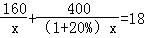 B.
B. 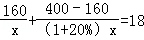
C. 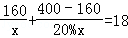 D.
D. 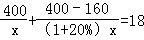
9.(3分)如图,⊙O的半径是3,点P是弦AB延长线上的一点,连接OP,若OP=4,∠APO=30°,则弦AB的长为( )
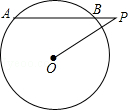
A. 2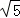 B.
B. 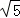 C. 2
C. 2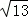 D.
D. 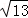
10.(3分)如图,在矩形OABC中,AB=2BC,点A在y轴的正半轴上,点C在x轴的正半轴上,连接OB,反比例函数y=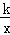 (k≠0,x>0)的图象经过OB的中点D,与BC边交于点E,点E的横坐标是4,则k的值是( )
(k≠0,x>0)的图象经过OB的中点D,与BC边交于点E,点E的横坐标是4,则k的值是( )
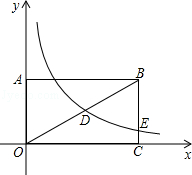
A. 1  B. 2 C. 3 D. 4
B. 2 C. 3 D. 4
二、填空题(共8小题,每小题3分,满分24分)
11.(3分)在函数y=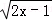 中,自变量x的取值范围是___________.
中,自变量x的取值范围是___________.
12.(3分)一种花粉颗粒的直径约为0.0000065米,将0.0000065用科学记数法表示为___________.
13.(3分)在平面直角坐标系中,点P(5,﹣3)关于原点对称的点的坐标是___________.
14.(3分)在一个不透明的袋子里装有黄色、白色乒乓球共40个,除颜色外其他完全相同.小明从这个袋子中随机摸出一球,放回.通过多次摸球实验后发现,摸到黄色球的概率稳定在15%附近,则袋中黄色球可能有___________个.
15.(3分)在平面直角坐标系中,把抛物线y=﹣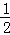 x2+
x2+ 1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是___________.
1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是___________.
16.(3分)已知圆锥底面圆的半径为6cm,它的侧面积为60πcm2,则这个圆锥的高是___________cm.
17.(3分)如图,在矩形ABCD中,AB=10,AD=4,点P是边AB上一点,若△APD与△BPC相似,则满足条件的点P有__________个.

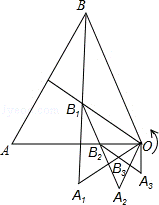
18.(3分)如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OBA的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是__________.
三、解答题(共2小题,共22分)
19.(10分)
(1)计算: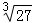 +(x﹣2)0﹣
+(x﹣2)0﹣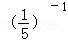 ﹣2cos45°
﹣2cos45°
(2)先化简,再求值:(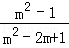 +
+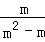 )+(1+
)+(1+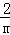 ),其中m=﹣3.
),其中m=﹣3.
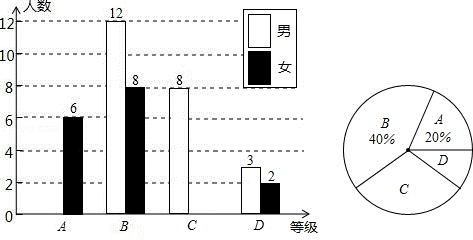
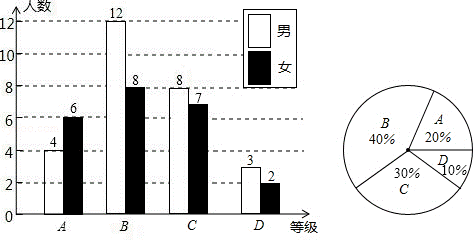
20.(12分)某校对九年级全体学生进行了一次学业水平测试,成绩评定分为A,B,C,D四个等级(A,B,C,D分别代表优秀、良好、合格、不合格)该校从九年级学生中随机抽取了一部分学生的成绩,绘制成以下不完整的统计图.请你根据统计图提供的信息解答下列问题;
(1)本次调查中,一共抽取了________名学生的成绩;
(2)将上面的条形统计图补充完整,写出扇形统计图中等级C的百分比________.
(3)若等级D的5名学生的成绩(单位:分)分别是55、48、57、51、55.则这5个数据的中位数是________分,众数是________分.
(4)如果该校九年级共有500名学生,试估计在这次测试中成绩达到优秀的人数.
四、解答题(共6小题,满分74分)
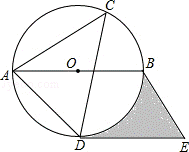
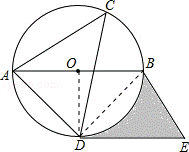
21.(12分)如图,⊙O是△ACD的外接圆,AB是直径,过点D作直线DE∥AB,过点B作直线BE∥AD,两直线交于点E,如果∠ACD=45°,⊙O的半径是4cm
(1)请判断DE与⊙O的位置关系,并说明理由;
(2)求图中阴影部分的面积(结果用π表示).
22.(12分)某中学响应“阳光体育”活动的号召,准备从体育用品商店购买一些排球、足球和篮球,排球和足球的单价相同,同一种球的单价相同,若购买2个足球和3个篮球共需340元,购买4个排球和5个篮球共需600元.
(1)求购买一个足球,一个篮球分别需要多少元?
(2)该中学根据实际情况,需从体育用品商店一次性购买三种球共100个,且购买三种球的总费用不超过600元,求这所中学最多可以购买多少个篮球?
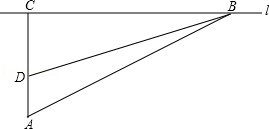
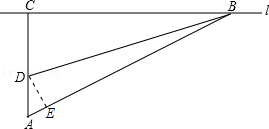
23.(12分)校车安全是近几年社会关注的热点问题,安全隐患主要是超速和超载.某中学九年级数学活动小组进行了测试汽车速度的实验,如图,先在笔直的公路l旁选取一点A,在公路l上确定点B、C,使得AC⊥l,∠BAC=60℃,再在AC上确定点D,使得∠BDC=75°,测得AD=40米,已知本路段对校车限速是50千米/时,若测得某校车从B到C匀速行驶用时10秒,问这辆车在本路段是否超速?请说明理由(参考数据: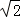 =1.41,
=1.41,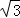 =1.73)
=1.73)
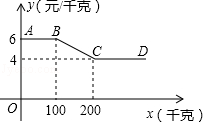
24.(12分)某蔬菜经销商到蔬菜种植基地采购一种蔬菜,经销商一次性采购蔬菜的采购单价y(元/千克)与采购量x(千克)之间的函数关系图象如图中折线AB﹣﹣BC﹣﹣CD所示(不包括端点A).
(1)当100<x<200时,直接写y与x之间的函数关系式: .
(2)蔬菜的种植成本为2元/千克,某经销商一次性采购蔬菜的采购量不超过200千克,当采购量是多少时,蔬菜种植基地获利最大,最大利润是多少元?
(3)在(2)的条件下,求经销商一次性采购的蔬菜是多少千克时,蔬菜种植基地能获得418元的利润?
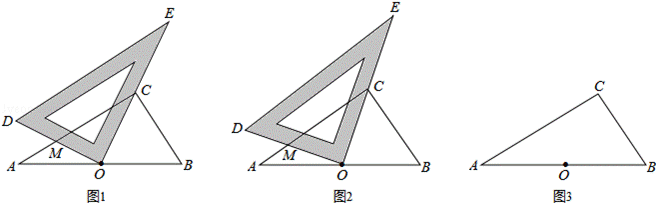
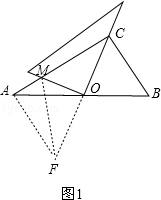
25.(12分)在△ABC中,∠ACB=90°,∠A<45°,点O为AB中点,一个足够大的三角板的直角顶点与点O重合,一边OE经过点C,另一边OD与AC交于点M.
(1)如图1,当∠A=30°时,求证:MC2=AM2+BC2;
(2)如图2,当∠A≠30°时,(1)中的结论是否成立?如果成立,请说明理由;如果不成立,请写出你认为正确的结论,并说明理由;
(3)将三角形ODE绕点O旋转,若直线OD与直线AC相交于点M,直线OE与直线BC相交于点N,连接MN,则MN2=AM2+BN2成立吗?
答: (填“成立”或“不成立”)
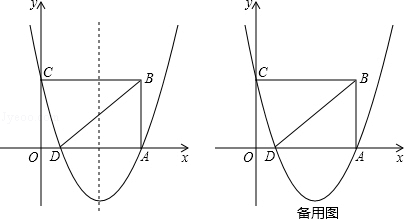
26.(14分)如图,在平面直角坐标系中,点O是原点,矩形OABC的顶点A在x轴的正半轴上,顶点C在y的正半轴上,点B的坐标是(5,3),抛物线y=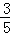 x2+bx+c经过A、C两点,与x轴的另一个交点是点D,连接BD.
x2+bx+c经过A、C两点,与x轴的另一个交点是点D,连接BD.
(1)求抛物线的解析式;
(2)点M是抛物线对称轴上的一点,以M、B、D为顶点的三角形的面积是6,求点M的坐标;
(3)点P从点D出发,以每秒1个单位长度的速度沿D→B匀速运动,同时点Q从点B出发,以每秒1个单位长度的速度沿B→A→D匀速运动,当点P到达点B时,P、Q同时停止运动,设运动的时间为t秒,当t为何值时,以D、P、Q为顶点的三角形是等腰三角形?请直接写出所有符合条件的值.
一、选择题(共10小题,每小题3分,满分30分)
1.C
2.A
3.D
4.B
5.C
6.B
7.C
8.B
9.A
10.B
二、填空题(共8小题,每小题3分,满分24分)
11. x≥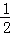
12. 6.5×10﹣6
13. (﹣5,3)
14. 6
15. y=﹣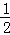 (x+1)2+4
(x+1)2+4
16. 8
17. 3
18. 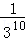
三、解答题(共2小题,共22分)
19.解:(1)原式=3+1﹣5+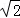 =
=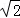 ﹣1;
﹣1;
(2)原式=[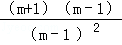 +
+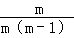 ]÷
]÷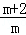
=(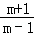 +
+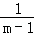 )÷
)÷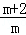
=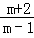 •
•
=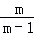 ,
,
当m=﹣3时,原式=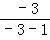 =
=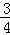 .
.
20.解:
(1)根据题意得:(12+8)÷40%=50(人),则本次调查了50名学生的成绩;
(2)等级A的学生数为50×20%=10(人),即等级A男生为4人;
∵等级D占的百分比为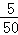 ×100%=10%;
×100%=10%;
∴等级C占的百分比为1﹣(40%+20%+10%)=30%,
∴等级C的学生数为50×30%=15(人),即女生为7人,
补全条形统计图,如图所示:
(3)根据题意得:500×20%=100(人),则在这次测试中成绩达到优秀的人数有100人.
四、解答题(共6小题,满分74分)
21.解:(1)DE与⊙O相切.理由如下:
连结OD,则∠ABD=∠ACD=45°,
∵AB是直径,
∴∠ADB=90°,
∴△ADB为等腰直角三角形,
而点O为AB的中点,
∴OD⊥AB,
∵DE∥AB,
∴OD⊥DE,
∴DE为⊙O的切线;
(2)∵BE∥AD,DE∥AB,
∴四边形ABED为平行四边形,
∴DE=AB=8cm,
∴S阴影部分=S梯形BODE﹣S扇形OBD
=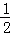 (4+8)×4﹣
(4+8)×4﹣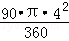
=(24﹣4π)cm2.
22.解:(1)设购买一个足球需要x元,则购买一个排球也需要x元,购买一个篮球y元,
由题意得: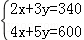 ,
,
解得: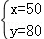 ,
,
答:购买一个足球需要50元,购买一个篮球需要80元;
(2)设该中学购买篮球m个,
由题意得:80m+50(100﹣m)≤600,
解得:m≤33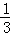 ,
,
∵m是整数,
∴m最大可取33.
答:这所中学最多可以购买篮球33个
23.解:过点D作DE⊥AB于点E,
∵∠CDB=75°,
∴∠CBD=15°,∠EBD=15°(外角的性质),
在Rt△CBD和Rt△EBD中,
∵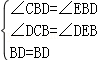 ,
,
∴△CBD≌△EBD,
∴CD=DE,
在Rt△ADE中,∠A=60°,AD=40米,
则DE=ADsin60°=20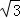 米,
米,
故AC=AD+CD=AD+DE=(40+20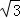 )米,
)米,
在Rt△ABC中,BC=ACtan∠A=(40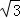 +60)米,
+60)米,
则速度=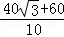 =4
=4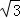 +6≈12.92米/秒,
+6≈12.92米/秒,
∵12.92米/秒=46.512千米/小时,
∴该车没有超速.
24.解;(1)设当100<x<200时,y与x之间的函数关系式为:y=ax+b,
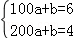 ,
,
解得: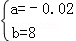
∴y与x之间的函数关系式为:y=﹣0.02x+8;
故答案为:y=﹣0.02x+8;
(2)当采购量是x千克时,蔬菜种植基地获利W元,
当0<x≤100时,W=(6﹣2)x=4x,
当x=100时,W有最大值400元,
当100<x≤200时,
W=(y﹣2)x
=(﹣0.02x+6)x
=﹣0.02(x﹣150)2+450,
∵当x=150时,W有最大值为450元,
综上所述,一次性采购量为150千克时,蔬菜种植基地能获得最大利润为450元;
(3)∵418<450,
∴根据(2)可得,﹣0.02(x﹣150)2+450=418
解得:x1=110,x 2=190,
答:经销商一次性采购的蔬菜是110千克或190千克时,蔬菜种植基地能获得418元的利润.
25. (1)证明:如图1,过A作AF⊥AC交CO延长线于F,连接MF,
∵∠ACB=90°,
∴BC∥AF,
∴△BOC∽△AOF,
∴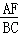 =
=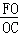 =
=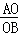 ,
,
∵O为AB中点,
∴OA=OB,
∴AF=BC,CO=OF,
∵∠MOC=90°,
∴OM是CF的垂直平分线,
∴CM=MF,
在Rt△AMF中,由勾股定理得:MF2=AM2+AF2=AM2+BC2,
即MC2=AM2+BC2;
(2)解:不成立,
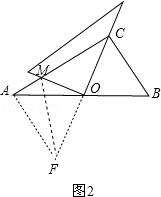
理由是:如图2,
过A作AF⊥AC交CO延长线于F,连接MF,
∵∠ACB=90°,
∴BC∥AF,
∴△BOC∽△AOF,
∴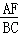 =
=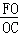 =
=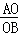 ,
,
∵OA=O B,
B,
∴AF=BC,CO=OF,
∵∠MOC=90°,
∴OM是CF的垂直平分线,
∴CM=MF,
在Rt△AMF中,由勾股定理得:MF2=AM2+AF2=AM2+BC2,
即MC2=AM2+BC2;
(3)成立.
26.解:(1)∵矩形ABCD,B(5,3),
∴A(5,0),C(0,3).
∵点A(5,0),C(0,3)在抛物线y=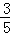 x2+bx+c上,
x2+bx+c上,
∴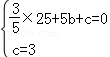 ,解得:b=
,解得:b=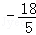 ,c=3.
,c=3.
∴抛物线的解析式为:y=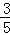 x2
x2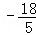 x+3.
x+3.
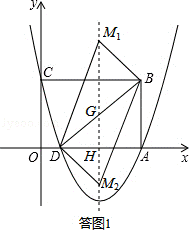
(2)如答图1所示,
∵y=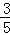 x2
x2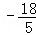 x+3=
x+3=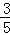 (x﹣3)2﹣
(x﹣3)2﹣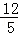 ,
,
∴抛物线的对称轴为直线x=3.
如答图1所示,设对称轴与BD交于点G,与x轴交于点H,则H(3,0).
令y=0,即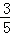 x2
x2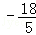 x+3=0,解得x=1或x=5.
x+3=0,解得x=1或x=5.
∴D(1,0),∴DH=2,AH=2,AD=4.
∵tan∠ADB=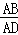 =
=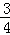 ,∴GH=DH•tan∠ADB=2×
,∴GH=DH•tan∠ADB=2×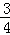 =
=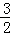 ,
,
∴G(3,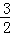 ).
).
∵S△MBD=6,即S△MDG+S△MBG=6,
∴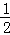 MG•DH+
MG•DH+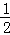 MG•AH=6,
MG•AH=6,
即: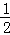 MG×2+
MG×2+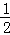 MG×2=6,
MG×2=6,
解得:MG=3.
∴点M的坐标为(3,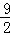 )或(3,
)或(3,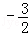 ).
).
(3)在Rt△ABD中,AB=3,AD=4,则BD=5,∴sinB=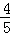 ,cosB=
,cosB=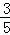 .
.
以D、P、Q为顶点的三角形是等腰三角形,则:
①若PD=PQ,如答图2所示:
此时有P D=PQ=BQ=t,过点Q作QE⊥BD于点E,
D=PQ=BQ=t,过点Q作QE⊥BD于点E,
则BE=PE,BE=BQ•cosB=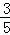 t,QE=BQ•sinB=
t,QE=BQ•sinB=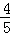 t,
t,
∴DE=t+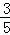 t=
t=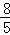 t.
t.
由勾股定理得:DQ2=DE2+QE2=AD2+AQ2,
即(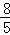 t)2+(
t)2+(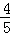 t)2=42+(3﹣t)2,
t)2=42+(3﹣t)2,
整理得:11t2+6t﹣25=0,
解得:t=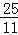 或t=﹣5(舍去),
或t=﹣5(舍去),
∴t=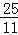 ;
;
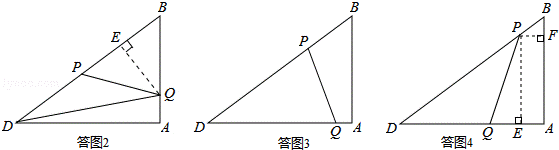
②若PD=DQ,如答图3所示:
此时PD=t,DQ=AB+AD﹣t=7﹣t,
∴t=7﹣t,
∴t=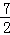 ;
;
③若PQ=DQ,如答图4所示:
∵PD=t,∴BP=5﹣t;
∵DQ=7﹣t,∴PQ=7﹣t,AQ=4﹣(7﹣t)=t﹣3.
过点P作PF⊥AB于点F,则PF=PB•sinB=(5﹣t)×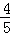 =4﹣
=4﹣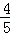 t,BF=PB•cosB=(5﹣t)×
t,BF=PB•cosB=(5﹣t)×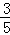 =3﹣
=3﹣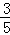 t.
t.
∴AF=AB﹣BF=3﹣(3﹣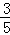 t)=
t)=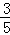 t.
t.
过点P作PE⊥AD于点E,则PEAF为矩形,
∴PE=AF=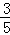 t,AE=PF=4﹣
t,AE=PF=4﹣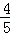 t,∴EQ=AQ﹣AE=(t﹣3)﹣(4﹣
t,∴EQ=AQ﹣AE=(t﹣3)﹣(4﹣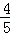 t)=
t)=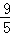 t﹣7.
t﹣7.
在Rt△PQE中,由勾股定理得:EQ2+PE2=PQ2,
即:(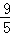 t﹣7)2+(
t﹣7)2+(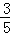 t)2=(7﹣t)2,
t)2=(7﹣t)2,
整理得:13t2﹣56t=0,
解得:t=0(舍去)或t=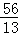 .
.
∴t=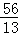 .
.
综上所述,当t=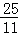 ,t=
,t=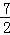 或t=
或t=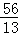 时,以D、P、Q为顶点的三角形是等腰三角形.
时,以D、P、Q为顶点的三角形是等腰三角形.






