(单词翻译:单击)
一.选择题:
1.下列等式成立的是A
A .│-2│=2 B.(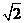 -1)0=0 C.(-
-1)0=0 C.(-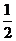 )
)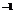 =2 D.-(-2)=-2
=2 D.-(-2)=-2
答案:A
解析:因为(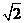 -1)0=1,(-
-1)0=1,(-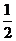 )
)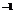 =-2,-(-2)=2,所以B、C、D都不正确,又负数的绝对值是它的相反数,故选A。
=-2,-(-2)=2,所以B、C、D都不正确,又负数的绝对值是它的相反数,故选A。
2.如图,AB∥CD,∠ABE=60°,∠D=50°,则∠E的度数为C
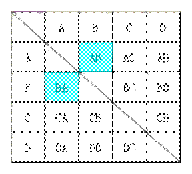
A.30° B.20° C.10° D.40°
答案:C
解析:两直线平行,同位角相等,所以,∠CFB=∠ABE=60°,
三角形的一个外角等于与它不相邻的两内角和,所以,∠CFB=∠D+∠E,
所以,∠E=10°,选C。
3.解分式方程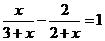 时,去分母后可得到C
时,去分母后可得到C
A.x(2+x)-2(3+x)=1 B. x(2+x)-2=2+x
C. x(2+x)-2(3+x)=(2+x)(3+x) D.x-2(3+x)=3+x
答案:C
解析:去分母后,注意等号的右边要乘以公分母(3+x)(2+x),所以,C正确。
4.计算 的结果是B
的结果是B
A.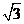 +
+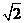 B.
B. 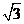 C.
C.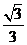 D.
D. 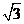 -
-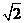
答案:B
解析:原式=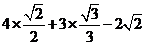 =
=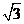
5.四川雅安发生地震灾害后,某中学九(1)班学生积极捐款献爱心,如图所示是该班50名学生的捐款情况统计,则他们捐款金额的众数和中位数分别是B
A.20,10 B.10,20 C.16,15 D.15,16

答案:B
解析:捐10元的学生最多,因此,众数为10元,捐5元、10元、15元的人数共有35人>25人,捐5元和10元的共有20人<25人,故中位数为20元。
6、如图,在△ABC中,BC>AC,点D在BC上,且DC=AC,角∠ACB的平分线CE交AD于E,点F是AB的中点,则S△AEF S四边形BDEF为D
S四边形BDEF为D
A.3:4 B.1:2 C.2:3 D.1:3
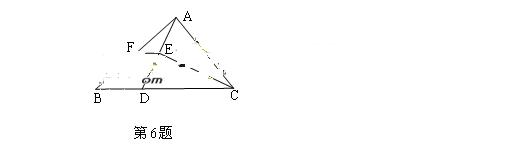
答案:D
解析:因为DC=AC,CE为角平分线,所以,E为AD中点,又F为AB中点,所以,EF为三角形ABD的中位线,△AEF∽△ADB,所以, ,S△AEF
,S△AEF S四边形BDEF=1:3,选D。
S四边形BDEF=1:3,选D。
7.体育课上,20人一组进行足球比赛,每人射点球5次,已知某一组的进球总数为49个,进球情况记录如下表,其中进2个球的有x人,进3个球的有y人,若(x,y)恰好是两条直线的交点坐标,则这两条直线的解析式是D
进球数 | 0 | 1 | 2 | 3 | 4 | 5 |
人数 | 1 | 5 | x | y | 3 | 2 |
A.y=x+9与y=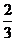 x+
x+ B. y=-x+9与y=
B. y=-x+9与y=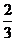 x+
x+
C. y=-x+9与y=-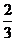 x+
x+ D. y=x+9与y=-
D. y=x+9与y=-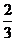 x+
x+
答案:C
解析:根据进球总数为49个得:2x+3y=49-5-3×4-2×5=22,整理得:y=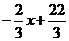
∵20人一组进行足球比赛,∴1+5+x+y+3+2=20,整理得:y=-x+9.故选C.
8.如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB'C',点B经过的路径为弧BB',若角∠BAC=60°,AC=1,则图中阴影部分的面积是A
A.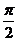 B.
B.  C.
C. 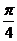 D.
D. 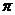

答案:A
解析:

9.将一边长为2的正方形纸片折成四部分,再沿折痕折起来,恰好能不重叠地搭建成一个三棱锥,则三棱锥四个面中最小的面积是C
A.1 B.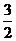 C.
C.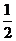 D.
D.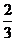
答案:C
解析:最小的一个面是等腰直角三角形,它的两条直角边都是2÷2=1,
1×1÷2=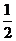 故三棱锥四个面中最小的面积是
故三棱锥四个面中最小的面积是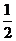 故选C.
故选C.
10.如图,在平面直角坐标系中,直线y=-3x+3与x轴、y轴分别交于A、B两点,以AB为边在第一象限作正方形ABCD沿x轴负方向平移a个单位长度后,点C恰好落在双曲线上则a的值是B
A.1 B.2 C.3 D.4
答案:B
解析:如图1,过点D作DE⊥x轴于点E.则∠DEA=∠AOB=90°,
∵四边形ABCD为正方形,∴∠BAD=90°,AB=DA,
∴∠2+∠3=90°,∵∠1+∠3=90°,∴∠1=∠2,∴△AOB≌△DEA,
∴ED=OA=1,EA=OB=3,∴OE=OA+EA=4 ∴点D的坐标为(4,1)
把D(4,1)代入y=  得: :k=4,∴所求的反比例函数关系式为y=
得: :k=4,∴所求的反比例函数关系式为y= 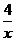
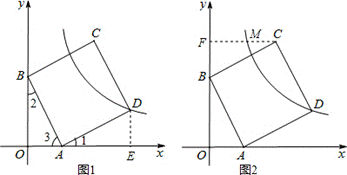
如图2,过点C作CF⊥y轴于点F,交双曲线于点M,
同(1)可得AOB≌△BFC,故CF=OB=3,BF=OA=1,∴C(3,4),
∵在反比例函数y=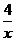 中,当y=4时,x=1,∴M(1,4),∵CM=CF-MF=3-1=2,
中,当y=4时,x=1,∴M(1,4),∵CM=CF-MF=3-1=2,
∴将正方形ABCD沿x轴向左平移2个单位长度时,点C恰好落在反比例函数的图象上.
二.填空题:
11.分解因式a3-ab2=
答案: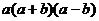
解析:原式=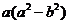 =
=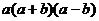
12.如图,在高度是21米的小山A处没得建筑物CD顶部C处的仰角为30°,底部D处的俯角为何45°,
则这个建筑物的高度CD= 米(结果可保留根号)
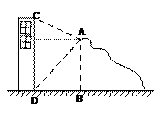
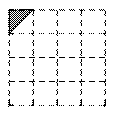

第12题图 第13题图 第14题图
答案: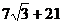
解析:过A作AE⊥CD于E,依题,得DE=AB=21,∠EAD=∠EDA=45°,所以,AE=DE=21,
∠CAE=30°,tan30°= ,解得:CE=
,解得:CE=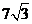 ,所以,CD=
,所以,CD=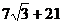
13.如图,是一个4×4的正方形网格,每个小正方形的边长为1.请你在网格中以左上角的三角形为基本图形,通过平移、对称或旋转变换,设计一个精美图案,使其满足:①既是轴对称图形,又是以点O为对称中心的中心对称图形;②所作图案用阴影标识,且阴影部分面积为4.
答案:

解析:本题答案不唯一,只要题目两个条件即可,上面五种图形中任选一个作答即可。
14如图,△ABC是斜边AB的长为3的等腰直角三角形,在△ABC内作第1个内接正方形A1B1D1E1(D1、E1在AB上,A1、B1分别在AC、BC上),再在△A1B1C内接同样的方法作第2个内接正方形A2B2D2E2,…如此下去,操作n次,则第n个小正方形AnBnDnEn 的边长是
答案:
解析:

15.若根式 有意义,则双曲线y=
有意义,则双曲线y= 与抛物线y=x2+2x+2-2k的交点在第 象限.
与抛物线y=x2+2x+2-2k的交点在第 象限.
答案:二
解析:由根式有意义,得: >0,即k<1,
>0,即k<1,

16.在实数范围内规定新运算“△”,其规则是:a△b=2a-b.已知不等式x△k≥1的解集在数轴上如图表示,则k的值是


第16题图 第17题图 第18题图
答案:k≤-3
解析:根据图示知,已知不等式的解集是x≤-1.
则2x-1≤-3 ∵x△k=2x-k≥1, ∴k≤2x-1≤-3,∴k≤-3.故答案是:k≤-3.
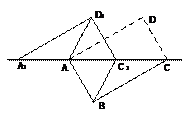
17.如图,△ACE是以□ABCD的对角线AC为边的等边三角形,点C与点E关于x轴对称.若E点的坐标是(7,-3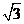 ),则D点的坐标是 .
),则D点的坐标是 .
答案:(5,0)
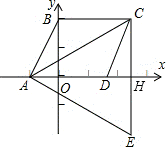
解析::∵点C与点E关于x轴对称,E点的坐标是(7,-3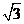 )
)
∴C的坐标为(7,3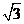 ) ∴CH=3
) ∴CH=3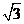 CE=6
CE=6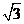
∵△ACE是以▱ABCD的对角线AC为边的等边三角形,
∴AC=6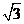 ,∴AH=9,∵OH=7,∴AO=DH=2,∴OD=5,∴D点的坐标是(5,0),故答案为(5,0).
,∴AH=9,∵OH=7,∴AO=DH=2,∴OD=5,∴D点的坐标是(5,0),故答案为(5,0).
18.如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1、BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B;②当x=1时,四边形ABC1D1是菱形;③当x=2时,△BDD1为等边三角形;④s=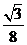 (x-2)2 (0<x<2);其中正确的是 (填序号).
(x-2)2 (0<x<2);其中正确的是 (填序号).
答案:①②③④
解析:①∵四边形ABCD为矩形,∴BC=AD,BC∥AD ∴∠DAC=∠ACB
∵把△ACD沿CA方向平移得到△A1C1D1,∴∠A1=∠DAC,A1D1=AD,AA1=CC1,
在△A1AD1与△CC1B中,
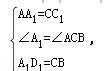 ∴△A1AD1≌△CC1B(SAS),故①正确;
∴△A1AD1≌△CC1B(SAS),故①正确;
②∵∠ACB=30°,∴∠CAB=60°,
∵AB=1,∴AC=2,∵x=1,∴AC1=1,∴△AC1B是等边三角形,∴AB=BC1,
又AB∥BC1,∴四边形ABC1D1是菱形,故②正确;
③如图所示:
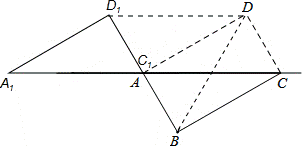
则可得BD=DD1=BD1=2,∴△BDD1为等边三角形,故③正确.
④易得△AC1F∽△ACD,

综上可得正确的是①②③④.故答案为:①②③④.
三.解答题:
19.用代入消元法解方程组
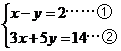
解析: 由①得: 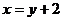 ……③
……③
代入②得: 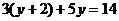
解之得: 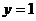
将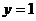 代入③得:
代入③得: 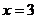
20.如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连结BE.请找出一对全等三角形,并说明理由.
解析: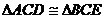 理由如下:
理由如下:
∵ 与
与 均为等腰直角三角形
均为等腰直角三角形
∴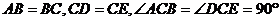
∴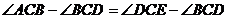
即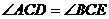
在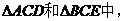

∴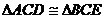 .
.
21.我市某中学为备战省运会,在校运动队的学生中进行了全能选手的选拔,并将参加选拔学生的综合成绩(得分为整数,满分为100分)分成四组,绘成了如下尚不完整的统计图表.
组别 | 成绩 | 组中值 |
|
第一组 | 90≤x<100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | m |
第三组 | 70≤x<80 | 75 | n |
第四组 | 60≤x<70 | 65 | 21 |
根据图表信息,回答下列问题:
(1)参加活动选拔的学生共有 人;表中m= ,n= ;
(2)若将各组的组中值视为该组的平均值,请你估算参加选拔学生的平均成绩;
(3)将第一组中的4名学生记为A、B、C、D,由于这4名学生的体育综合水平相差不大,现决定随机挑选其中两名学生代表学校参赛,试通过画树形图或列表的方法求恰好选中A和B 的概率.
解析:(1)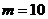
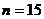
(2)
(3)由题意可列表如下:
由上表可知,挑选两名学生参赛共有12种方法,其可能性是均等的,因此恰好选中A和B的概率 =
=
22.已知:关于x的方程kx2-(3k-1)x+2(k-1)=0
(1)求证:无论k为何实数,方程总有实数根;
(2)若此方程有两个实数根x1,x2,且│x1-x2│=2,求k的值.
解析:(1)分两种情况讨论:
①当 =0 时,方程为x-2=0,∴x=2 方程有实数根
=0 时,方程为x-2=0,∴x=2 方程有实数根
②当 ≠0时,则一元二次方程的根的判别式
≠0时,则一元二次方程的根的判别式
△=[-(3 -1)]2-4
-1)]2-4 (2
(2 -2)=
-2)= 2+2
2+2 +1=(
+1=( +1)2≥0
+1)2≥0
∵不论 为何实数,△≥0成立,∴方程总有实数根。
为何实数,△≥0成立,∴方程总有实数根。
综合①②,可知 取任何实数,方程
取任何实数,方程 x2-(3
x2-(3 -1)x+2(
-1)x+2( -1)=0恒有实数根.
-1)=0恒有实数根.
(2)设x1、x2为抛物线y=  x2-(3
x2-(3 -1)x+2
-1)x+2 -2与x轴交点的横坐标.
-2与x轴交点的横坐标.
则有x1+x2=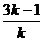 ,x1·x2=
,x1·x2=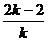
由| x1-x2|= =
=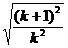 =
=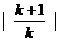 ,
,
由| x1-x2|=2得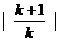 =2,∴
=2,∴ =1或
=1或 =
=
23.如图,AB为⊙O的直径,弦CD与AB相交于E,DE=EC,过点B的切线与AD的延长线交于F,过E作EG⊥BC于G,延长GE交AD于H.
(1)求证:AH=HD;(2)若cos∠C =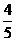 ,DF=9,求⊙O的半径.
,DF=9,求⊙O的半径.

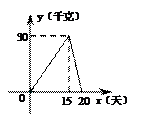

第23题图 图甲 图乙
第24题图
解析:(1)证明:∵AB为⊙O的直径,DE=EC,
∴ 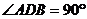 ,
,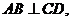
又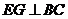
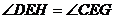
∴
∴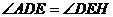 ∴
∴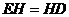
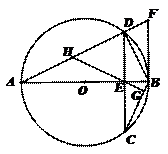
又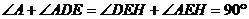
∴ ∴
∴
即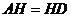
(2)解法一:
解:∵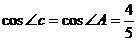 ,设
,设
∵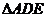 ∽
∽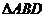 ∴
∴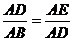 ∴
∴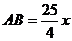
∵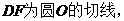 ∴AB⊥BF ∴ BF//CD
∴AB⊥BF ∴ BF//CD
∴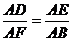 ∴
∴ 解之得
解之得
∴圆O的半径为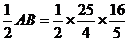 =10
=10
解法二:
解:∵AB为⊙O的直径, ∴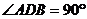
∵BF为⊙O的切线, ∴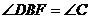
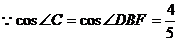 ,
, 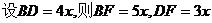
又 , ∵
, ∵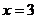 ∴
∴
∵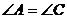 ∴
∴
设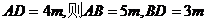 又
又
∴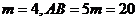
∴圆O的半径为10
24.某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记录,根据所记录的数据可绘制如图所示的函数图象,其中日销售量y(千克)与销售时间x(天)之间的函数关系如图甲所示,销售单价p(元/千克)与销售时间x(天)之间的函数关系如图乙所示.
(1)直接写出y与x之间的函数关系式;
(2)分别求出第10天和第15天的销售金额;
(3)若日销售量不低于24千克的时间段为“最佳销售期”,则此次销售过程中“最佳销售期”共有多少天?在此期间销售单价最高为多少元?
解析:
(1)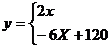
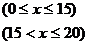
(2)当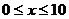 时, p与x之间的解析式为
时, p与x之间的解析式为
当 时,设其解析式为
时,设其解析式为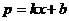
由图可知其图象过点(10,10),(20,8)
∴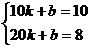 解之得
解之得 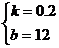

∴其函数解析式为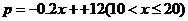
设销售金额为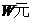
当
 (元)
(元)
当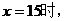
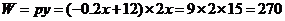 (元)
(元)
(3)当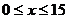 时, 由题意有
时, 由题意有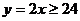 , 解之得
, 解之得
当 时, 由题意有
时, 由题意有 解之得
解之得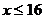
∴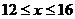
因此最佳销售期共有:16-12+1=5(天)
当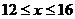
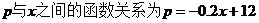
∵ ,∴
,∴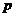 随
随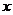 的增大而减小
的增大而减小
∴当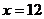 时,
时,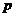 取最大值。此时
取最大值。此时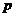 =
=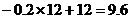 (元/千克)
(元/千克)
故最佳销售期共有5天,在此期间销售单价最高为9.6元。
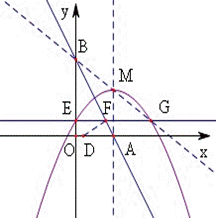
25. 已知:如图①,直线y=-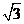 x+
x+ 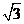 与x轴、y轴分别交于A、B两点,两动点D、E分别从A、B两点同时出发向O点运动(运动到O点停止);对称轴过点A且顶点为M的抛物线y=a(x-k)2+h (a<0) 始终经过点E,过E作EG∥OA交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分别是1个单位 长度/秒和
与x轴、y轴分别交于A、B两点,两动点D、E分别从A、B两点同时出发向O点运动(运动到O点停止);对称轴过点A且顶点为M的抛物线y=a(x-k)2+h (a<0) 始终经过点E,过E作EG∥OA交抛物线于点G,交AB于点F,连结DE、DF、AG、BG.设D、E的运动速度分别是1个单位 长度/秒和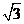 个单位长度/秒,运动时间为t秒.
个单位长度/秒,运动时间为t秒.
(1)用含t代数式分别表示BF、EF、AF的长;
(2)当t为何值时,四边形ADEF是菱形?判断此时△AFG与△AGB是否相似,并说明理由;
(3)当△ADF是直角三角形,且抛物线的顶点M恰好在BG上时,求抛物线的解析式.
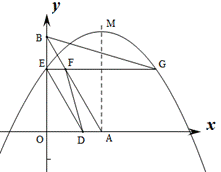
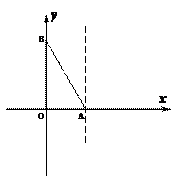
图① 图②
第25题图
解析:(1)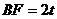 ,
, ,
,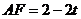 (
(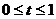 )
)
(2)①在
∴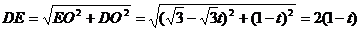
∵ ,
, ,
,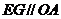 ∴四边形ADEF为平行四边形。
∴四边形ADEF为平行四边形。
若四边形ADEF为菱形,则有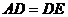
∴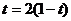 解之得
解之得
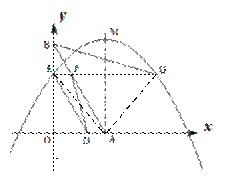
即当 时四边形ADEF为菱形。
时四边形ADEF为菱形。
②△AFG与△AGB相似,理由如下:
连接AE,在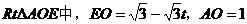
∴
由抛物线的对称称性可知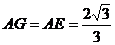
在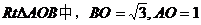 ∴
∴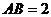
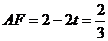
在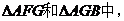 ∵
∵ ,
,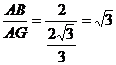
∴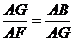 又
又
∴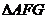 ∽
∽ 。
。
(3) ①当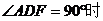 ,如图,则有DF//OB
,如图,则有DF//OB
∴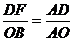 即
即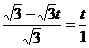 ∴
∴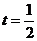 ,
,
(另:易证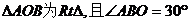
∴
∴ ,即F为AB的中点,
,即F为AB的中点,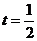 )
)
又由对称性可知EG=2AO=2
∴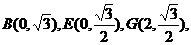
设直线BG的解析式为 ,把B、G两点的坐标代入有:
,把B、G两点的坐标代入有:
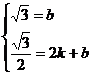 解之得
解之得 ∴
∴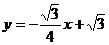
令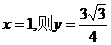 ,∴M(1,
,∴M(1,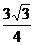 )
)
设所求抛物线的解析式为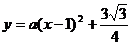 又
又
∴ 解之得
解之得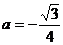
故所求解析式为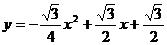
②当 ,如图,
,如图,
在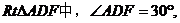
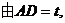 ∴
∴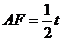 由(1)有
由(1)有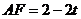
∴ 解之得:
解之得: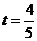
∴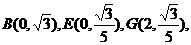
设直线BG的解析式为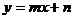 把B、G两点的坐标代入有:
把B、G两点的坐标代入有:
 解之得:
解之得: ∴
∴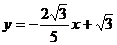
令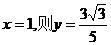 ,∴M(1,
,∴M(1,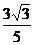 )
)
设所求抛物线的解析式为 又
又
∴ 解之得
解之得
故所求解析式为
综上所求函数的解析式为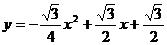 或
或

 频数
频数
