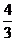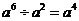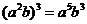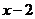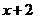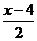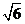(单词翻译:单击)
第一部分 选择题(共30分)
一、选择题(本大题共10小题,每小题3分,满分30分,在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 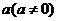 的相反数是
的相反数是 
A. | B. | C. | D. |
2.下列图形中,是中心对称图形的是 
A. | B. | C. | D. |
3.如图 ,在边长为
,在边长为 的小正方形组成的网格中,
的小正方形组成的网格中,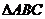 的三个顶点均在格点上,则
的三个顶点均在格点上,则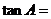

A. | B. | C. | D. |
4.下列运 算正确的是
算正确的是
A. | B. | C. | D. |
5.已知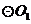 和
和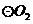 的半径分别为
的半径分别为 和
和 ,若
,若 ,则
,则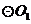 和
和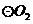 的位置关系是
的位置关系是
A. 外离 | B.外切 | C.内切 | D.相交 |
6.计算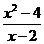 ,结果是
,结果是 
A. | B. | C. | D. |
7.在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是: ,
, ,
, ,
, ,
, ,
, ,
, ,
, .对这组数据,下列说法正确的是
.对这组数据,下列说法正确的是 
A. 中位数是 | B. 众数是 | C. 平均数是 | D. 极差是 |
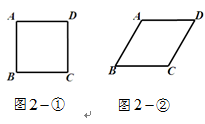
8.将四 根长度相等的细木条首尾相接,用钉
根长度相等的细木条首尾相接,用钉 子钉成四边形
子钉成四边形 ,转动这
,转动这 个四边形,使它形状改变.当
个四边形,使它形状改变.当 时,如图
时,如图 ①,测得
①,测得 .当
.当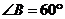 时,如图
时,如图 ②,
②,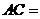
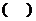
A. | B. | C. | D. |
9.已知正比例函数 的图象上两点
的图象上两点 、
、 ,且
,且 ,
, 则下列不等式中恒成立的是
则下列不等式中恒成立的是
A. | B. | C. | D. |
10.如图 ,四边形
,四边形 、
、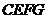 都是正方形,点
都是正方形,点 在线段
在线段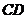 上,连接
上,连接 、
、 ,
, 和
和 相交于点
相交于点 .设
.设 ,
, .下列结论:①
.下列结论:① ;②
;②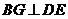 ;③
;③ ;④
;④ .其中结论正确的个数是
.其中结论正确的个数是 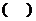
A. | B. | C. | D. |
第二部分 非选择题(共120分)
二、填空题(本大题共6小题,每小题3分,满分18分)
11. 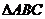 中,已知
中,已知 ,
,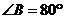 ,则
,则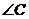 的外角的度数是
的外角的度数是
 .
.
12. 已知 是
是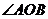 的平分线,点
的平分线,点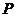 在
在 上,
上,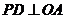 ,
, ,垂足分别为点
,垂足分别为点 、
、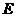 ,
, ,则
,则 的长
的长 度为
度为 .
.
13. 代数式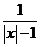 有意义时,
有意义时,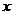 应满足的条件为
应满足的条件为 .
.
14. 一个几何体的三视图如图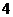 ,根据图示的数据计算该几何体的全面积为
,根据图示的数据计算该几何体的全面积为 .
.
(结果保留 )
)

15. 已知命题:“如果两个三角形全等,那么这两个三角形的面积相等.”写出它的逆命题: ,该逆命题是 命题(填“真”或“假”).
16. 若关于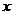 的方程
的方程 有两个实数
有两个实数 根
根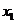 、
、 ,则
,则 的最小值为
的最小值为 .
.
三、解答题(本大题共9小题,满分102分,解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分9分)
解不等式: ,并在数轴上表示解集.
,并在数轴上表示解集.

18.(本小题满分9分)
如图 ,
, 的对角线
的对角线 、
、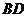 相交于点
相交于点 ,
,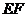 过点
过点 且与
且与 、
、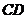 分别交于点
分别交于点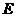 、
、 ,求证:
,求证: .
.

19.(本小题满分10分)
已知多项式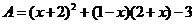
(1)化简多项式 ;
;
(2)若 ,求
,求 的值.
的值.
20.(本小题满分10分)
某校初三(1)班 名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:

(1)求 的值;
的值;
(2)若将各自选项目的 人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有 名男生,
名男生,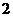 名女生.为了了解学生的训练效果,从这
名女生.为了了解学生的训练效果,从这 名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率.
名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率.
21.(本小题满分12分)
已知一次函数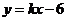 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于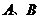 两点,点
两点,点 的横坐标为
的横坐标为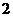 .
.
(1)求 的值和点
的值和点 的坐标;
的坐标;
(2)判断点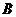 所在的象限,并说明理由.
所在的象限,并说明理由.
22.(本小题满分12分)
从广州到某市,可乘坐普通列车或高铁,已知高 铁的行驶路程是
铁的行驶路程是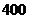 千米,普通列车的行驶路程是高铁的行驶路程的
千米,普通列车的行驶路程是高铁的行驶路程的 倍.
倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的 倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短
倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短 小时,求高铁的平均速度.
小时,求高铁的平均速度.
23.(本小题满分12分)
如图 ,
,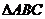 中,
中, ,
,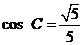 .
.
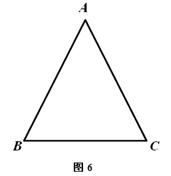
(1)动手操作:利用尺规作以 为直径的
为直径的 ,并标出
,并标出 与
与 的交点
的交点 ,与
,与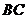 的交点
的交点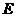 (保留作图痕迹,不写作法);
(保留作图痕迹,不写作法);
(2)综合应用:在你所作的图中,
①求证: ;
;
②求点 到
到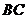 的距离。
的距离。
24.(本小题满分14分)
已知平面直角坐标系中两定点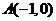 、
、 ,抛物线
,抛物线 过点
过点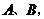 顶点为
顶点为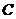 ,点
,点 为抛物线上一点.
为抛物线上一点.
(1)求抛物线的解析式和顶点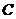 的坐标;
的坐标;
(2)当 为钝角时,求
为钝角时,求 的取值范围;
的取值范围;
(3)若 当
当 为直角时,将该抛物线向左或向右平移
为直角时,将该抛物线向左或向右平移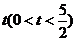 个单位,点
个单位,点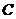 、
、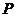 平移后对应的点分别记为
平移后对应的点分别记为 ,是否存在
,是否存在 ,使得首尾依次连接
,使得首尾依次连接 所构成的多边形的周长最短?若存在,求
所构成的多边形的周长最短?若存在,求 的值并说明抛物线平移的方向;若不存在,请说明理由.
的值并说明抛物线平移的方向;若不存在,请说明理由.
25.(本小题满分14分)

如图7,梯形 中,
中, ∥
∥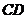 ,
, ,
, ,
, ,
,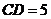 ,点
,点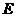 为线段
为线段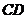 上一动点(不与点
上一动点(不与点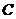 重合),
重合),
 关于
关于 的轴对称图形为
的轴对称图形为 ,连接
,连接 ,设
,设 ,
, 的面积为
的面积为 ,
, 的面积为
的面积为 .
.
(1)当点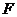 落在梯形
落在梯形 的中位线上时,求
的中位线上时,求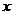 的值;
的值;
(2)试用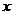 表示
表示 ,并写出
,并写出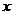 的取值范围;
的取值范围;
(3)当 的外接圆与
的外接圆与 相切时,求
相切时,求 的值.
的值.