(单词翻译:单击)
一、选择题(本大题共8个小题,每小题3分,满分24分)
1. -201 4的绝对值是()
4的绝对值是()
A.-2014 B .2014 C.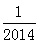 D. -
D. -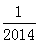
2.如图,已知a//b,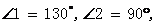 则
则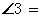 ()
()
A.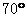 B.
B. 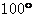 C.
C. 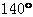 D.
D.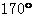
3.要反映我市某一周每天的最高气温的变化趋势,宜采用()
A.条形统计图 B.扇形统计图 C.折线统计图 D.频数分布直方图
4.若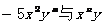 是同类项,则m+n的值为()
是同类项,则m+n的值为()
A.1  B.2 C.3 D.4
B.2 C.3 D.4
5.某几何体的主视图、左视图和俯视图分别如下图所示,则该几何体的体积为()
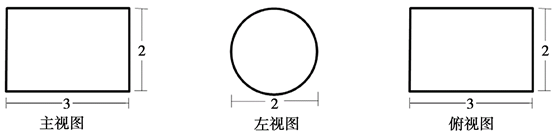
A.3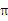 B.2
B.2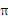 C.
C.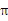 D.12
D.12
6.若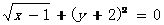 ,则
,则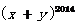 等于()
等于()
A.-1 B.1 C.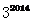
 D.-
D.-
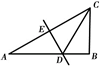
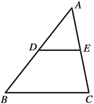
7.如图,在
 分别交AB、AC于D、E两点,若BD=2,则AC的长是()
分别交AB、AC于D、E两点,若BD=2,则AC的长是()
A.4 B.4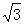 C .8 D.8
C .8 D.8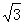
7、一个盒子里有完全相同的三个小球,球上分别标上数字-2、1、4.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是 ( )
A.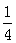 B.
B.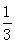 C.
C. D.
D.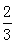
二、填空题(本大题共8个小题,每小题3分,满分24分)
9、我国第一艘航母“辽宁舰”的最大排水量为68050吨,用科学计数法表示这个数字是
10.如图,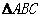 中,D、E分别为AB、AC的中点,则
中,D、E分别为AB、AC的中点,则 与
与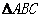 的面积比为.
的面积比为.
11、一组数据中4,13,24的权数分别是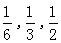 ,则这组数据的加权平均数是________.
,则这组数据的加权平均数是________.
12、已知一次函数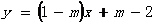 ,当m时,y随x的增大而增大。
,当m时,y随x的增大而增大。
1 3、已知☉
3、已知☉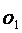 和☉
和☉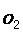 外切,圆心距为7cm, 若☉
外切,圆心距为7cm, 若☉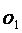 的半径为4cm,则☉
的半径为4cm,则☉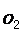 的半径是________cm
的半径是________cm
14、已知点A(m+2,3),B(-4,n+5)关于y轴对称,则m+n=__________.
15.已知关于x的方程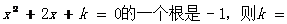 .
.
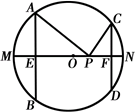
16、如图,AB、C D是半径为5的☉O的两条弦,AB=8,CD=6,MN是直径,AB
D是半径为5的☉O的两条弦,AB=8,CD=6,MN是直径,AB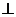 MN于点E,CD
MN于点E,CD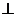 MN于点F,P为EF上的任意一点,则PA+PC的最小值为__________.
MN于点F,P为EF上的任意一点,则PA+PC的最小值为__________.
三、解答题(本大题共9个小题,共计72分)
17、(本小题6分)
计算: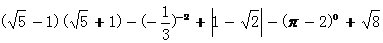
18.(本小题6分)先化简,再求值:
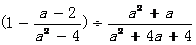 ,其中
,其中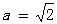
19.(本小题6分)利用对称变换可设计出美丽图案,在方格纸中有一个顶点都在格点上的四边形,且每个小正方形的边长都为1,完成下列问题:
(1)图案设计:先作出该四边形关于直线L成轴对称的图 形,再将你所作的图形和原四边形绕O点按顺时针旋转
形,再将你所作的图形和原四边形绕O点按顺时针旋转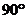 ;
;
(2)完成上述设计后,整个图案的面积等于.
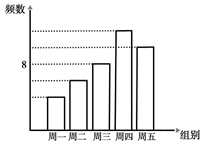
20,(本小题8分).某校八年级一班进行为期5天的图案设计比赛,作品上交时限为周一到周五,班委会将参赛作品逐天进行统计,并绘制成如图所示的频数直方图.已知从左到右各矩形的高度比为2:3:4:6:5,且已知周三组的频数是8.
(1)本次活动共收到件作品;
(2)若按各组所占百分比绘制成扇形统计图,那么周五组对应的扇形的圆心角是
度;
(3)本次活动共评出1个一等奖和2个二等奖,若将这三件作品进行编号并制作成背面完全相同的卡片,并随机抽出两张卡片,请你求出抽到的作品恰好一个一等奖、一个二等奖的概率.
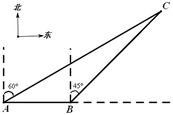
21.(本小题8分)如图:我国渔政船310船在南海海面上沿正东方向匀速航行,在A点观测到我渔船C在北偏东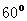 方向的我国某传统渔场捕鱼作业.若渔政310船航向不变,航行半小时后到达B点,观测我渔船C在东北方向上.问:渔政310船再按原航向航行多长时间,渔船C离渔政310船的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
方向的我国某传统渔场捕鱼作业.若渔政310船航向不变,航行半小时后到达B点,观测我渔船C在东北方向上.问:渔政310船再按原航向航行多长时间,渔船C离渔政310船的距离最近?(渔船C捕鱼时移动距离忽略不计,结果不取近似值.)
22.(本小题8分)国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,客户每购买一台可获得补贴500元,若同样用11万元购买此款空调,补贴后可购买的台数比补贴前多20%,则该款空调补贴前的售价为每台多少元?
23.(本小题8分)阅读材料:解分式不等式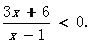
解:根据实数的除数法则:同号两数相除得正数,异号两数相除得负数,
因此,原不等式可转化为:(1)
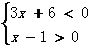 或
或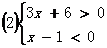
解(1)得:无解,解(2)得: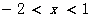
所以原不等式的解集是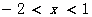
请仿照上述方法解下列分式不等式:
(1)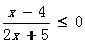 (2)
(2)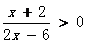
24. (本小题10分) 如图,在四边形ABCD中,AB=AD,CB=CD,AC与BD相交于O点,OC=OA,若E是CD上任意一点,连结BE交AC于点F,连结DF.
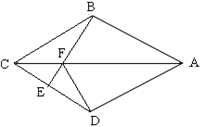
(1)证明:△CBF≌△CDF;
(2)若AC=2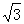 ,BD=2,求四边形ABCD的周长;
,BD=2,求四边形ABCD的周长;
(3)请你添加一个条件,使得∠EFD=∠BAD,并予以证明.
25.(本小题12分)如图,在平面直角坐标系中,O为坐标原点,抛物线过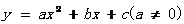 过O、B、C三点,B、C坐标分别为(10,0)和(
过O、B、C三点,B、C坐标分别为(10,0)和(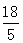 ,
, ),以OB为☉A经过C点,直线L垂直于X轴于点B.
),以OB为☉A经过C点,直线L垂直于X轴于点B.
(1)求直线BC的解析式;
(2)求抛物线解析式 及顶点坐标;
及顶点坐标;
(3)点M是☉A上一动点(不同于O,B),过点M作☉A的切线,交Y轴于点E,交直线L于点F,设线段ME长为m ,MF长为n,请猜想m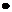 n的值,并证明你的结论.
n的值,并证明你的结论.
(4) 点P从O出发,以每秒1个单位速度向点B作直线运动,点Q同时从B出发,以相同速度向点C作直线运动,经过t(0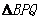 为等腰三角形,请求出满足条件的t值.
为等腰三角形,请求出满足条件的t值.
参考答案:
选择题 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | B | C | C | C | A | B | B | D |
二、填空题:
9、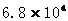 ; 10、1:4; 11、17; 12、〈1;
; 10、1:4; 11、17; 12、〈1;
13、3; 14、0; 15、1; 16、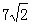
三、解答题:
17、解: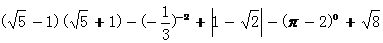
= …………5分(每算对一块给一分)
…………5分(每算对一块给一分)
=-7+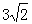 ………………………6分
………………………6分
18、解: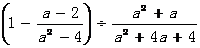
=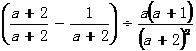 …
… ……………………2分
……………………2分
=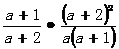 ………………………3分
………………………3分
= ………………………4分
………………………4分
 当a=
当a=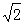 时,
时,
原式=
 =
=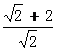 =
=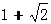 ………………………6分
………………………6分
19、(1)完成轴对称图形可得2分,完成旋转图形可得2分。
(2)20 ………………………2分
20、(1)40 ………………………2分
(2) ………………………4分
………………………4分
(3)设一等奖记为A,二等奖分别记为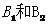 ,可用列表法表示如下(画树状图也行):
,可用列表法表示如下(画树状图也行):
A |
|
| |
A | (A, | (A, | |
| ( | ( | |
| ( | ( |
………………………6分
有6种情况,其中一个是一等奖,一个是二等奖的有4种,所以抽到的作品
恰好一个是一等奖,一个是二等奖的概率是p=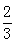 ………………………8分
………………………8分
21、解:设该款空调补贴前的售价为每台X元,根据题意,得:
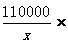 (1+20%)=
(1+20%)= ………………………2分
………………………2分
即 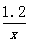 =
=
方程两边同乘以最简公分母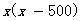 ,得
,得
1.2(x-500)=x ………………………4分
解得:x=3000 ………………………6分
检验:把x=3000代入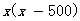 中,
中,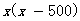 ≠0,
≠0,
因此x=3000是原方程的根.且符合题意.………………………7分
答:该款空调补贴前的售价为每台3000元. ………………………8分
22、解:作CD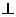 AB,交AB的延长线于D,则当渔政310船航行到D处时,
AB,交AB的延长线于D,则当渔政310船航行到D处时,
离C的距离最近.………………………1分
设CD长为x,
在Rt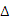 ACD中,
ACD中,
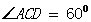 ,
,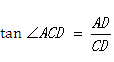
在Rt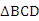 中,
中,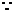
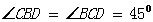 ,
,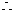 BD=CD=x
BD=CD=x
 ………………………3分
………………………3分
设渔政船从B航行到D需要t小时,则 ………………………4分
………………………4分
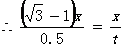
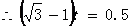 ………………………6分
………………………6分
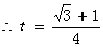 ………………………7分
………………………7分
答:渔政310船再航行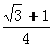 小时,渔政船C的距离最近. …………………8分
小时,渔政船C的距离最近. …………………8分
23、(1)解:根据实数的除数法则,异号两数相除,得负,
因此原不等式可转化为:(1)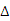

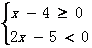 或(2)
或(2)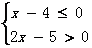 ……2分
……2分
解(1)得:无解; 解(2)得: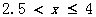 ………………………3分
………………………3分
所以原不等式的解集是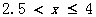 ………………………4分
………………………4分
(2)解:根据实数的除数法则,同号两数相除,得正,
因此原不等式可转化为:(1)
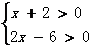 或(2)
或(2)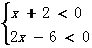 ………6分
………6分
解(1)得: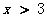 ; 解(2)得:
; 解(2)得: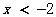 ………………………7分
………………………7分
所以原不等式的解集是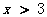 或
或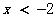 ………………………
………………………
24、(1)证明:在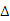 ABC和
ABC和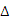 ACD中
ACD中
 CB=CD
CB=CD
AB=AD
CA=CA
 ABC
ABC ACD…………
ACD………… ……………1分
……………1分
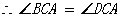 ………………………2分
………………………2分
在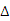 CBF和
CBF和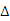 CDF中
CDF中
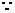 CB=CD
CB=CD
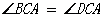
CF=CF
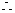
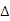 CBF
CBF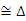 CDF………………………3分
CDF………………………3分
(2) CB=CD
CB=CD
又
 CO是等腰
CO是等腰
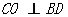 ,BO=DO
,BO=DO
又 CO=AO
CO=AO
 四边形ABCD是菱形 …………………………4分
四边形ABCD是菱形 …………………………4分
在Rt AOB中,
AOB中, AO=
AO=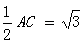 ,BO=
,BO=
 AB=
AB= ……………………………5分
……………………………5分
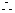 4AB=8
4AB=8
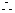 菱形ABCD的周长是8. …………………………6分
菱形ABCD的周长是8. …………………………6分
(3)第一种:添加BE 或
或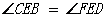 ……7分
……7分
证明: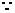
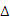 CBF
CBF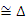 CDF
CDF
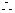
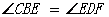
又 BE
BE
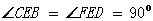
 CBE
CBE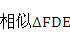 ………………………………9分
………………………………9分
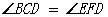
又 四边形ABCD是菱形
四边形ABCD是菱形
 ∠BCD=∠BAD
∠BCD=∠BAD
 ∠EFD=∠BAD……………………………………10分
∠EFD=∠BAD……………………………………10分
第二种: 添加 ……………………………………7分
……………………………………7分
证明:
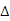 CBF
CBF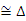 CDF
CDF
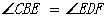
又

 CBE
CBE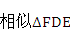
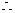
 ……………………………… 9分
……………………………… 9分
又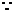 四边形ABCD是菱形
四边形ABCD是菱形
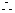 ∠BCD=∠BAD
∠BCD=∠BAD
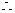 ∠EFD=∠BAD……………………………………10分
∠EFD=∠BAD……………………………………10分
25、(1)设直线BC解析式为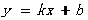 ………………1分
………………1分
把B(10,0)、C( )代入,
)代入,
得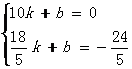 ……………………………………2分
……………………………………2分
分
解得: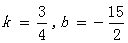
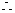 直线BC的解析式为
直线BC的解析式为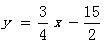 ………………………3分
………………………3分
(2)把O(0,0),B(10,0),C( )代入抛物线
)代入抛物线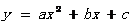 ,得
,得 ………………………………4分
………………………………4分
解得: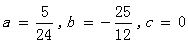
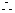 抛物线解析式为
抛物线解析式为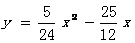 ………………………5分
………………………5分
顶点坐标为(5, )…………………………… 6分
)…………………………… 6分
(3)猜想: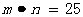 …………………………………7分
…………………………………7分
证明:连结AE、AM、AF.
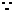 EF切 A于M,
EF切 A于M,
 AM
AM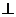 EF
EF
在Rt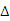 AOE和Rt
AOE和Rt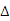 AME中,
AME中,
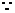
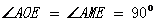
又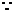 AM=AO,AE=AE
AM=AO,AE=AE
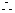 Rt
Rt  CBE
CBE
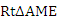
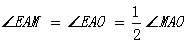
同理可证 Rt 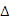 ABF
ABF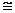
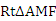
 …………………………… 8分
…………………………… 8分
易知: Rt  AME 相似
AME 相似
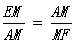
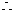
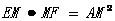 又AM=5
又AM=5
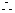
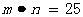 ……………………………………… 9分
……………………………………… 9分
(4)依题意有: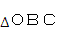 为Rt
为Rt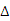 ,且
,且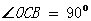
 BC=8,OB=10,OC=6
BC=8,OB=10,OC=6
 PB=10-t, BQ=t
PB=10-t, BQ=t
1. 当PB=QB时,10-t=t
解得 t=5 ……………………………………………… 10分
2. 当PQ=QB时,过Q作QD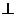 OB于D
OB于D
则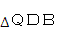
 相似
相似 OCB
OCB
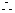

即 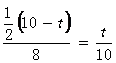
解得 t=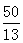 ………………………………………11分
………………………………………11分
3.当PB=PQ时,仿上法可求得t=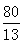 …………………12分
…………………12分

 )
)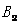 )
)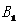
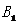 ,A)
,A)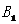 ,
, )
)
 ,A)
,A) ,
, )
)
