(单词翻译:单击)
一、精心选一选(本大题共8小题,每小题3分,满分24分.在每小题给出的四个选项中只有一项是符合题目要求的,请在答题卷上把正确答案的代号涂黑)
1.下列实数中,属于无理数的是( )
A.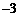 B.3.
B.3. 14 C.
14 C.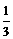 D.
D.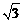
2.若代数式x+4的值是2,则x等于( )
A.2B.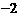 C.6D.
C.6D.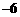
3.下列运算正确的是( ) 
 A.
A.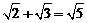 B.
B.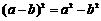
C.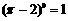 D.
D.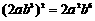
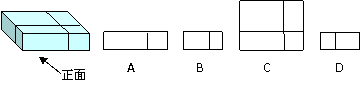
4.6月15日“父亲节”,小明送给父亲一个礼盒(如左图所示),该礼盒的主视图是( )
5.如图,l∥m,等边△ABC的顶点B在直线m上,∠1= 20°,则∠2的度数为(  )
)
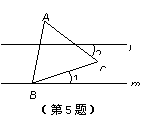
A.60° B.45° C.40° D.30°
B.45° C.40° D.30°
6.甲、乙、丙、丁四位同学五次数学测验成绩统计如右表所示.如果从这四位同学中,选出一位成绩较好且状态稳定的同学参加全国数学联赛,那么应选( )
甲 | 乙 | 丙 | 丁 | |
平均数 | 80 | 85 | 85 | 80 |
方 差 | 42 | 42 | 54 | 59 |
A.甲 B.乙 C.丙 D.丁
7.用一条长为40 cm的绳子围成一个面积为a cm2的长方形,a的值不可能为( )
A.20 B.40 C.100 D.120
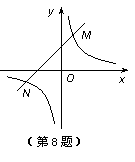
8.如图,双曲线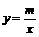 与直线
与直线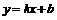 相交于点M,N,且点M的坐标为(1,3),点N的纵坐标为
相交于点M,N,且点M的坐标为(1,3),点N的纵坐标为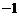 .根据图象
.根据图象
信息可得关于x的方程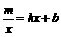 的解为( )
的解为( )
A.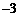 ,1 B.
,1 B.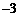 ,3 C.
,3 C.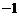 ,1 D.
,1 D.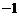 ,3
,3
二、细心填一填(本大题共8小题,每小题3分,满分24分.请把答案填在答题卷相应题号的横线上)
9.点P(1,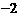 )关于 y轴对称的点的坐标为________.
)关于 y轴对称的点的坐标为________.
10.体育委员小金带了500元钱去买体育用品,已知一个足球x元,一个篮球y元.则代数式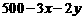 表示的实际意义是 __________.
表示的实际意义是 __________.
11.不等式组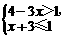 的解集是____________.
的解集是____________.
12.小亮与小明一起玩“石头、剪刀、布”的游戏,两同学同时出“剪刀”的概率是________.
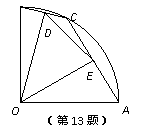
13.如图,在扇形OAB中,∠AOB=90°,点C是上的一个动点(不与A,B重合),OD⊥BC,OE⊥AC,垂足分别
为D,E.若DE=1,则扇形OAB的面积为________.
14.观察分析下列数据: 0,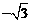 ,
,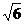 ,
,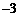 ,
, 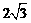 ,
,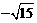 ,
, 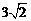 ,…,根据数据排列的规律得到第16个数据应是________(结果需化简) .
,…,根据数据排列的规律得到第16个数据应是________(结果需化简) .
15.科学家为了推测最适合某种珍奇植物生长的温度,将这种植物分别放在不同温度的环境中,经过一定时间后,测试出这种植物高度的增长情况,部分数据如下表:

温度t/℃ | -4 | -2 | 0 | 1 | 4 |
植物高度增长量l/mm | 41 | 49 | 49 | 46 | 25 |
科学家经过猜想、推测出l与t之间是二次函数关系.由此可以推测最适合这种植物生长的温度为________ ℃.
16.如图,在△ABC中,AB=AC =10,点D是边BC上一动点(不与B,C重合),∠ADE=∠B =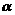 ,DE交AC于点E,
,DE交AC于点E,
且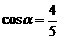 .下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,
.下列结论:①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,
BD为8或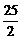 ;④
;④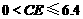 .其中正确的结论是______________.
.其中正确的结论是______________.

(把你认为正确结论的序号都填上)
三、专心解一解(本大题共8小题,满分72分.请认真读题,冷静思考.解答题应写出必要的文字说明、证明过程或演算步骤,请把解题过程写在答题卷相应题号的位置)
17.(本题满分8分,每小题4分)
(1)计算: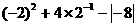 ; (2)化简:
; (2)化简: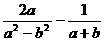 .
.
18.(本题满分7分)
随着市民环保意识的增强,烟花爆竹销售量逐年下降.咸宁市2011年销售烟花爆竹20万箱,到2013年烟花爆竹销售量为9.8万箱.求咸宁市2011年到2013年烟花爆竹年销售量的平均下降率.
19.(本题满分8分)
如图,在Rt△ABC中,∠ACB=90º,∠B=30º,将△ABC绕点C按顺时针方向旋转n度后,得到△DEC,点D刚好落在AB边上.
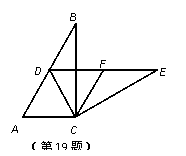
(1)求n的值;
(2)若F是DE的中点,判断四边形ACFD的形状,并说明理由.
20.(本题满分8分)
我市民营经济持续发展,2013年城镇民营企业就业人数突破20万.为了解城镇民营企业员工每月的收入状况,统计局对全市城镇民营企业员工2013年月平均收入随机抽样调查,将抽样的数据按 “2000元以内”、“2000元~4000元”、“4000元~6000元”和“6000元以上” 分为四组,进行整理,分别用A,B,C,D表示,得到下列两幅不完整的统计图.
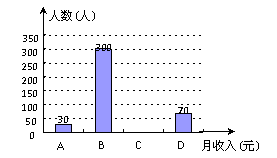
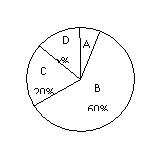
由图中所给出的信息解答下列问题:
(1)本次抽样调查的员工有_ __人,在扇形统计图中x的值为_ __,表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是_ __;
(2)将不完整的条形图补充完整,并估计我市2013年城镇民营企业20万员工中,每月的收入在“2000元~4000元”的约多少人?
(3)统计局根据抽样数据计算得到,2013年我市城镇民营企业员工月平均收入为4872元,请你结合上述统计的数据,谈一谈用平均数反映月收入情况是否合理?
21.(本题满分9分)
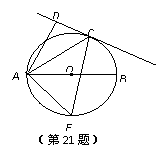
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AD⊥CD于点D.
(1) 求证: AC平分∠DAB;
(2) 若点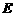 为的中点,
为的中点, 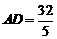 ,AC=8,求AB和CE的长.
,AC=8,求AB和CE的长.
22.(本题满分10分)
在“黄袍山国家油茶产业示范园”建设中,某农户计划购买甲、乙两种油茶树苗共1000株.已知乙种树苗比甲种树苗每株贵3元,且用100元钱购买甲种树苗的株数与用160元钱购买乙种树苗的株数刚好相同.
(1)求甲、乙两种油茶树苗每株的价格;
(2)如果购买两种树苗共用5600元,那么甲、乙两种树苗各买了多少株?
(3)调查统计得,甲、乙两种树苗的成活率分别为90%,95%.要使这批树苗的成活率不低于92%,且使购买树苗的费用最低,应如何选购树苗?最低费用是多少?
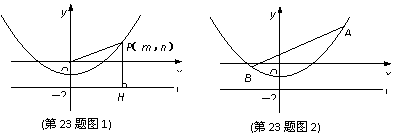
23.(本题满分10分)
如图1,P(m,n)是抛物线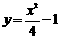 上任意一点, l是过点(0,
上任意一点, l是过点(0,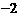 )且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
)且与x轴平行的直线,过点P作直线PH⊥l,垂足为H.
【探究】
(1)填空:当m=0时,OP=______,PH=______;当m=4时,OP=______,PH=______;
【证明】
(2)对任意m,n,猜想OP 与PH的大小关系,并证明你的猜想.
【应用】
(3)如图2,已知线段AB=6,端点A,B在抛物线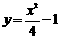 上滑动,求A,B两点到直线l的距离之和的最小值.
上滑动,求A,B两点到直线l的距离之和的最小值.
24.(本题满分12分)
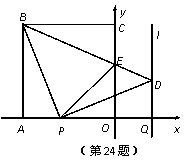
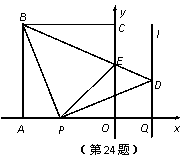
如图,正方形OABC的边OA,OC在坐标轴上,点B的坐标为(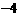 ,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与
,4).点P从点A出发,以每秒1个单位长度的速度沿x轴向点O运动;点Q从点O同时出发,以相同的速度沿x轴的正方向运动,规定点P到达点O时,点Q也停止运动.连接BP,过P点作BP的垂线,与过点Q平行于y轴的直线l相交于点D.BD与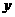 轴交于点E,连接PE.设点P运动的时间为t(s).
轴交于点E,连接PE.设点P运动的时间为t(s).
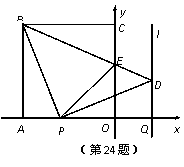
(1)∠PBD的度数为_________,点D的坐标为________(用t表示);
(2)当t为何值时,△PBE 为等腰三角形?
(3)探索△POE周长是否随时间t的变化而变化,若变化,说明理由;若不变,试求这个定值.
一.精心选一选(每小题3分,本大题满分24分)
题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
答案 | D | B | C | A | C | B | D | A |
二.细心填一填(每小题3分,本大题满分24分)
9.(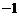 ,
,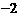 ) 10.体育委员买了3个足球,2个篮球后剩余的经费 11.
) 10.体育委员买了3个足球,2个篮球后剩余的经费 11.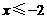
12.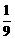 13.
13.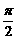 14.
14.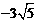 15.
15.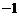 16.①②③④(少填不给分)
16.①②③④(少填不给分)
三.专心解一解(本大题满分72分)
17.(1)解:原式=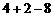 -----------------------------------------------------------------------3分
-----------------------------------------------------------------------3分
=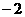 . -----------------------------------------------------------------4分
. -----------------------------------------------------------------4分
(2)解:原式=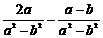 =
=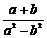 -------------------------------------------2分
-------------------------------------------2分
=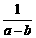 . ----------------------------------------------------------4分
. ----------------------------------------------------------4分
18.解:设年销售量的平均下降率为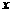 ,依题意得:
,依题意得:
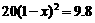 . ------------------------------------------------------------------3分
. ------------------------------------------------------------------3分
解这个方程,得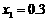 ,
,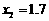 .-----------------------------------------------------5分
.-----------------------------------------------------5分
因为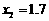 不符合题意,所以
不符合题意,所以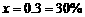 . -----------------------------------6分
. -----------------------------------6分
答:咸宁市2011年到2013年烟花爆竹年销售量的平均下降率为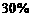 .---------------7分
.---------------7分
19.解:(1)由旋转可知,CA=CD.
∵∠ACB=90º,∠B=30º,∴∠A=60º.
∴△ACD为等边三角形.∴∠ACD=60º,即n=60. ----------------------------3分
(2)四边形ACFD是菱形. ---------------------------- ---------------------------------4分
---------------------------------4分
理由:∵F是DE的中点, ∴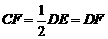 .
.
∵∠EDC=∠A=60º, ∴△FCD为等边三角形, ∴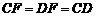 .
.
∵△ACD为等边三角形. ∴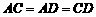 .
.
∴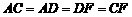 . ∴四边形ACFD是菱形. ------------------8分
. ∴四边形ACFD是菱形. ------------------8分
(说明:此题说理方法较多,如可以先说明是平行四边形再说明邻边,等)
20.(1)本次抽样调查的员工有 500 人, ------------------------------------------------1分
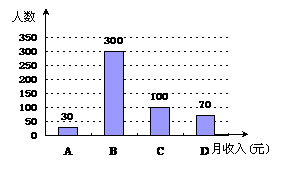
在扇形统计图中x的值 为 14 , ------------------------------2分
为 14 , ------------------------------2分
扇形圆心角的度数是 21.6 º ;
----------------------------------3分
(2)补充完整的条形图(如图)
-------------------------------------5分
20×60%=12(万人)
答:估计该市2013年城镇民营企业20万
员工每月的收入在“2000元~4000元”
的有12万人 ---------------------------6分
(3)用平均数反映月收入情况不合理.由数据可以看出500名被调查者中有330人的月收入不超过4000元,月收入的平均数受高收入者和低收入者收入变化的影响较大,月收入的中位数几乎不受高低两端收入变化的影响,因此,用月收入的中位数反映月收入水平更合理. -----------------------------------------------------------------8分
(本题答案不惟一,上述解法供参考.)
21.(1)证明:连结OC.
∵直线CD与⊙O相切于点C, ∴OC⊥CD.
∵AD⊥CD, ∴OC∥AD. ∴∠DAC=∠ACO.
∵OA =OC ∴∠OAC=∠ACO.
∴∠DAC=∠CAO.即AC平分∠DAB. ------------------------------------------------3分
(2)解:连接BC,
∵AB是⊙O的直径,∴∠ACB=90°=∠ADC.
∵∠D AC=∠CAO ,∴△ADC∽△ACB.
AC=∠CAO ,∴△ADC∽△ACB.
∴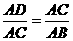 .
.
∵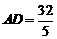 ,AC=8, ∴AB=10. -----------------------------------------------------------6分
,AC=8, ∴AB=10. -----------------------------------------------------------6分
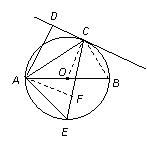 ∵点
∵点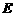 为的中点,∴∠ACE=45°.
为的中点,∴∠ACE=45°.
过点A作CE的垂线,垂足为F,
∴CF =AE=ACsin45°=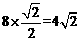 .
.
在Rt△ACB中,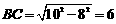 ,
,
∴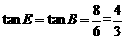 .
.
在Rt△AEF中,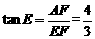 ,
,
∴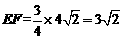 .
.
∴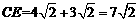 . ----------------------------------------------------9分
. ----------------------------------------------------9分
22.(1) 设甲种树苗每株x元,则乙种树苗每株(x+3)元.
根据题意得: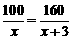 . -------------------------------------------------------1分
. -------------------------------------------------------1分
解得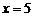 . ------------------------------------------------------------2分
. ------------------------------------------------------------2分
检验: 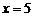 是原分式方程的解.
是原分式方程的解.
答:甲、乙两种油茶树苗每株的价格分别为5元和8元. --------------------------3分
(2)设购买甲种树苗x棵,购买乙种树苗为y棵,由题意得:
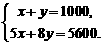
 ------------------------------------------------------4分
------------------------------------------------------4分
解得: 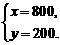 ------------------------------------------------------5分
------------------------------------------------------5分
答:购买甲种树苗800棵,乙种树苗200棵. ---------------------------------6分
(3)设购买甲种树苗x棵时,购买两种树苗的费用之和为w元.
则w与x的函数关系式为:
w=5x+8(1000-x)=8000-3x -----------------7分
由题意得:90%x+95%(1000-x)≥1000×92%,
解得x≤600. -------------------------------------8分
在w=8000-3x中,w随x的增大而减小,
所以当x=600时,w取得最小值,其最小值为8000-30×6 00=6200.-------9分
00=6200.-------9分
答:购买甲种树苗600棵,乙种树苗400棵费用最低,最低费用是6200元. -----10分
23.(1)填空:当m=0时,OP= 1 ,PH= 1 ;----------------------------------------1分
当m=4时,OP= 5 ,PH= 5 ;----------------------------------------3分
(2)OP= PH ------------------------------------------------------------------------------------4分
证明:∵P(m,n)是抛物线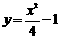 上任意一点,∴
上任意一点,∴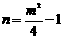 .
.
∵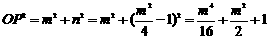 ,
,
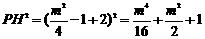 ,
,
∴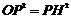 , ∴
, ∴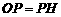 . ---------------------------------------------7分
. ---------------------------------------------7分
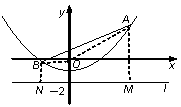 (3)分别A,B过点作直线l的垂线,垂足为M,N.
(3)分别A,B过点作直线l的垂线,垂足为M,N.
①当AB不过O点时,连接OA,OB,
在△OAB中OA+OB>AB=6,
由上述结论得:AM=OA,BN=OB.
∴AM+ BN>6.
②当AB过O点时,AM+ BN= OA+OB=AB=6.
所以AM+ BN的最小值为6.
即A,B两点到直线l的距离之和的最小值为6.-----------------------------10分
24.(1)∠PBD =45º ------------------------------------------------------------------------1分
点D的坐标为(t,t) --------------------------------------------------------------------3分
(2)解:由△PAB≌△DQP 得PB=PD,
显然PB≠PE.----------------------------------------------------------------------------4分
分两种情况:
(ⅰ)若EB=EP,则∠EPB=∠EBP=45 º,
此时点P与O点重合,t =4. -------------------------------------------------5分
(ⅱ)若BE=BP,则△PAB≌△ECB.
 ∴CE=PA= t.
∴CE=PA= t.
过D点作DF⊥OC于点F,
则DF=OF= t,
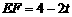 .
.
∵△BCE∽△DFE,
∴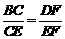 .
.
∴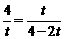 .
.
解得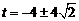 (负根舍去).
(负根舍去).
∴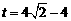 . ---------------------------------------------------------------7分
. ---------------------------------------------------------------7分
综上,当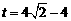 或4时,△PBE 为等腰三角形.--------------------------8分
或4时,△PBE 为等腰三角形.--------------------------8分
(3)△P OE周长不随时间
OE周长不随时间 t的变化而变化. ---------------------------------------------9分
t的变化而变化. ---------------------------------------------9分
将△BCE绕点B按顺时针方向旋转90 º,得到△BAH.
∴BE=BH, CE=AH,∠EBH =90º,
∴ ∠EBP=45º=∠PBH,
∠EBP=45º=∠PBH,
∵BP=BP,
∴△PBE≌△PBH .
∴EP= PH=AH+AP= CE+AP.
∴△POE周长=OP+OE+PE
=  OP+OE+ CE+AP
OP+OE+ CE+AP
=OA+OC
=4+4
=8. -----------------------------------------------------------------12分


