(单词翻译:单击)
第Ⅰ卷(选择题,共36分)
一、选择题(本大题共12小题,每小题3分,共36分)
1. 如果水位升高3m时水位变化记作+3m,那么水位下降3m时水位变化记作 ( )
如果水位升高3m时水位变化记作+3m,那么水位下降3m时水位变化记作 ( )
(A)-3m (B)3 m (C)6 m (D) -6 m
答案:A 由正数负数的概念可得。
考点:正数和负数(初一上学期-有理数)。
2. 下列图形中,是轴对称图形的是 ( )
下列图形中,是轴对称图形的是 ( )

(A) (B)  (C) (D)
(C) (D)
答案:D D有4条对称轴,也是中心对称图形。
考点:轴对称图形(初二上学期-轴对称图形)。
3. 南宁东高铁火车站位于南宁市青秀区凤岭北路,火车站总建筑面积约为267000平方米,其中数据267000用科学记数法表示为 ( )
(A)26.7×10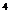 (B)2.67×10
(B)2.67×10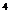 (C)2.67×10
(C)2.67×10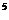 (D)0.267×10
(D)0.267×10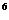
答案:C 由科学记数法的表示法可得。
考点:科学计数法(初一上学期-有理数)
4. 要使二次根式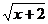 在实数范围内有意义,则实数
在实数范围内有意义,则实数 的取值范围是 ( )
的取值范围是 ( )
(A) >
>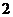 (B)
(B) ≥
≥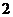 (C)
(C) >
>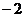 (D)
(D) ≥
≥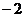
答案:D 由x+2≥0,可得。
考点:二次根式的双重非负性和不等式(初二上-二次根式,初一下-一元一次不等式)
5. 下列运算正确的是 ( )
(A)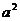 ·
·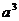 =
=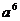 (B)
(B)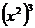 =
=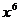 (C)
(C)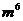 ÷
÷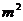 =
=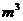 (D)6
(D)6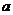 -4
-4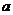 =2
=2
答案:B
考点:整式的加减乘除(初一上-整式的加减,初二上-整式的乘除和因式分解)
6. 在直径为200cm的圆柱形油槽内装入一些油以后,截面如图1所示,若油面的宽AB=160cm,则油的最大深度为 ( )
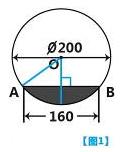
(A)40cm (B)60cm (C)80cm (D)100cm
答案:A
考点:垂径定理、勾股定理(初三上-圆,初二下-勾股定理)
【海壁分析】关键是过圆心O作半径垂直弦AB,并连结OA形成直角三角形
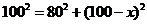 ,可得x=40
,可得x=40
7. 数据1,2,4,0,5,3,5的中位数和众数分别是 ( )
(A)3和2 (B)3和3 (C)0和5 (D)3和5
答案:D
考点:中位数和众数(初一上-统计)
8. 如图2所示把一张长方形纸片对折,折痕为AB,再以AB的中点O为顶点,把平角∠AOB三等分,沿平角的三等分线折叠,将折叠后的图形剪出一个以O为顶点的直角三角形,那么剪出的直角三角形全部展开铺平后得到的平面图形一定是 ( )

图2
(A)正三角形 (B)正方形 (C)正五边形 (D)正六边形
答案:A
考点:轴对称图形
【海壁分析】这道题非常新颖,让人眼前一亮。其实,在考场里面拿张草稿纸试一试,是最简单的方法。这个题目告诉我们,实践出真知。数学不仅仅需要动脑,也很需要动手。海壁教育向出题人致敬!
9. “黄金1号”玉米种子的价格为5元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子的价格打6折,设购买种子数量为 千克,付款金额
千克,付款金额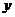 为元,则
为元,则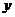 与
与 的函数关系的图像大致是 ( )
的函数关系的图像大致是 ( )

(A) (B) (C) (D)
答案:B
考点:一次函数:函数图像与分段函数(初二下-一次函数)
10. 如图3,已知二次函数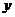 =
=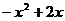 ,当
,当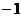 <
< <
<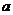 时,
时,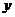 随
随 的增大而增大,则实数a的取值范围是 ( )
的增大而增大,则实数a的取值范围是 ( )
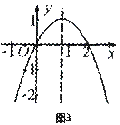
(A)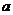 >
>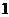 (B)
(B)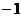 <
<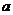 ≤
≤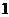
(C)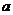 >0 (D)
>0 (D)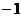 <
<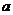 <
<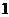
答案:B
考点:二次函数:对称轴和增减性(初三下-二次函数)
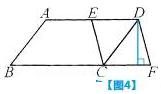
11. 如图4,在
 ABCD 中,点E是AD的中点,延长BC到点F,使CF : BC=1 : 2,连接DF,EC.若AB=5,AD=8,sinB=
ABCD 中,点E是AD的中点,延长BC到点F,使CF : BC=1 : 2,连接DF,EC.若AB=5,AD=8,sinB=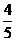 ,则DF的长等于 ( )
,则DF的长等于 ( )
(A)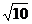 (B)
(B)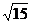 (C)
(C)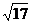 (D)
(D)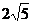
答案:C
考点:平行四边形的性质,勾股定理,三角函数(初二下-四边形,勾股定理,初三下-三角函数)
【海壁分析】关键是过点D 作△DCF的高,形成直角三角形。再通过平行四边形的性质、勾股定理和三角函数求解。这道题稍有综合性,但不算难。
作△DCF的高,形成直角三角形。再通过平行四边形的性质、勾股定理和三角函数求解。这道题稍有综合性,但不算难。
12. 已知点A在双曲线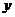
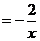 上,点B在直线
上,点B在直线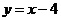 上,且A,B两点关于
上,且A,B两点关于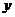 轴对称,设点A的坐标为(
轴对称,设点A的坐标为(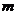 ,
,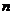 ),则
),则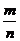 +
+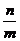 的值是 ( )
的值是 ( )
(A)-10 (B)-8 (C)6 (D)4
答案:A
考点:对称点,反比例函数和一次函数的性质,配方法(初二上-对称,初二下-一次函数和反比例函数,初二上-整式的乘除和因式分解)
【海壁分析】 此题相较以往的南宁中考压轴题,并不算难。解题的关键在于将A、B点的坐标通过m和n表示出来,代入各自的解析式中,再得到m和n的关系式,然后,对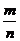 +
+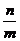 进行变形以配合刚才得到的关系式。变形的时候运用到了非常常用的配方的技巧。
进行变形以配合刚才得到的关系式。变形的时候运用到了非常常用的配方的技巧。
解答:∵A点的作标为(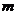 ,
,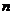 ),A,B两点关于y轴对称。∴点B 的坐标为(-
),A,B两点关于y轴对称。∴点B 的坐标为(-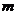 ,
,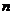 )
)
∵点A在双曲线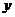
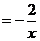 上 ∴
上 ∴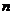 =
=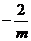 ∴
∴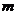
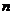 =
=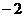
∵点B在直线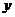
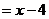 上 ∴
上 ∴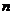 =-
=-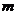 -4 ∴
-4 ∴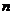 +
+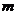 =-4
=-4
∴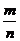 +
+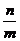 =
=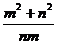 =
=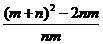 =-10
=-10
第Ⅱ卷(非选择题,共84分)
二、填空题(本大题共6小题,每小题3分,共18分)
13. 比较大小: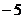
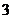 (填“>”“<”或“=”).<>
(填“>”“<”或“=”).<>
答案:<<>
考点:有理数大小的比较(初一上-有理数)
14. 如图5,已知直线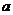 ∥
∥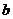 ,∠1=120°,则∠
,∠1=120°,则∠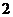 的度数是 °.
的度数是 °.
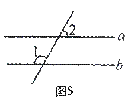
答案:60°
考点:平行线的性质;邻补角(初一下-平行于相交)
15. 因式分解: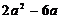 = .
= .
答案: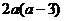
考点:因式分解(初二上-整式的乘除和因式分解)
16. 第45届世界体操锦标赛将于2014年10月3日至12日在南宁市隆重举行,届时某校将从小记者团内负责体育赛事报道的3名同学(2男1女)中任选2名前往采访,那么选出的2名同学恰好是一男一女的概率是 .
答案: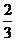
考点:概率(初三上-概率)
【海壁分析】男男,女男(一),女男(二),三选二,so easy!
17. 如图6,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于 海里.
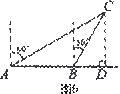
答案: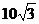
解答:BD设为 ,因为C位于北偏东30°,所以∠BCD=30°
,因为C位于北偏东30°,所以∠BCD=30°
在RT△BCD中,BD= ,CD=
,CD=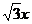 ,
,
又∵∠CAD=30°,在RT△ADC中,AB=20,AD=20+ ,
,
又∵△ADC≌△CDB,所以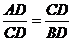 ,
,
即: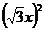 =
=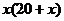 ,求出
,求出 =10,故CD=
=10,故CD=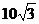 。
。
考点:三角函数和相似;
【海壁分析】这是一道典型的“解直角三角形”题,在2012年南宁中考出现在解答题中。关键是:作高,设x,利用特殊三角形三边关系用x表示出其它边,再根据三角函数、勾股定理或相似比等数量关系列出方程。这道题的方法非常多样。
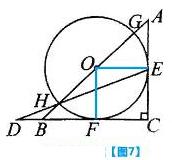
18. 如图7,△ ABC是等腰直角三角形,AC=BC=
ABC是等腰直角三角形,AC=BC=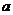 ,以斜边AB上的点O为圆心的圆分别与AC,BC相切与点E,F, 与AB 分别交于点G,H,且 EH 的延长线和 CB 的延长线交于点D,则 CD 的长为 .
,以斜边AB上的点O为圆心的圆分别与AC,BC相切与点E,F, 与AB 分别交于点G,H,且 EH 的延长线和 CB 的延长线交于点D,则 CD 的长为 .
答案: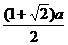
解答:连结OE,OF。∵AC、BC与圆O相切与点E,F,∴∠OEA=90°,∠OFC=90°
又∵△ABC是等腰直角三角形,∴∠ACB =90°,∠CBA=∠CAB=45°,AB=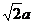
∵∠CBA=∠CAB=45°,且∠OEA=∠OFC=90°,OE=OF
∴△AOE和△BOF都是等腰直角三角形,且△AOE≌△BOF。∴AE=OE,AO=BO
∵OE=OF,∠OEC=∠OFC=∠ACB =90°∴四边形OEFC是正方形。∴OE=EC=AE=
=90°∴四边形OEFC是正方形。∴OE=EC=AE=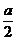
∵OE=OF,∴OA=OB=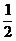 AB=
AB=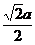 。OH=
。OH=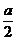 ,BH=
,BH=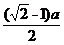
∵∠ACB=∠OEA =90°。∴OE∥DC,∴∠OED=∠EDC
∵OE=OH,∠OHE=∠OED=∠DHB=∠EDC,∴BD=BH=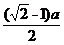
∴CD=BC+BH=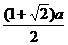
考点:等腰直角三角形,圆与直线相切,半径相等,三角形相似(初二上-对称,初三上-圆,初三下-相似)
【海壁分析】原题可转化为求DB的长度。DB所在的△BDH(BD=BH)(或证明△OEH∽△BDH亦可)是解题的突破口。所以,辅助线OE成为解题的入口。2013年,南宁中考的填空压轴题是等边三角形与内切圆,2014年,又出此题。是否意味着“圆与直角三角形”已经取代“找规律”,成为南宁中考填空压轴首选?
三、(本大题共2小题,每小题满分6分,共12分)
19. 计算: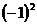
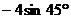
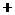
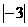
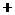
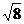
原式=1-4×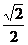 +3+
+3+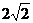 = 4
= 4
考点:负数的乘方;特殊角的三角函数值;绝对值;实数(初一上-有理数,初二上-二次根式,初三下-三角函数)
20. 解方程: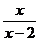
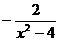
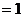
答案:去分母得: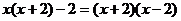
化简得:2 =-2,求得
=-2,求得 =-1
=-1
经检验: =-1是原方程的解
=-1是原方程的解
∴ 原方程的解是X=-1
考点:分式方程(初二下-分式)
【海壁分析】以前较常考的是分式的化简。
四、(本大题共2小题,每小题满分8分,共16分)
21. 如图8,△ABC三个顶点的坐标分别为A(1,1),
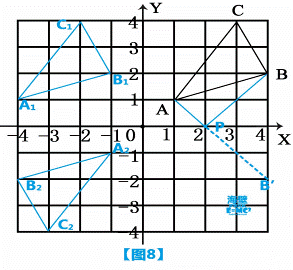
B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A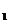 B
B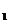 C
C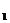 ;
;
(2) 请画出△ABC关于原点对称的△A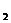 B
B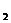 C
C ;
;
(3) 在 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
答案:(1)△A1B1C1如图所示;
(2)△A2B2C2如图所示;
(3)△PAB如图所示,点P的坐标为:(2,0)
考点:平面直角坐标系,图形的变化(平移、对称)(初一下-平面直角坐标系,初二上-对称)
【海壁分析】要使△PAB的周长最小,因为AB的长是固定的,一般转化为求“两条直线之和最小值”。这是海壁总结的三种最常见最值问题其中之一。主要方法是作线段某点关于该直线的对称点,然后连接对称点与线段另一点。
22. 考试前,同学们总会采用各种方式缓解考试压力,以最佳状态迎接考试. 某校对该校九年级的部分同学做了一次内容为“最适合自己的考前减压方式”的调查活动,学校将减压方式分为五类,同学们可根据自己的情况必选且只选其中一类,学校收集整理数据后,绘制了图 和图
和图 两幅不完整的统计图,请根据统计图中的信息解答下列问题:
两幅不完整的统计图,请根据统计图中的信息解答下列问题:
(1) 这次抽样调查中,一共抽查了多少名学生?
(2) 请补全条形统计图;
(3) 请计算扇形统计图中“享受美食”所对应扇形的圆心角的度数;
(4) 根据调查结果,估计该校九年级500名学生中采用“听音乐”的减压方式的人数.
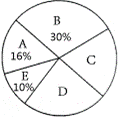

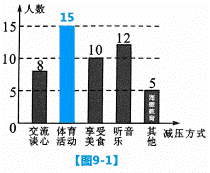
答案 (1)8÷16%= 50(名)
(2) 体育活动人数:50-8-10-12-5=15(名)(补全条形统计图如图所示)
(3) 360°×(10÷50)=72°
(4) 500×(12÷50)=120(名)
答:500名学生中估计采用“听音乐”的减压方式的学生人数为120名
考点:条形统计图,扇形统计图;抽样统计(初一下-统计)
【海壁分析】统计是南宁市中考数学的必考点。2012年统计里还包括概率的内容。
五、(本大题满分8分)
23. 如图10,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.
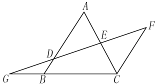
(1) 求证:△ADE≌△CFE;
(2) 若GB=2,BC=4,BD=1,求AB的长.
图10
答案:(1) ∵ AB∥FC,∴∠ADE=∠CFE
又∵∠AED=∠CEF,DE=FE
∴ △ADE≌△CFE(ASA)
(2) ∵ △ADE≌△CFE,∴ AD=CF
∵ AB∥FC,∴∠GBD=∠GCF,∠GDB=∠GFC
∴ △ GBD∽△GCF(AA)
∴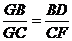
又因为GB=2,BC=4,BD=1,代入得:CF=3 = AD
∴ AB=AD+BD = 3+1 = 4
考点:平行线,三角形全等,相似(初一下-相交与平行,初二上-全等三角形,初三下-相似)
【海壁分析】简单的几何证明题每年都有,一般会以四边形为基础,利用三角形全等和相似的知识证明和计算。第一小题一般为证明题,第二小题一般为计算题。这类题相对简单,必须拿分。
六、(本大题满分10分)
24.“保护好环境,拒绝冒黑烟”.某市公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆. 若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1) 求购买A型和B型公交车每辆各需多少万元?
(2) 预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次. 若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客量总和不少于680万人次,则该公司有哪几种购车方案?哪种购车方案的总费用最少?最少总费用是多少?
答案:(1)设购买每辆A型公交车 万元,购买每辆B型公交车每辆
万元,购买每辆B型公交车每辆 万元,依题意列方程得,
万元,依题意列方程得,
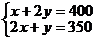 ,解得
,解得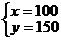
(2)设购买 辆A型公交车,则购买(10-
辆A型公交车,则购买(10- )辆B型公交车,依题意列不等式组得,
)辆B型公交车,依题意列不等式组得,
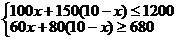
解得 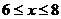
有三种方案
(一) 购买A型公交车6辆,B型公交车4辆
(二) 购买A型公交车7辆,B型公交车3辆
(三) 购买A型公交车8辆,B型公交车2辆
因A型公交车较便宜,故购买A型车数量最多时,总费用最少,即第三种购车方案最少 费用为:8
费用为:8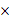 100+150
100+150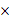 2=1100(万元)
2=1100(万元)
答:
(1)购买A型和B型公交车每辆各需100万元、150万元
(2)该公司有3种购车方案,第3种购车方案的总费用最少,最少总费用是 1
1 100万元。
100万元。
考点:二元一次方程组和一元一次不等式组。(初一下-二元一次方程组,初一下-一元一次不等式组)
【海壁分析】南宁中考数学每年都会有一道与实际结合的应用题,相较2010年(二元一次方程组和不等式),2011年(反比例函数和不等式),2012年(反比例函数和分式方程),2013年(含图像的一次函数及不等式)。今年的题目更加简单。海壁老师拿给备战期考的初一学生做,都能轻易做出来。
七、(本大题满分10分)
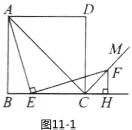
25. 如图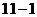 ,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
,四边形ABCD是正方形,点E是边BC上一点,点F在射线CM上,∠AEF=90°,AE=EF,过点F作射线BC的垂线,垂足为H,连接AC.
(1) 试判断BE与FH的数量关系,并说明理由;
 (2) 求证:∠ACF=90°;
(2) 求证:∠ACF=90°;
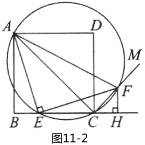
(3) 连接AF,过A,E,F三点作圆,如图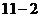 . 若EC=4,∠CEF=15°,求 AE 的长.
. 若EC=4,∠CEF=15°,求 AE 的长.
答案:
(1)BE=FH。理由如下:
∵四边形ABCD是正方形 ∴∠B=90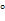 ,
,
∵FH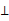 BC ∴∠FHE=90
BC ∴∠FHE=90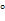
又∵∠AEF=90° ∴∠AEB+∠HEF=90° 且∠BAE+∠AEB=90°
 ∴∠HEF=∠BAE ∴ ∠AEB=∠E
∴∠HEF=∠BAE ∴ ∠AEB=∠E FH 又∵AE=EF
FH 又∵AE=EF
∴ △ABE≌△EHF(SAS)
∴BE=FH
(2)∵△ABE≌△EHF
∴BC=EH,BE=FH 又∵BE+EC=EC+CH ∴BE=CH
∴CH=FH
∴∠FCH=45°,∴∠FCM=45°
∵AC是正方形对角线,∴ ∠ACD=45°
∴∠ACF=∠FCM +∠ACD =90°
(3)∵AE=EF,∴△AEF是等腰直角三角形
△AEF外接圆的圆心在斜边AF的中点上。设该中点为O。连结EO,得∠AOE=90°
过E作EN⊥AC于点N
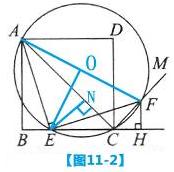
RT△ENC中,EC=4,∠ECA=45°,∴EN=NC=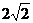
RT△ENA中,EN =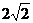
又∵∠EAF=45° ∠CAF=∠CEF=15°(等弧对等角)∴∠EAC=30°
∴AE=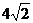
RT△AFE中,AE=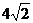 = EF,∴AF=8
= EF,∴AF=8
AE所在的圆O半径为4,其所对的圆心角为∠AOE=90°
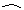 AE=2π·4·(90°÷360°)=2π
AE=2π·4·(90°÷360°)=2π
考点:正方形;等腰直角三角形;三角形全等;三角形的外接圆;等弧对等角,三角函数;弧长的计算。(初二上-全等三角形,轴对称,初二下-四边形,勾股定理;初三上-圆;初三下-三角函数)
【海壁分析】这道题前两小问考到了一个非常常见的几何模型“倒挂的直角”(在2012年压轴题中也出现过),在海壁的课堂中,给参加中考的学生讲过不下5次,这个模型经常用于全等和相 似的证明。在这里,用到了三角形全等中。
似的证明。在这里,用到了三角形全等中。
第三小问有一定的难度和综合性,关键是找出弧AE所对应的圆的半径和圆心角。结合第一、二小题的结论(在难题中,第一二小题的结论或次生结论往往是第三小题最重要的条件),所对应的圆是等腰直角△AEF的外接圆。圆心角不难找出,关键就是如何让EC=4与圆的半径结合起来,在这里,我们做了EN这条辅助线。(海壁教育认为,几何的难点无外乎两点:1、做辅助线,2、设x列方程)
八、(本大题满分10分)
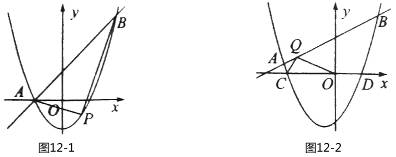
26. 在平面直角坐标系中, 抛物线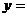
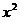 +
+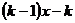 与直线
与直线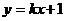 交于A, B两点,点A在点B的左侧.
交于A, B两点,点A在点B的左侧.
(1) 如图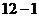 ,当
,当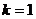 时,直接写出A,B两点的坐标;
时,直接写出A,B两点的坐标;
(2) 在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3) 如图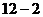 ,抛物线
,抛物线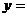
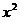 +
+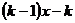
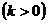 与
与 轴交于C,D两点(点C在点D的左侧).在直线
轴交于C,D两点(点C在点D的左侧).在直线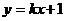 上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时
上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时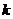 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
答案:(1)A(-1,0) ,B(2,3)
【解答,无需写】当k=1时,列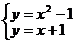 ,解可得
,解可得
(2)平移直线AB得到直线L,当L与抛物线只有一个交点时,△ABP面积最大【如图12-1(1)】
设直线L解析式为: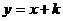 ,
,
根据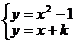 ,得
,得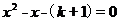
判别式△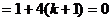 ,解得,
,解得,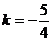
代入原方程中,得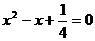 ;解得,
;解得,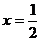 ,
,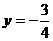
∴P(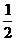 ,
,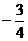 )
)
易求,AB交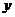 轴于M(0,1),直线L交轴
轴于M(0,1),直线L交轴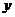 于G(0,
于G(0,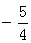 )
)
过M作MN⊥直线L于N,∵OM=1,OA=1,∴∠AMO=45°
∵∠AMN=90,∴∠NMO=45°
在RT△MNE中,∠NMO=45°,MG=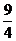 ,【如图12-1(2)】
,【如图12-1(2)】
∴ MN=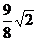 ,MN即为△ABP的高
,MN即为△ABP的高
由两点间距离公式,求得:AB=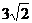
故△ABP最大面积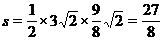
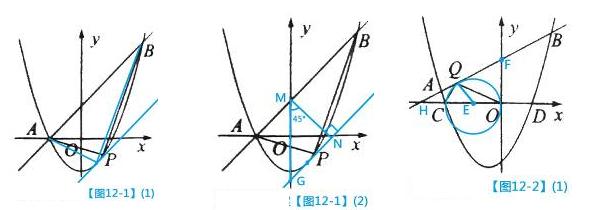
(3)设在直线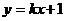 上存在唯一一点Q使得∠OQC=90°
上存在唯一一点Q使得∠OQC=90°
则点Q为以OC的中点E为圆心,OC为直径形成的圆E与直线
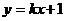 相切时的切点【如图12-2(1)】
相切时的切点【如图12-2(1)】
由解析式可知:C(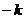 ,0),OC=
,0),OC=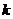 ,则圆E的半径:OE=CE=
,则圆E的半径:OE=CE=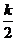 =QE
=QE
设直线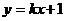 与
与 、
、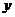 轴交于H点和F点,与,
轴交于H点和F点,与,
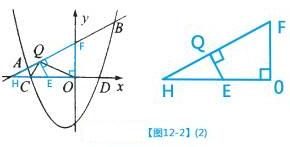 则F(0,1),∴OF=1 则H(
则F(0,1),∴OF=1 则H(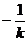 ,0), ∴OH =
,0), ∴OH =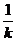
∴ EH=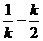
∵AB为切线 ∴EQ⊥AB,∠EQH=90°
在△FOH和△EQH中 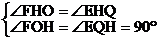
∴△FOH∽△EQH
∴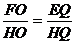 ∴ 1:
∴ 1: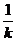 =
=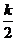 :QH,∴QH =
:QH,∴QH =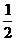
在RT△EQH中,EH=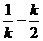 ,QH =
,QH =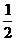 ,QE =
,QE =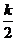 ,根据勾股定理得,
,根据勾股定理得,
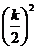 +
+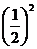 =
=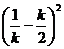
求得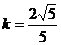
考点:一次函数、二次函数、简单的二元二次方程组、一元二次方程根的判别式、平面直角坐标系中的平行与垂直,直角三角形,圆(相切、圆心角)(初一下-平面直角坐标系,初二下-勾股定理,一次函数,初三上-一元二次方程,圆,初三下-二次函、相似三角形)
【海壁分析】延续了南宁市一贯的出题风格,本次考试的压轴题选择了二次函数综合题。
第一小题考查了二次函数与一次函数的交点(以前一般是求解析式),并不难,数学等级在B以上的都应该拿分,而且这个分比拿选择、填空最后一题的分要容易的多,看到很多同学不做,我们感到十分可惜。
第二小题也没有出乎我们的预料,命题者选择了三种最值问题中的第二种,重点考察是否了解通过平行线求最值的思路。在海壁的课堂上,这种题型我们做过专题的分析,我相信参加中考的海壁同学都能拿分。其实,求出P点以后,用点线距公式来解更加简单。
最后一小题,据我们了解,得分的不多,跪的多,第一难在理解,“是否存在唯一一点Q,使得∠OQC=90°”,这句话让很多人彻底凌乱,很少人能联想到圆的切点。第二,这个题和其他的“存在问题”又有不同,一般的存在问题是通过设点的坐标来表示线段的长度,而这道题却是用已经存在的参数k来表示线段的长度,这又是一点区别,第三,答案的得数是一个无理数,含有根号,这样就会让计算难度增大极多。综上,海壁教育认为,第三小问在南宁能答对的人不会超过千分之一。海壁预测,2015年,整套试卷的题目难度会降低,最后一题重点复习“动点问题”。


