一、选择题（每小题4分，共24分）

1．计算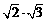的结果是（ ）．

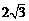(A) ； (B) ； (C) ； (D) ．

2．据统计，2013年上海市全社会用于环境保护的资金约为60 800 000 000元，这个数用科学记数法表示为（ ）．

(A)608×108； (B) 60.8×109； (C) 6.08×1010； (D) 6.08×1011．

3．如果将抛物线y＝x2向右平移1个单位，那么所得的抛物线的表达式是（ ）．

(A) y＝x2－1； (B) y＝x2＋1； (C) y＝(x－1)2； (D) y＝(x＋1)2．

4．如图，已知直线a、b被直线c所截，那么∠1的同位角是（ ）．

(A) ∠2； (B) ∠3； (C) ∠4； (D) ∠5．

5．某事测得一周PM2.5的日均值（单位：）如下：

50， 40， 75， 50， 37， 50， 40 ，这组数据的中位数和众数分别是（ ）．

(A)50和50； (B)50和40； (C)40和50； (D)40和40．

6．如图，已知AC、BD是菱形ABCD的对角线，那么下列结论一定正确的是（ ）．

(A)△ABD与△ABC的周长相等；

(B)△ABD与△ABC的周长相等；

(C)菱形的周长等于两条对角线之和的两倍；

(D)菱形的面积等于两条对角线之积的两倍．

二、填空题（每小题4分，共48分）

7．计算：a(a＋1)＝_________．

8．函数的定义域是_________．

9．不等式组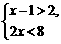的解集是_________．

10．某文具店二月份销售各种水笔320支，三月份销售各种水笔的支数比二月份增长了10%，那么该文具店三鱼粉销售各种水笔_________支．

11．如果关于x的方程x2－2x＋k＝0（k为常数）有两个不相等的实数根，那么k的取值范围是_________．

12．已知传送带与水平面所成斜坡的坡度i＝1∶2.4，如果它把物体送到离地面10米高的地方，那么物体所经过的路程为_________米．

13．如果从初三（1）、（2）、（3）班中随机抽取一个班与初三（4）班进行一场拔河比赛，那么恰好抽到初三（1）班的概率是_________．

14．已知反比例函数（k是常数，k≠0），在其图像所在的每一个象限内，y的值随着x的值的增大而增大，那么这个反比例函数的解析式是_________（只需写一个）．

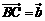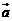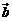15．如图，已知在平行四边形ABCD中，点E在边AB上，且AB＝3EB．设，，那么＝_________（结果用、表示）．

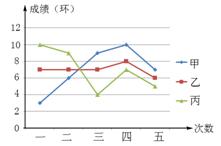
16．甲、乙、丙三人进行飞镖比赛，已知他们每人五次投得的成绩如图所示，那么三人中成绩最稳定的是_________．

17．一组数：2， 1， 3， x， 7， y， 23，…，满足“从第三个数起，前两个数依次为a、b，紧随其后的数就是2a－b”，例如这组数中的第三个数“3”是由“2×2－1”得到的，那么这组数中y表示的数为__________．

18．如图，已知在矩形ABCD中，点E在边BC上，BE＝2CE，将矩形沿着过点E的直线翻折后，点C、D分别落在边BC下方的点C′、D′处，且点C′、D′、B在同一条直线上，折痕与边AD交于点F，D′F与BE交于点G．设AB＝t，那么△EFG的周长为______________（用含t的代数式表示）．

三、解答题（本题共7题，满分78分）

19．（本题满分10分）

计算：．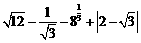

20．（本题满分10分）

解方程：．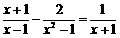

21．（本题满分10分，第（1）小题满分7分，第（2）小题满分3分）

已知水银体温计的读数y（℃）与水银柱的长度x（cm）之间是一次函数关系．现有一支水银体温计，其部分刻度线不清晰（如图），表中记录的是该体温计部分清晰刻度线及其对应水银柱的长度．

水银柱的长度x（cm）	4.2	…	8.2	9.8
体温计的读数y（℃）	35.0	…	40.0	42.0

（1）求y关于x的函数关系式（不需要写出函数的定义域）；

（2）用该体温计测体温时，水银柱的长度为6.2cm，求此时体温计的读数．

_ueditor_page_break_tag_22．（本题满分10分，每小题满分各5分）

如图，已知Rt△ABC中，∠ACB＝90°，CD是斜边AB上的中线，过点A作AE⊥CD，AE分别与CD、CB相交于点H、E，AH＝2CH．

（1）求sinB的值；

（2）如果CD＝，求BE的值．

23．（本题满分12分，每小题满分各6分）

已知：如图，梯形ABCD中，AD//BC，AB＝DC，对角线AC、BD相交于点F，点E是边BC延长线上一点，且∠CDE＝∠ABD．

（1）求证：四边形ACED是平行四边形；

（2）联结AE，交BD于点G，求证：．

24．（本题满分12分，每小题满分各4分）

在平面直角坐标系中（如图），已知抛物线与x轴交于点A(－1,0)和点B，与y轴交于点C(0,－2)．

（1）求该抛物线的表达式，并写出其对称轴；

（2）点E为该抛物线的对称轴与x轴的交点，点F在对称轴上，四边形ACEF为梯形，求点F的坐标；

（3）点D为该抛物线的顶点，设点P(t, 0)，且t＞3，如果△BDP和△CDP的面积相等，求t的值．

25．（本题满分14分，第（1）小题满分3分，第（1）小题满分5分，第（1）小题满分6分）

如图1，已知在平行四边形ABCD中，AB＝5，BC＝8，cosB＝，点P是边BC上的动点，以CP为半径的圆C与边AD交于点E、F（点F在点E的右侧），射线CE与射线BA交于点G．

（1）当圆C经过点A时，求CP的长；

（2）联结AP，当AP//CG时，求弦EF的长；

（3）当△AGE是等腰三角形时，求圆C的半径长．

图1 备用图

_ueditor_page_break_tag_

2014年上海市初中毕业统一学业考试数学试卷参考答案

选择题：

1.B

2.C

3.C

4.D

5.A

6.B

填空题：

7.a2+a

8.x≠1

9.3＜x＜4

10.352

11.k＜1

12.26

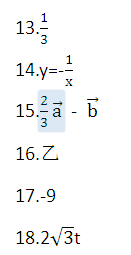
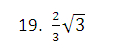
20.x=0
21. 37.5
22.BE=3

23题

24题

25题