(单词翻译:单击)
第Ⅰ卷(选择题,共36分)
一、选择题(本大题共12小题,每小题3分,共36分。)
1.(3分)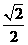 的相反数是( )
的相反数是( )
A. ﹣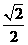 B.
B.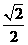 C. ﹣
C. ﹣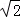 D.
D. 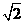

考点:实数的性质.
2.(3分) 一种微粒的半径是0.00004米,这个数据用科学记数法表示为( )
A. 4×106 B. 4×10﹣6 C. 4×10﹣5 D. 4×105

考点:科学记数法—表示较小的数.
3.(3分) 下列调查中,①调查本班同学的视力;②调查一批节能灯管的使用寿命;③为保证“神舟9号”的成功发射,对其零部件进行检查;④对乘坐某班次客车的乘客进行安检.其中适合采用抽样调查的是( )
A. ① B. ② C. ③ D. ④
【答案】B.
【解析】

考点:全面调查与抽样调查.
4.(3分) 如图,桌面上有一个一次性纸杯,它的正视图应是( )
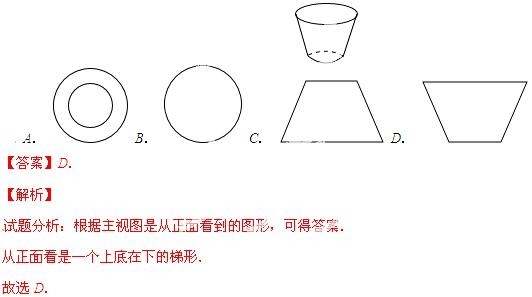
考点:简单几何体的三视图.
5.(3分) 在函数y=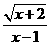 中,自变量x的取值范围是( )
中,自变量x的取值范围是( )
A. x≥﹣2且x≠1 B. x≤2且x≠1 C. x≠1 D. x≤﹣2

考点:函数自变量的取值范围.
6.(3分) 某班数学兴趣小组10名同学的年龄情况如下表:
年龄(岁) | 12 | 13 | 14 | 15 |
人数 | 1 | 4 | 4 | 1 |
则这10名同学年龄的平均数和中位数分别是( )
A. 13.5,13.5 B. 13.5,13 C. 13,13.5 D. 13,14

考点:1.中位数2.加权平均数.
7.(3分) 如图,⊙O是△ABC的外接圆,∠AOB=60°,AB=AC=2,则弦BC的长为( )
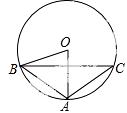
A. 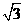 B. 3 C. 2
B. 3 C. 2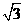 D. 4
D. 4

∴在直角△ABD中,BD=AB•sin60°=2×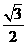 =
=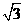 ,
,
∴BC=2 CD=2
CD=2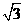 .
.
故选:C.
考点:1.垂径定理2.圆周角定理3.解直角三角形.
8.(3分) 按如图所示的程序计算,若开始输入的n值为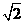 ,则最后输出的结果是( )
,则最后输出的结果是( )
A. 14 B. 16 C. 8+5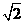 D. 14+
D. 14+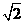
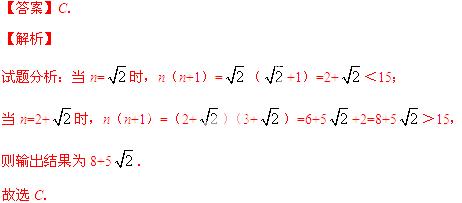
考点:实数的运算.
9.(3分) 若关于x的一元二次方程(k﹣1)x2+2x﹣2=0有不相等实数根,则k的取值范围是( )
A. k>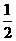 B. k≥
B. k≥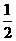 C. k>
C. k>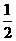
 且k≠1 D. k≥
且k≠1 D. k≥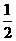 且k≠1
且k≠1

考点:1.根的判别式2.一元二次方程的定义.
10.(3分) 如图,Rt△ABC中,∠ACB=90°,AC=4,BC=6,以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E,则AD为( )
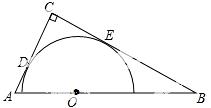
A. 2.5 B. 1.6 C. 1.5 D. 1
【答案】B.
【解析】

解得x=1.6,
故选B.
考点:1.切线的性质2.相似三角形的判定与性质.
11.(3分) 关于x的方程m(x+h)2+k=0(m,h,k均为常数,m≠0)的解是x1=﹣3,x2=2,则方程m(x+h﹣3)2+k=0的解是( )
A. x1=﹣6,x2=﹣1 B. x1=0,x2=5 C. x1=﹣3,x2=5 D. x1=﹣6,x2=2
【答案】 B.
B.
【解析】
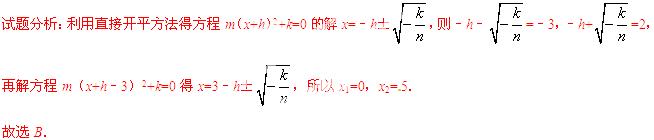
考点:解一元二次方程-直接开平方法.
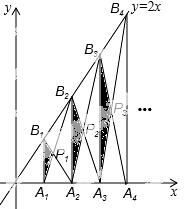
12.(3分) 如图,已知A1、A2、A3、…、An、An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1、 A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnA
A2、A3、…、An、An+1作x轴的垂线交直线y=2x于点B1、B2、B3、…、Bn、Bn+1,连接A1B2、B1A2、B2A3、…、AnBn+1、BnA n+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
n+1,依次相交于点P1、P2、P3、…、Pn.△A1B1P1、△A2B2P2、△AnBnPn的面积依次记为S1、S2、S3、…、Sn,则Sn为( )
A. 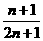 B.
B. 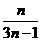 C.
C.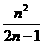 D.
D.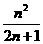

∴△A1B1P1∽△A2B2P1,
∴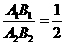 ,
,

考点:一次函数图象上 点的坐标特征.
点的坐标特征.
第Ⅱ卷(非选择题,共124分)
二、填空题(本大题共4小题,每小题5分,共20分)
13.(5分) a﹣4ab2分解因式结果是___________.

考点:提公因式法与公式法的综合运用.
1 4.(5分) 如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件:_________,使四边形ABCD为平行四边形(不添加任何辅助线).
4.(5分) 如图,在四边形ABCD中,对角线AC、BD交于点O,AD∥BC,请添加一个条件:_________,使四边形ABCD为平行四边形(不添加任何辅助线).
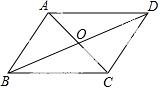
【答案】AD=BC.
【解析】
试题 分析:直接利用平行四边形的判定方法直接得出答案.
分析:直接利用平行四边形的判定方法直接得出答案.
当AD∥BC,AD=BC时,四边形ABCD为平行四边形.
故答案是AD=BC(答案不唯一).
考点:平行四边形的判定.
15.(5分) 有6张背面完全相同的卡片,每张正面分别有三角形、平行四边形、矩形、正方形、梯形和圆,现将其全部正面朝下搅匀,从中任取一张卡片,抽中正面画的图形是中心对称图形的概率为________.

考点:1.概率公式2.中心对称图形.
16.(5分) 如图,将若干个正三角形、正方形和圆按一定规律从左向右排列,那么第2014个图形是 .
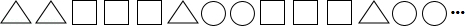

考点:图形的变化规律.
三、解答题(本大题共5小题,共44分,解答题应写出必要的文字说明或推演步骤。)
17.(8分) 计算:2tan60°﹣|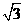 ﹣2|﹣
﹣2|﹣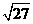 +(
+(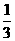 )﹣1.
)﹣1.

考点:1.实数的运算2.负整数指数幂3.特殊角的三角函数值.
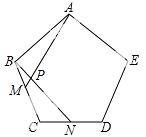
18.(9分) 如图,点M、N分别是正五边形ABCDE的边BC、CD上的点,且BM=CN,AM交BN于点P.
(1)求证:△ABM≌△BCN;
(2)求∠APN的度数.
【答案】(1)证明见解析;
(2)∠APN的度数为108°.
【解析】

∴∠CBN+∠ABP=∠APN=∠ABC=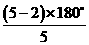 =108°.
=108°.
即∠APN的度数为108°.
考点:1.全等三角形的判定与性质2.多边形内角与外角.
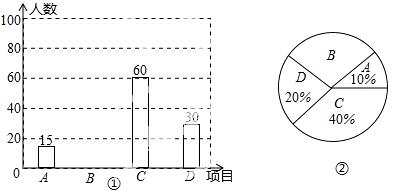
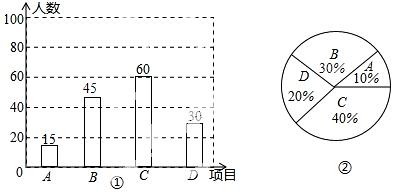
19.(9分) 为推广阳光体育“大课间”活动,我市某中学决定在学生中开设A:实心球.B:立定跳远,C:跳绳,D:跑步四种活动项目.为了了解学生对四种项目的喜欢情况,随机抽取了部分学生进行调查,并将调查结果绘制成如图①②的统计图.请结合图中的信息解答下列问题:
(1)在这项调查中,共调查了多少名学生?
(2)请计算本项调查中喜欢“立定跳远”的学生人数和所占百分比,并将两个统计图补充完整;
(3)若调查到喜欢“跳绳”的5名学生中有3名男生,2名女生.现从这5名学生中任意抽取2名学生.请用画树状图或列表的方法,求出
 刚好抽到同性别学生的概率.
刚好抽到同性别学生的概率.

画图如下:
(3)用A表示男生,B表示女生,画图如下:

共有20种情况,同性别学生的情况是8种,
则刚好抽到同性别学生的概率是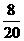 =
=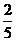 .
.
考点:1.条形统计图2.扇形统 计图3.列表法与树状图法.
计图3.列表法与树状图法.
20.(9分) “马航事件”的发生引起了我国政府的高度重视,迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机观测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为45°的方向上,请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值: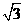 ≈1.7)
≈1.7)
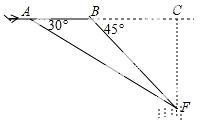
【答案】竖直高度CF约为1080米.
【解析】
试题分析:根据题意易得BC=CF,那么利用30°的正切值即可求得CF长.
试题解析:∵∠BDC=90°,∠DBC=45°,
∴BC=CF,
∵∠CAF=30°,
∴tan30°=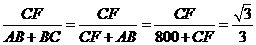 ,
,
解得:CF=400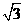 +400≈400(1.7+1)=1080(米).
+400≈400(1.7+1)=1080(米).
答:竖直高度CF约为1080米.
考点:解直角三角形的应用-仰角俯角问题.
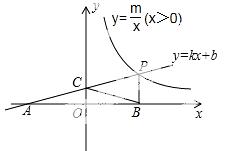
21.(9分) 如图,一次函数y=kx+b的图象与反比例函数y=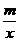 (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,且AC=BC.
(1)求一次函数、反比例函数的解析式;
(2)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,求出点D的坐标;如果不存在,说明理由.
【答案】(1)一次函数解析式为y=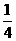 x+1,反比例解析式得:m=8,即反比例解析式为y=
x+1,反比例解析式得:m=8,即反比例解析式为y=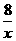 ;
;
(2)反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).
 【解析】
【解析】

将A(﹣4,0)与P(4,2)代入y=kx+b得: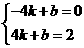 ,
,
解得:k=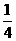 ,b=1,
,b=1,

对于一次函数y=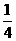 x+1,令x=0,得到y=1,即C(0,1),
x+1,令x=0,得到y=1,即C(0,1),
∴直线BC的斜率为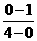 =﹣
=﹣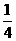 ,
,
设过点P,且与BC平行的直线解析式为y﹣2=﹣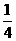 (x﹣4),即y=
(x﹣4),即y=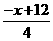 ,
,
与反比例解析式联立得: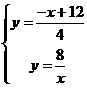 ,
,

则反比例函数图象上存在点D,使四边形BCPD为菱形,此时D坐标为(8,1).
考点:反比例函数综合题.
四、填空题(本大题共4小题,每小题6分,满分24分)
22.(6分) 已知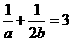 ,则代数式
,则代数式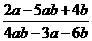 的值为____________.
的值为____________.

考点:分式的化简求值.
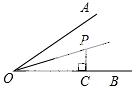
23.(6分) 如图,∠AOB=30°,OP平分∠AOB,PC⊥OB于点C.若OC=2,则PC的长是_________.
【答案】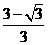 .
.
【解析】

∴QC=PQ+PC,即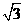 PC+PC=
PC+PC=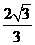 ,
,
解得:PC=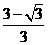 .
.
故答案是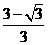 .
.
考点:1.含30度角的直角三角形2.勾股定理.
24.(6分) 已知实数x、y满足2x﹣3y=4,并且x≥﹣1,y<2,现有k=x﹣y,则k的取值范围是_______.

考点:1.解一元一次不等式2.一次函数的性质.
25.(6分) 通过对课本中《硬币滚动中的数学》的学习,我们知道滚动圆滚动的周数取决于滚动圆的圆心运动的路程(如图①).在图②中,有2014个半径为r的圆紧密排列成一条直线,半径为r的动圆C从图示位置绕这2014个圆排成的图形无滑动地滚动一圈回到原位,则动圆C自身转动的周数为__________.
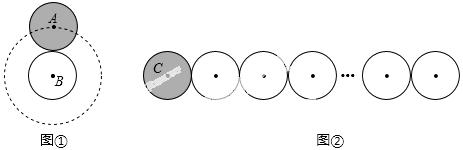

考点:1.弧长的计算2.相切两圆的性质.
五、解答题(本大题共3小题,每小题12分,共36分)
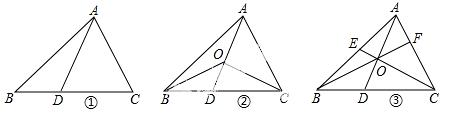
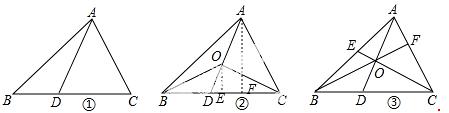
26.(12分) 如图,在△ABC中,D是BC边上的点(不与点B、C重合),连结AD.
问题引入:
(1)如图①,当点D是 BC边上的中点时,S△ABD:S△
BC边上的中点时,S△ABD:S△ ABC=_____;当点D是BC边上任意一点时,S△ABD:S△ABC=_____(用图中已有线段表示).
ABC=_____;当点D是BC边上任意一点时,S△ABD:S△ABC=_____(用图中已有线段表示).
探索研究:
 (2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
(2)如图②,在△ABC中,O点是线段AD上一点(不与点A、D重合),连结BO、CO,试猜想S△BOC与S△ABC之比应该等于图中哪两条线段之比,并说明理由.
拓展应用:
(3)如图③,O是线段AD上一点(不与点A、 D重合),连结BO并延长交AC于点F,连结C
D重合),连结BO并延长交AC于点F,连结C O并延长交AB于点E,试猜想
O并延长交AB于点E,试猜想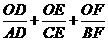 的值,并说明理由.
的值,并说明理由.
【答案】(1)1:2,BD:BC;
(2)S△BOC:S△ABC=OD:AD,理由见解析;
(3)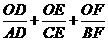 =1,理由见解析.
=1,理由见解析.
【解析】

∴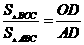 ;
;
(3)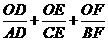 =1,理由如下:
=1,理由如下:
由(2)得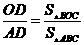 ,
,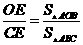 ,
,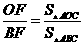 .
.
∴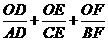 =
=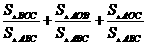 =
=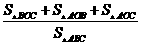 =1.
=1.
 .
.
考点:相似形综合题.
27.(12分) 某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定 再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?

99≤7.5x+6 (15﹣x)≤105.
(15﹣x)≤105.
解得: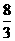 ≤x≤10.
≤x≤10.
因为x的正整数解为3,4,5,6,7,8,9,10,
所以共有8种进货方案;
(3)设总获利为W元.则:
W=(9﹣7.5)x+(8﹣6﹣a)(15﹣x)=(a﹣0.5)x+30﹣15a.
当a=0.5时,(2)中所有方案获利相同.
此时,购买A款汽车3辆,B款汽车12辆时对公司更有利.
考点:1.分式方程的应用2.一元一次不等式组的应用.
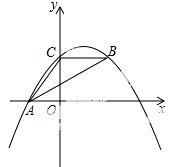
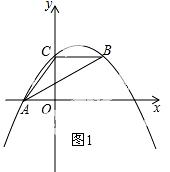
28.(12分) 如图,抛物线y=ax2+bx+c经过A(﹣3.0)、C(0,4),点B在抛物线上,CB∥x轴,且AB平分∠CAO.
(1)求抛物线的解析式;
(2)线段AB上有一动点P,过点P作y轴的平行线,交抛物线于点Q,求线段PQ的最大值;
(3)抛物线的对称轴上是否存在点M,使△ABM是以AB为直角边的直角三角形?如果存在,求 出点M的坐标;如果不存在,说明理由.
出点M的坐标;如果不存在,说明理由.

∵A(﹣3,0),C(0 ,4),
,4),
∴OA=3,OC=4.
∵∠AOC=90°,
∴AC=5.
∵BC∥AO,AB平分∠CAO,

∴抛物线的解析式为y=﹣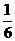 x2+
x2+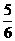 x
x +4;
+4;
(2)如图2,
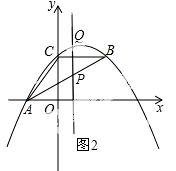
设直线AB的解析式为y=mx+n,
∵A(﹣3.0)、B(5,4)在直线AB上,
∴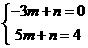

∴当t=1时,PQ取到最大值,最大值为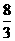 .
.
∴线段PQ的最大值为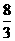 ;
;
(3) ①当∠BAM=90°时,如图3所示.
①当∠BAM=90°时,如图3所示.
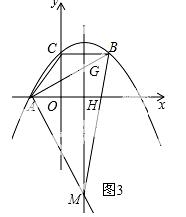
抛物线的对称轴为x=﹣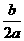 =﹣
=﹣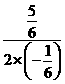 =
=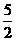 .
.

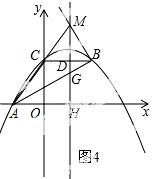
∵∠BDG=90°,BD=5﹣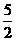 =
=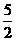 ,DG=4﹣
,DG=4﹣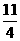 =
=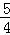 ,
,
∴BG=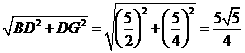 .
.



