(单词翻译:单击)
第Ⅰ卷(选择题,共36分)
一、选择题(本大题共12小题,每小题3分,共36分。)每小题都给出代号为 A、B、C、D的四个结论,其中只有一个是正确的,请用2B铅笔在答题卷上将选定的答案代号涂黑。
A、B、C、D的四个结论,其中只有一个是正确的,请用2B铅笔在答题卷上将选定的答案代号涂黑。
1.(2013年广西百色3分)-2013的相反数是【 】
A.-2013 B.2013 C. 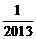 D.
D.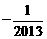
【答案】B。
2.(2013年广西百色3分)已知∠A=65°,则∠A的补角的度数是【 】
A.15° B.35° C.115° D.135°
【答案】C。
3.(2013年广西百色3分)百色市人民政府在2013年工作报告中提出,今年将继续实施十项为民办实事工程。其中教育惠民工程将投资2.82亿元,用于职业培训、扩大农村学前教育资源、农村义务教育学生营养改善计划、学生资助等项目。那么数据282 000 000用科学记数法(保留两个有效数字)表示为【 】
A.2.82×108 B.2.8×108 C.2.82×109 D.2.8×109
【答案】B。
4.(2013年广西百色3分)下列运算正确的是【 】
A.2a+3b=5ab B.3x2y-2x2y=1 C.(2 a2)3=6a6 D.5x3÷x2=5x
【答案】D。
5.(2013年广西百色3分)一个几何体的三视图如图所示,则该几何体的侧面展开图的面积为【 】
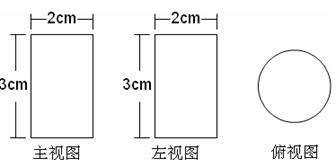
A.6cm2 B.4πcm2 C.6πcm2  D.9πcm2
D.9πcm2
【答案】B。
6.(2013年广西百色3分)在反比例函数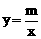 中,当x>0时,y随x的增大而增大,则二次函数y=m x2+m x的图象大致是下图中的【 】
中,当x>0时,y随x的增大而增大,则二次函数y=m x2+m x的图象大致是下图中的【 】
A.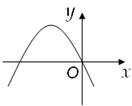 B.
B.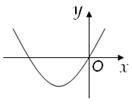 C.
C. 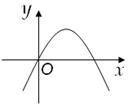 D.
D.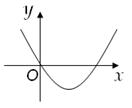
【答案】A。
7.(2013年广西百色3分)今年我市某县6月1日到10日的每一天最高气温变化如折线图所示,则这10个最高气温的中位数和众数分别是【 】
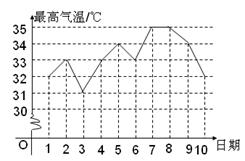
A.33℃ 33℃ B.33℃ 32℃ C.34℃ 33℃  D.35℃ 33℃
D.35℃ 33℃
【答案】A。
8.(2013年广西百色3分)如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是【 】
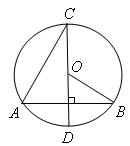
A.25° B.30° C.40° D.50°
【答案】C。
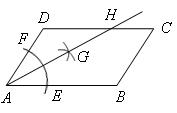
9.(2013年广西百色3分)如图,在平行四边形ABCD中,AB>CD,按以下步骤作图:以A为圆心,小于AD的长为半径画弧,分别交AB、CD于E、F;再分别以E、F为圆心,大于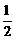 EF的长半径画弧,两弧交于点G;作射线AG交CD于点H。则下列结论:
EF的长半径画弧,两弧交于点G;作射线AG交CD于点H。则下列结论:
①AG平分∠DAB,②CH=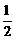 DH,③△ADH是等腰三角形,④S△ADH=
DH,③△ADH是等腰三角形,④S△ADH=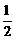 S四边形ABCH。
S四边形ABCH。
其中正确的有【 】
A.①②③ B.①③④ C.②④ D.①③
【答案】D。
10.(2013年广西百色3分)不等式组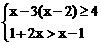 的解集在数轴上表示正确的是【 】
的解集在数轴上表示正确的是【 】
A.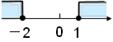 B.
B.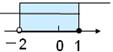 C.
C.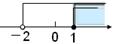 D.
D.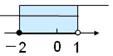
【答案】B。
11.(2013年广西百色3分)如图 ,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是【 】
,在矩形纸片ABCD中,AB=4,AD=3,折叠纸片使DA与对角线DB重合,点A落在点A′处,折痕为DE,则A′E的长是【 】
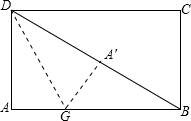
A.1 B.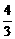 C.
C.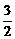 D.2
D.2
【答案】C。
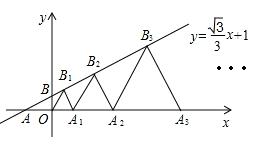
12.(2013年广西百色3分)如图,在平面直角坐标系中,直线l:y=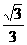 x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上。若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是【 】
x+1交x轴于点A,交y轴于点B,点A1、A2、A3,…在x轴上,点B1、B2、B3,…在直线l上。若△OB1A1,△A1B2A2,△A2B3A3,…均为等边三角形,则△A5B6A6的周长是【 】
A.24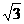 B.48
B.48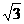 C.96
C.96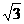 D.192
D.192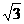
【答案】C。
第Ⅱ卷(非选择题,共84分)
二、填空题(本大题共6小题,每小题3分,共18分。)请把答案填在答题卷指定的位置上。
13.(2013年广西百色3分)4的算术平方根是___________ 。
【答案】2。
14.(2013年广西百色3分)若函数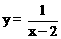 有意义,则自变量x的取值范围是_________。
有意义,则自变量x的取值范围是_________。
【答案】 。
。
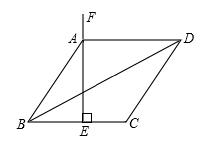
15.(2013年广西百色3分)如图,菱形ABCD的周长为12cm,BC的垂直平分线EF经过点A,则对角线BD的长是_________。
【答案】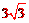 cm。
cm。
16.(2013年广西百色3分)某校对去年毕业的350名学生的毕业去向进行跟踪调查,并绘制出扇形统计图(如图所示),则该校去年毕业生在家 待业人数有_________人。
待业人数有_________人。
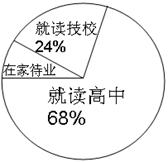
【答案】35。
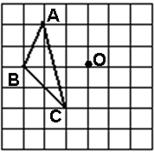
17.(2013年广西百色3分)如图,在方格纸中,每个小方格都是边长为1cm的正方形,△ABC的三个顶点都在格点上,将△ABC绕点O逆时针旋转90°后得到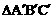 (其中A、B、C的对应点分别为
(其中A、B、C的对应点分别为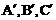 ),则点B在旋转过程中所经过的路线的长是 _________cm。(结果保留π)
),则点B在旋转过程中所经过的路线的长是 _________cm。(结果保留π)
【答案】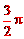 。
。
18.(2013年广西百色3分)如图,在边长10cm为的正方形ABCD中,P为AB边上任意一点(P不与A、B两点重合),连结DP,过点P作PE⊥DP,垂足为P,交BC于点E,则BE的最大长度为 _________ cm。
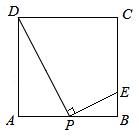
【答案】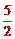 。
。
三、解答题(本大题共8小题,共66分)请在答题卷指定的位置上写出解答过程。
19.(2013年广西百色6分)计算: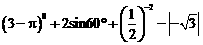
【答案】解:原式=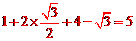 。
。
20.(2013年广西百色6分)先化简,再 求值:
求值: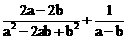 ,其中a=
,其中a=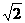 -1,b=
-1,b=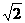 .
.
【答案】解:原式=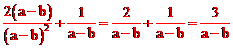 。
。
当a=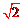 -1,b=
-1,b=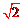 时,原式=
时,原式=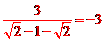 。
。
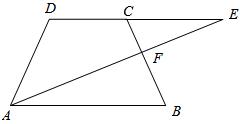
21.(2013年广西百色6分)如图,在等腰梯形ABCD中,DC∥AB,E是DC延长线上的点,连接AE,交BC于点F。
(1)求证:△ABF∽△ECF
(2)如果AD=5cm,AB=8cm,CF=2cm,求CE的长。
【答案】解:
(1)证明:∵DC∥AB,∴∠B=∠ECF,∠BAF=∠E,∴△ABF∽△ECF。
(2)∵在等腰梯形ABCD中,AD=BC, AD=5cm,AB=8cm,CF=2cm,∴BF=3cm。 ∵△ABF∽△ECF,∴ 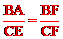 ,即
,即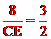 。
。
∴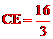 (cm)。
(cm)。
22.(2013年广西百色8分)“中秋节”是我国的传统佳节,历来都有赏月,吃月饼的习俗。小明家吃过晚饭后,小明的母亲在桌子上 放了四个包装纸盒完全一样的月饼,它们分别是2个豆沙,1个莲蓉和1个叉烧。
放了四个包装纸盒完全一样的月饼,它们分别是2个豆沙,1个莲蓉和1个叉烧。
(1)小明随机拿一个月饼,是莲蓉的概率是多少?
(2)小明随机拿2个月饼,请用树形图或列表的方法表示所有可能的结果,并计算出没有拿到豆沙月饼的概率是多少?
【答案】解:
(1)∵共有4个月饼,莲蓉月饼有1个,
∴小明随机拿一个月饼,是莲蓉的概率是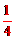 。
。
(2)画树形图如下:
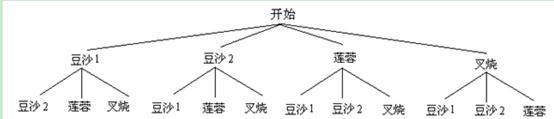
∵共有12种等可能结果,没有拿到豆沙月饼的情况有2种,
∴没有拿到豆沙月饼的概率是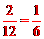 。
。
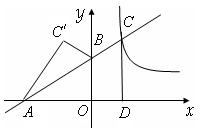
23.(2013年广西百色8分)如图,在平面直角坐 标系xOy中,直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),并与
标系xOy中,直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),并与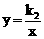 的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。
的图象在第一象限交于点C,CD⊥x轴,垂足为D,OB是△ACD的中位线。
(1)求一次函数与反比例函数的解析式;
(2)若点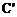 是点C关于y轴的对称点,请求出△
是点C关于y轴的对称点,请求出△ 的面积。
的面积。
【答案】解:
(1)∵直线y=k1x+b交x轴于点A(-3,0),交y轴于点B(0,2),
∴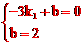 ,解得
,解得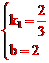 。
。
∴一次函数的解析式为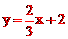 。
。
∵OB是△ACD的中位线,OA=3,OB=2,∴OD=3,DC=4。
∴C(3,4)。
∵点C在双曲线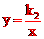 上,∴
上,∴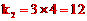 。
。
∴反比例函数的解析式为 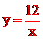 。
。
(2)
∵点 是点C(3,4)关于y轴的对称点,∴
是点C(3,4)关于y轴的对称点,∴ (-3,4)。
(-3,4)。
∴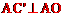 。∴△
。∴△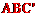 的面积等于梯形
的面积等于梯形 减△
减△ 。
。
∴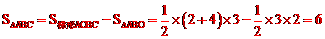 。
。
24.(2013年广西百色10分)为响应区“美丽广西 清洁乡村 ”的号召,某校开展“美丽广西 清洁校园 ”的活动,该校经过精心设计,计算出需要绿化的面 积为498m2,绿化150m2后,为了更快的完成该项绿化工作,将每天的工作量提高为原来的1.2倍。结果一共用20天完成了该项绿化工作。
积为498m2,绿化150m2后,为了更快的完成该项绿化工作,将每天的工作量提高为原来的1.2倍。结果一共用20天完成了该项绿化工作。
(1)该项绿化工作原计划每天完成多少m2?,
(2) 在绿化工作中有一块面积为170m2的矩形场地,矩形的长比宽的2倍少3 m,请问这块矩形场地的长和宽各是多少米?
【答案】解:
(1)设该项绿化工作原计划每天完成xm2,则提高工作量后每天完成1.2xm2,根据题意,得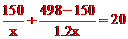 ,解得x=22。经检验,x=22是原方程的根。答:该项绿化工作原计划每天完成22m2。
,解得x=22。经检验,x=22是原方程的根。答:该项绿化工作原计划每天完成22m2。
(2)设矩形宽为y m,则长为2y-3 m,根据题意,得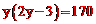 , 解得
, 解得 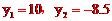 (不合题意,舍去)。2y-3=17。
(不合题意,舍去)。2y-3=17。
答:这块矩形场地的长为17 m,宽为10 m 。
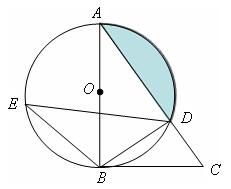
25.(2013年广西百色10分)如图,在△ABC中,以AB为直径的⊙O交AC于点D,直径AB左侧的半圆上有一点动点E(不与点A、B重合),连结EB、ED。
(1)如果∠CBD=∠E,求证:BC是⊙O的切线;
(2)当点E运动到什么位置时,△EDB≌△ABD,并给予证明;
(3)若tanE=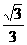 ,BC=
,BC=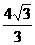 ,求阴影部分的面积。(计算结果精确到0.1)
,求阴影部分的面积。(计算结果精确到0.1)
(参考数值:π≈3.14, 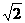 ≈1.41,
≈1.41,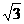 ≈1.73)
≈1.73)
【答案】解:
(1)证明:∵AB为⊙O的直径,∴∠ADB=90°,即∠ABD+∠BAD=90°。
又∵∠CBD=∠E,∠BAD=∠E,∴∠ABD+∠CBD=90°,即∠ADC=90°。
∴BC⊥AB。∴BC是⊙O的切线。
(2)当点E运动到DE经过点O位置时,△EDB≌△ABD。证明如下:
当点E运动到DE经过点O位置时,∠EBD=∠ADB=90°,
又∵∠ABD=∠E,BD=DB,∴△EDB≌△ABD(AAS)。
(3)如图,连接OD,过点O作OF⊥AD于点F,
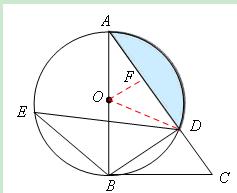
∵∠BAD=∠E,tanE=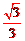 ,∴tan∠BAD=
,∴tan∠BAD=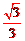 。
。
又∵∠ADB=90°,∴∠BAD=30°。
∵∠ABC=90°,BC=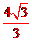 ,∴
,∴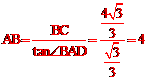 。
。
∴AO=2,OF=1,AF=AOcos∠BAD=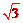 。∴AD=
。∴AD=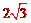 。
。
∵AO=DO,∴∠AOD=120°。
∴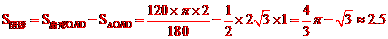 。
。
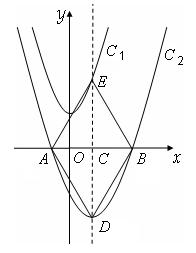
26.(2013年广西百色12分)如图,在平面直角坐标系xOy中,将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2。C2的图象与x轴交于A、B两 点(点A在点B的左侧)。
点(点A在点B的左侧)。
(1)求抛物线C2的解析式;
(2)若抛物线C2的对称轴与x轴交于点C,与抛物线 C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
C2交于点D,与抛物线C1交于点E,连结AD、DB、BE、EA,请证明四边形ADBE是菱形,并计算它的面积;
(3)若点F为对称轴DE上任意一点,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,如果存在,请求出点G的坐标,如果不存在,请说明理由。
【答案】解:
(1)∵将抛物线C1:y=x2+3先向右平移1个单位,再向下平移7个单位得到抛物线C2,
∴抛物线C1的顶点(0,3)向右平移1个单位,再向下平移7个单位得到(1,-4)。
∴抛物线C2的顶点坐标为(1,-4)。
∴抛物线C2的解析式为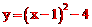 ,即
,即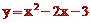 。
。
(2)证明:由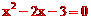 解得
解得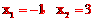 ,
,
∵点A在点B的左侧,∴A(-1,0),B(3,0),AB=4。
∵抛物线C2的对称轴为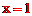 ,顶点坐标D为(1,-4),∴CD=4。AC=CB=2。
,顶点坐标D为(1,-4),∴CD=4。AC=CB=2。
将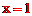 代入y=x2+3得y=4,∴E(1, 4),CE=DE。
代入y=x2+3得y=4,∴E(1, 4),CE=DE。
∴四边形ADBE是平行四边形。
∵ED⊥AB,∴四边形ADBE是菱形。
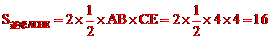 。
。
(3)存在。分AB为平行四边形的边和对角线两种情况:
①当AB为平行四边形的一边时,如图,
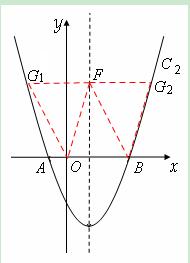
设F(1,y),
∵OB=3,∴G1(-2,y)或G2(4,y)。
∵点G在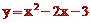 上,
上,
∴将x=-2代入,得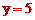 ;将x=4代入,得
;将x=4代入,得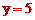 。
。
∴G1(-2,5),G2(4,5)。
②当AB为平行四边形的一对角线时,如图,
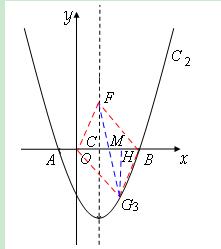
设F(1,y),OB的中点M,过点G作GH⊥OB于点H,
∵OB=3,OC=1,∴OM=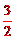 ,CM=
,CM=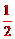 。
。
∵△CFM≌△HGM(AAS),∴HM=CM=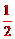 。∴OH=2。
。∴OH=2。
∴G3(2,-y)。
∵点G在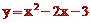 上,
上,
∴将(2,-y)代入,得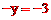 ,即
,即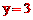 。
。
∴G3(2,-3)。
综上所述,在抛物线C2上是否存在这样的点G,使以O、B、F、G四点为顶点的四边形是平行四边形,点G的坐标为G1(-2,5),G2(4,5),G3(2,-3)。


